
Выч.мат
..pdf
где n – количество отрезков, на которые разбивается отрезок интегрирования.
I = 1∫e−x2 dx .
0
Решение. Максимальные погрешности формул трапеций и Симпсона равны соответственно
R |
= |
|
(b −a)h |
2 |
M |
2 |
, |
|
|
|
R |
C |
= |
(b −a)h4 |
M |
4 |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
T |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
180 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где M 2 = max |
|
f |
′′ |
|
, M 4 = max |
f |
(4) |
(x) |
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
(x) |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Для функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
f (x) = e−x2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−x2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
2 |
−1)e |
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
f (x) = 2(2x |
|
|
|
|
|
|
||||||||||||
Третья производная |
f |
′′′ |
= 4x(3 − x |
2 |
)e |
−x |
2 |
на отрезке [0,1] поло- |
||||||||||||||||||
(x) |
|
|
|
|
|
|||||||||||||||||||||
жительна, т.е. |
|
|
f ′′ – |
возрастающая функция. Следовательно, | f ′′ | |
||||||||||||||||||||||
достигает наибольшего значения на краях интервала, в данном случае
M 2 = f ′′(0) = 2 .
Погрешность формулы трапеций равна
RT = 2 1210 −2 ≈ 0.002 .
Четвертая производная f равна
f (4) = 4(4x4 −12x2 +3)e−x2 .
Экстремумы этой функции, т.е. нули функции
f (5) = 8x(−15 +20x 2 −4x4 )e−x2
лежат вне интервала (0,1). Легко проверить, что M4 = f(4)(0) = 12. Отсюда
RC = 12 10 −4 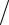 180 = 0.67 10 −5 .
180 = 0.67 10 −5 .
В соответствии с оценками погрешности находим, что в значении интеграла, вычисленным по методу трапеций, третий знак после запятой является сомнительным, а по формуле Симпсона число правильных
41
знаков после запятой не превышает пяти. Вычисление функций в узлах проводим с двумя запасными знаками (шесть знаков после запятой).
i |
0 |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
xi |
0 |
0.1 |
|
|
0.2 |
|
|
0.3 |
|
|
0.4 |
|
|
0.5 |
|
fi |
1 |
0.990050 |
|
0.960789 |
|
0.913931 |
|
0.852144 |
|
0.778801 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
i |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
||||
xi |
|
0.6 |
|
0.7 |
|
0.8 |
|
0.9 |
|
1.0 |
|
||||
fi |
0.697676 |
|
0.612626 |
|
0.527292 |
|
0.444858 |
|
0.367879 |
|
|||||
Вычисление по формуле трапеций (6) с данными из таблицы дает значение интеграла I = 0.7462106, однако с учетом погрешности | R| < 0.002 значение интеграла следует положить равным I = 0.746.
Аналогичные вычисления по формуле Симпсона (8) дают значение интеграла I = 0.7468248. Поскольку погрешность в данном случае составляет | R | < 0.67 10 − 5, то интеграл равен I = 0.74682.
4. Выбор шага интегрирования по оценке остаточного члена
В подобных задачах требуется определить шаг сетки, который обеспечивает требуемую точность ε вычисления интеграла по выбранной квадратурной формуле. Шаг выбирается из условия равенства максимальной погрешности Rmax и заданной точности для данной формулы численного интегрирования
Rmax (h) = ε , |
Rmax = max |
|
R |
|
, |
(10) |
|
|
|||||
|
x |
|
|
|
|
|
где остаточный член R определяется одним из условий (5), (7), (9) соответствующей квадратурной формулы. Тогда для формулы
средних (прямоугольников), трапеций и Симпсона |
получаем сле- |
||||||||||||||||||||||||||||||
дующие выражения Rmax |
соответственно: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
(b −a)h 2 |
|
|
|
|
|
|
|
(b −a)h 2 |
|
|
|
|
|
(b −a)h4 |
|
|
(11) |
|||||||||||
R |
cp |
= |
|
|
|
M |
2 |
, |
|
R |
|
= |
|
|
|
|
|
|
|
M |
2 |
, |
R |
C |
= |
|
|
M |
4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
24 |
|
|
|
|
T |
|
|
|
12 |
|
|
|
|
|
|
|
|
180 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
M 2 |
= max |
|
′′ |
|
|
, |
M 4 |
= max |
f |
(4) |
(x) |
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
f (x) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пример 2. Вычислить интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
π / 2 |
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
I = ∫ |
|
dx |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
π / 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
по формуле трапеций с точностью ε = 10 − 4, определяя шаг h по оценке остаточного члена.
Решение. Величину шага интегрирования определим из соотношения (10) с максимальной погрешностью RT , соответствующей формуле трапеций. Для функции
42
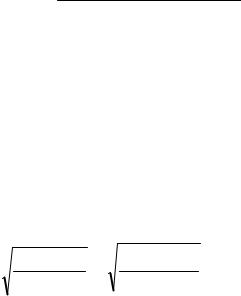
f (x) = |
sin x |
, |
π |
≤ x ≤ |
π |
|
x |
4 |
2 |
||||
|
|
|
имеем
f′′(x) = (2 − x 2 ) sin x − 2x cos x .
x3
Используя представления в виде отрезка ряда
sin x = x − |
|
x3 |
+ |
x5 |
− |
x7 |
, |
|
cos x = 1 − |
|
x2 |
+ |
x4 |
− |
x6 |
||||
|
3! |
5! |
7! |
|
2! |
4! |
6! |
||||||||||||
можем записать |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
x2 |
|
x4 |
|
|
|
|
|
|
||
|
|
|
f |
′′ |
|
≈ F(x) = − |
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
+ |
10 − |
168 |
|
|
|
|
|
|
||||||
|
|
|
(x) |
|
|
|
|
|
|
||||||||||
Экстремумы функции F(x) лежат за пределами отрезка интегрирова-
ния; т.к. f ′′ (π/2) = − 0.121 и f ′′ (π/4) = − 0.274 , то M2 = 0.274.
h = |
12ε |
= |
12 10−4 4 |
= 7.47 10−2 |
|
M 2 (b − a) |
|
0.274 π |
|
В результате (b-a)/h = 10.5, и, следовательно, интервал интегрирования следует разбить на n = 11 отрезков.
Составляем таблицу значений функции в узлах с шагом h = π /44.
i |
0 |
|
1 |
|
2 |
|
3 |
|
|
4 |
|
|
5 |
|
||||||
xi |
|
π |
|
3π |
|
13π |
7π |
|
15π |
|
4π |
|||||||||
|
4 |
|
|
11 |
|
|
44 |
|
|
22 |
|
|
|
44 |
|
|
|
11 |
|
|
fi |
0.900316 |
0.882063 |
0.862468 |
0.841592 |
0.819497 |
0.796248 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
i |
6 |
|
7 |
|
8 |
|
9 |
|
|
10 |
|
|
11 |
|
||||||
xi |
|
17π |
|
9π |
|
19π |
|
5π |
|
21π |
|
π |
||||||||
|
|
44 |
|
|
22 |
|
|
44 |
|
|
11 |
|
|
|
44 |
|
|
2 |
|
|
fi |
0.771916 |
0.746573 |
0.720293 |
0.693154 |
0.665236 |
0.636620 |
||||||||||||||
Вычисление по формуле (6) с данными из таблицы дает значение интеграла I = 0.611719. С заданной точностью I = 0.6117.
5. Процедура двойного пересчета (правило Рунге)
Оценка максимальной погрешности Rmax часто связана с выполнением громоздких вычислений, поэтому на практике используется процедура двойного пересчета. Величина интеграла I рассчитывается сначала с шагом h (n интервалов), затем на сетке с вдвое меньшим шагом h/2 (2n интервалов). Здесь роль погрешности метода вычислений играет величина
∆ = |
|
I 2n − I n |
|
. |
(12) |
|
|
43
Более точные оценки погрешности дают формулы Рунге выбранной квадратурной формулы:
∆ = |
|
1 |
|
I 2n − I n |
|
|
(13) |
|||
|
|
|
||||||||
3 |
||||||||||
|
|
|
|
|
|
|
|
|||
для формулы средних и трапеций, и |
|
|
|
|||||||
∆ = |
|
1 |
|
I 2n − I n |
|
|
(14) |
|||
|
|
|
|
|||||||
|
|
|
|
|||||||
15 |
|
|
|
|
|
|
||||
для формулы Симпсона.
Если ∆ не превосходит заданной погрешности ε, т.е. ∆ < ε, то вычисления прекращают и полагают
I ≈ I 2n .
Если точность вычислений не достигается, то процедуру уменьшения шага повторяют вновь.
Поскольку в данном случае априорная погрешность метода неизвестна, то невозможно использовать выражения (11). Однако, согласно этим соотношениям, погрешность имеет вид для формулы средних и трапеций R = a h2, а для формулы Симпсона R = b h4, где a и b – константы. Следовательно, шаг определяется соотношением h = const
k ε , где k = 2 или k = 4 в зависимости от метода вычисления. На практике константу полагают равной единице, и в качестве начального
шага выбирается величина ε для формул трапеций и средних, и 4 ε
ε для формул трапеций и средних, и 4 ε
для формулы Симпсона. Если точность вычисления интеграла невысока, то в качестве начальной сетки выбирают разбиение на 8 – 10 отрезков.
Пример 3. Используя процедуру двойного пересчета, вычислить по формуле Симпсона интеграл
π |
|
x |
|
|
I = ∫ |
|
dx |
||
1 |
+sin x |
|||
0 |
|
|||
|
|
|
с точностью ε = 2 10 − 4.
Решение. Вначале отрезок интегрирования разбиваем на 8 частей и вычисляем интеграл при h = π/8. Значения аргументов и подынтегральной функции приведены в таблице:
i |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
xi |
0 |
π |
π |
3π |
π |
5π |
|
3π |
7π |
π |
|
8 |
4 |
8 |
2 |
8 |
4 |
8 |
|||
|
|
|
||||||||
fi |
0 |
0.284012 |
0.460075 |
0.612355 |
0.785398 |
1.020591 |
1.380226 |
1.988086 |
π |
|
44
По формуле Симпсона вычисляем значение интеграла при h = π/8 (n=8): I8 = 3.143317. Из этой же таблицы находим значение интеграла при h = π/4 (n=4): I4 = 3.160861. По формуле (12) находим, что раз-
ность
| I8 –I4| = 0.016 > ε = 2 10 − 4
Погрешность ∆, вычисленная по формуле Рунге (14), также превышает ε. Поэтому вычисления следует выполнить с вдвое меньшим шагом h = π /16 (n=16). Результаты вычисления аргумента и функции сводим в следующую таблицу:
|
i |
|
0 |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
|||||||||||||||||
|
xi |
|
0 |
|
|
|
π |
|
|
|
π |
|
|
3π |
|
|
π |
|
|
|
5π |
|
|
|
|
3π |
|
|
|
7π |
|
|
|||||||||||
|
|
|
16 |
|
|
8 |
|
|
|
16 |
|
|
4 |
|
|
16 |
|
|
|
|
8 |
|
|
|
|
16 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
fi |
|
0 |
0.164296 |
0.284012 |
|
0.378671 |
|
0.460075 |
|
0.536043 |
|
0.612355 |
|
0.693889 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
8 |
|
9 |
|
|
|
10 |
|
|
11 |
|
|
12 |
|
13 |
|
|
|
14 |
|
|
15 |
|
|
|
16 |
|
|||||||||||||||
|
|
π |
|
|
|
9π |
|
|
|
5π |
|
|
|
11π |
|
|
|
3π |
|
|
|
13π |
|
|
|
7π |
|
|
15π |
|
π |
|
|||||||||||
|
|
2 |
|
|
16 |
|
|
|
8 |
|
|
|
16 |
|
|
|
4 |
|
|
16 |
|
|
|
|
8 |
|
|
|
|
16 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
0.785398 |
|
0.892144 |
|
1.020591 |
|
1.179296 |
|
1.380226 |
1.640905 |
|
1.988086 |
|
2.464452 |
|
π |
|
||||||||||||||||||||||||||
|
Значение |
интеграла, вычисленное по этой таблице, равно I16=3.141716. |
|
|
|||||||||||||||||||||||||||||||||||||||
|
Разность | I16 –I8|=0.0016. Согласно соотношению (14) погрешность |
|
|
||||||||||||||||||||||||||||||||||||||||
∆ = |
|
I16 − I 8 |
|
|
= 10 −4 < ε . |
|
|
||||
|
|
||||
15 |
|
|
|||
|
|
|
|
||
Следовательно, значение интеграла I = I16 =3.1417.
6. Интегрирование с помощью степенных рядов
Пусть подынтегральная функция f(x) разлагается в степенной ряд
f (x)= ∑∞ Ck xk ,
k=0
сходящийся в интервале –R ≤ x ≤ R, который содержит отрезок интегрирования [a, b]. Тогда функцию можно почленно интегрировать
b∫ f (x)dx = ∑∞ |
Ck |
|
(bk +1 |
− ak+1 ). |
|
|
|
||||
a |
k =0 k + |
1 |
|
|
|
Если ряд сходится быстро, то его можно заменить частной суммой
b∫ f (x)dx ≈ ∑N |
Ck |
|
(bk +1 |
− ak+1 ). |
|
|
|
||||
a |
k =0 k + |
1 |
|
|
|
45

В данном случае, погрешность складывается из погрешности округления членов суммы и погрешности обрезания ряда, равной остатку ряда. Для знакопеременного ряда абсолютная величина остатка ряда не превосходит абсолютной величины первого отброшенного члена ряда. В других случаях используют мажорантные оценки известными рядами.
Пример 4. Вычислить интеграл
I =π∫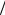 4 sin (x2 )dx
4 sin (x2 )dx
0
с точностью ε = 10 − 4 путем разложения подынтегральной функции в ряд. Оценить количество слагаемых в приближенном выражении интеграла по формуле трапеций с той же точностью
Решение. Для функции |
f = sin x2 имеем разложение |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
sin x2 = x2 − |
|
x6 |
+ |
|
x10 |
|
− |
x14 |
|
+… |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
5! |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
7! |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Интегрирование почленно дает |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
3 |
|
|
|
|
|
7 |
|
|
|
|
|
11 |
x3 |
|
x7 |
|
x11 |
|
x |
15 4 |
|
1 |
π |
|
|
|
1 π |
1 |
|
π |
|
||||||||||||||
I = |
|
− |
|
|
+ |
|
|
|
− |
|
|
|
|
= |
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
−… |
|
7 3! |
11 |
5! |
|
|
|
3 |
|
7 |
|
11 |
|
4 |
|||||||||||||||||||
3 |
|
|
|
15 7! |
|
|
4 |
|
3! 4 |
|
5! |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку ряд знакопеременный, то достаточно удержать столько членов, чтобы первый отброшенный был менее 10 − 4. Этому условию удовлетворяет третье слагаемое, поскольку
|
|
|
|
|
|
π 11 |
|
= |
(0,786)11 |
= |
|
0,051 |
< 4 10 −5 . |
|
|||||
|
|
|
|
11 5! 411 |
|
1320 |
1320 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Следовательно, интеграл равен |
|
|
|
|
(0,78540)4 |
|
|
||||||||||||
|
π 3 |
|
|
|
|
π7 |
|
|
1 |
(0,78540)3 |
|
|
|
=0,1571 . |
|||||
I = |
|
|
− |
|
|
= |
|
|
1 |
− |
|
|
|
||||||
3 4 |
3 |
|
3! 47 |
3 |
|
14 |
|||||||||||||
|
7 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Погрешность формулы трапеций определяется формулой (11). Макси-
2 |
2 |
2 |
мум функции f ′′ =2cosx |
−4x sinx находим из условия экстремума |
|
f ′′′=−12xsinx2 −8x3 cosx2 =0.
Уравнение
tgx2 = − 23 x2
46

имеет единственное решение x=0 и оно соответствует максимуму f ′′. По формуле (11) находим
R = π h2 2 =10−4 . 4 12
Следовательно, шаг h ~ 3 10−2 =0,03 , т.е. для достижения указан-
ной точности по формуле трапеций следует взять около 30 слагаемых.
Задачи
1.Определить погрешность составных формул прямоугольников
(2) и (3).
2.Определить погрешность квадратурных формул:
a) |
4h |
4h |
(2 f1 − f2 + 2 f3 ) по элементарному промежутку |
∫ f (x) dx = |
|||
|
0 |
3 |
|
|
|
|
|
с точками x0 = 0 , |
x1 = h , x2 = 2h , x3 = 3h , x4 = 4h ; |
||
b) |
3h |
3h |
( f0 + 3 f1 + 3 f2 + f3 ) по элементарному проме- |
∫ f (x) dx = |
|||
|
0 |
8 |
|
|
|
|
|
жутку с точками x0 = 0 , x1 = h , x2 = 2h , x3 = 3h .
3. Определить погрешность составной квадратурной формулы
x |
|
1 |
|
|
1 |
|
h2 |
|
|
∫n |
f (x) dx = h ( |
f0 + f1 + f2 +... + |
fn + |
fn ) − |
( fn′ − f0′) |
||||
2 |
2 |
|
|||||||
x0 |
|
|
|
12 |
|
||||
|
|
|
f ′− производная. |
||||||
на равномерной сетке с n+1 узлами, |
|||||||||
4. Вычислить интегралы по формуле средних при n = 10, где n – количество отрезков, на которые разбивается отрезок интегрирования и оценить погрешность вычислений.
a) |
π / 2 |
sin x |
|
dx ; |
b) |
1 |
|
dx |
|
; |
|||
∫ |
|
|
|
|
∫ |
|
|
|
|
||||
|
1 + x2 |
1 + cos3 |
|
||||||||||
|
0 |
|
|
|
0 |
x |
|||||||
c) |
1 |
|
dx |
; |
|
d) |
1 |
|
dx |
. |
|
|
|
∫ |
|
|
|
|
∫ |
|
|
|
|
||||
1 + e x |
|
|
|
|
|
||||||||
|
0 |
|
|
|
0 ch x |
|
|
|
|||||
5. Вычислить интегралы по формуле трапеций (n = 10) и формуле Симпсона (n = 10) и оценить погрешность вычислений, где n – количество отрезков, на которые разбивается отрезок интегрирования.
47
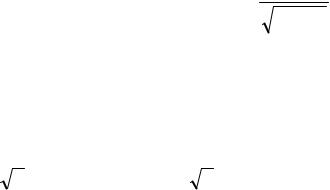
1 |
2 dx ; |
1 |
1 |
a) I = ∫e−x |
b) I = ∫sin x2 dx ; |
c) I = ∫cos x2 dx . |
|
0 |
|
0 |
0 |
6. Вычислить интегралы по формуле трапеций с точностью ε, определяя шаг h по оценке остаточного члена:
1 |
|
|
|
dx |
, ε = 10 −2 |
1 |
dx |
, ε = 10 −3 ; |
a) I = ∫ |
|
|
|
; b) I = ∫ |
||||
|
1 + x2 |
1 + x2 |
||||||
0 |
|
|
0 |
|
||||
π / |
2 |
sin x dx, ε =10 |
−4 . |
|
|
|||
c) I = |
∫ |
|
|
|
||||
π |
/ 4 |
x |
|
|
|
|
||
|
|
|
|
|
||||
7. Вычислить интегралы по формуле Симпсона с точностью ε=10 – 3 используя процедуру двойного пересчета.
1 |
1 |
π |
dx |
|
|
a) I = ∫ x sin xdx , |
b) I = ∫ x cos xdx , |
c) I = ∫ |
|
. |
|
1 + sin 3 |
|
||||
0 |
0 |
0 |
x |
||
8. Вычислить интеграл с точностью ε, разлагая подынтегральную функцию в степенной ряд.
|
2 |
|
sin x |
|
ε = 10 −5 |
π |
sin x |
|
−3 |
|
||
a) |
I = ∫ |
dx, |
; b) I = ∫ |
dx, ε = 10 |
; |
|||||||
|
|
|||||||||||
|
0 |
|
x |
|
|
|
0 |
x |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
2 dx, |
|
|
|
|
|
|
|||
c) |
I = ∫e−x |
ε = 10 −4 . |
|
|
|
|
||||||
|
|
0 |
|
|
|
|
|
|
|
|
||
9. Сколько слагаемых следует взять в разложении подынтегральной функции, чтобы вычислить интеграл
I =π∫e−x2 dx,
0
с точностью ε =10−4 .
10. Вычислить по формуле трапеций интеграл:
1 |
|
|
− x, |
−1 ≤ x ≤0 |
|
I = ∫ f (x)dx, |
f (x) = |
x |
= |
x, |
0 ≤ x ≤1 |
−1 |
|
|
|
||
при четном и нечетном количестве узлов равномерной сетки. 11. Каким образом следует выбрать узлы сетки, чтобы интеграл
2 |
x + 1, |
0 ≤ x ≤1 |
||
I = ∫ f (x)dx, |
|
|
|
|
f (x) = |
2 |
|
|
|
0 |
|
− 2x + 2, |
1 ≤ x ≤ 2 |
|
x |
|
|||
48
вычисленный по формуле Симпсона имел наименьшую погрешность.
12. Вычислить интеграл, заданный таблицей, и оценить погрешность:
i |
0 |
1 |
|
2 |
|
3 |
|
|
4 |
5 |
6 |
|
7 |
8 |
|||
xi |
1 |
1.2 |
1.4 |
|
1.6 |
|
1.8 |
2.0 |
2.2 |
|
2.4 |
2.6 |
|||||
fi |
0.5 |
0.5455 |
0.5833 |
|
0.6154 |
|
0.6429 |
0.6667 |
0.6875 |
|
0.7059 |
0.7222 |
|||||
Ответы и указания. |
|
|
|
|
|
|
(xn − x0 ) |
|
|
|
|
||||||
2a) |
|
14 |
h5 f (4) (ξ) , |
2b) − |
3 |
h5 f |
(4) (ξ) , 3) |
h4 f (4) |
(ξ) ; |
|
|||||||
45 |
80 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
720 |
|
|
|
|
||||
5a). I = 0.746, | R | < 0.002 ; I = 0.74682, | R | < 0.67 10 –5; |
|
|
|
||||||||||||||
5b). I = 0.311, | R | < 1.9 10 -3 ; I = 0.3103, | R | < 1.6 10 -5 ; |
|
|
|
||||||||||||||
5c). I = 0.903, | R | < 3.2 10 -3 ; I = 0.9045, | R | < 1.3 10 –5; |
|
|
|
||||||||||||||
6a). I = 0.78 ; |
6b). I = 0.88137 ; |
6c). I = 0.6118; |
|
|
|
|
|||||||||||
7a). I = 0.364 ; |
7b). I = 0.531 ; |
7c). I = 2.353 ; |
|
|
|
|
|||||||||||
8a). I = 1.60543 ; |
8b). I = 1.852 ; |
|
8c). I = 0.7468 ; |
|
|
|
|
||||||||||
10). I = 1, n = 2k; I = 1+1/n2, n = 2k +1 ;
11). Учесть, что формула Симпсона является точной для кубических многочленов.
VI. Решение алгебраических и трансцендентных уравнений
Рассмотрим итерационные методы решения уравнения
f (x)= 0 , |
(1) |
где f(x) − непрерывная функция. Необходимо учитывать, что это уравнение может иметь несколько корней, среди которых могут быть кратные, корни могут быть как действительные, так и комплексные. При определении только действительных корней вначале определяется область x существования корней. Эту процедуру удобно выполнять с помощью графика y = f (x) или таблицы этой
функции. Корням соответствуют точки x, в которых f(x) либо касается оси x (кратный корень четной кратности), либо пересекает ось x (простой корень или кратный корень нечетной кратности). В последнем случае функция f(x) имеет разные знаки в близких точках, расположенных слева и справа от корня.
1. Метод деления отрезка пополам
Суть этого итерационного метода заключается в следующем (рис.10). Пусть имеются точки x0 и x1, в которых f(x) имеет разные знаки f(x0) <0 f(x1) >0 , т.е. на отрезке [x0 , x1] имеется по крайней мере один корень. Определяем середину отрезка x2 = (x0 + x1)/2 и вычисляем f(x2). Из двух половин отрезка выбираем ту, для кото-
49

рой f(x2) f(xгран) ≤ 0, поскольку корень лежит на этой половине. Здесь xгран есть x0 или x1. Новый отрезок делится пополам (точка x3) и выбирается та половина, на которой f(x) имеет разные знаки на
концах отрезка.
x0 |
x2 |
x3 |
x |
|
|
|
x1 |
|
f(x) |
|
|
|
Рис.10 |
|
|
Счет прекращается, когда разность соседних итераций не превыша-
ет требуемой погрешности: | xn+1 – xn| < ε.
2. Метод простых итераций
Рассмотрим вместо уравнения (1) эквивалентное ему |
|
x = ϕ(x). |
(2) |
Переход к этому уравнению можно сделать различными способами. Например, путем x = x + f (x). Здесьϕ(x)= x + f (x). Другим
способом выражения функции может быть ϕ(x)= x +ψ(x)f (x), где ψ(x)− непрерывная функция, которая должна быть знакопостоян-
ной, чтобы не привнести дополнительные корни. Выберем некоторое x0 и на основе (2) построим итерационный процесс
xn+1 = ϕ(xn ), |
(3) |
где n =0,1,2,… Условием сходимости итерационного процесса (3) является неравенство
′ |
, |
(4) |
ϕ (x) ≤ q < 1 |
которое должно выполняться в некоторой окрестности корня x . Тогда последовательность {xn }сходится при любом начальном x0,
если на отрезке [x0 , x]производная ϕ′(x) <1 . В данном методе
близость n-го приближения к корню x оценивается следующей цепочкой неравенств
| xn − x | ≤ 1 −q q | xn − xn−1 | ≤ ε .
50
