
Выч.мат
..pdf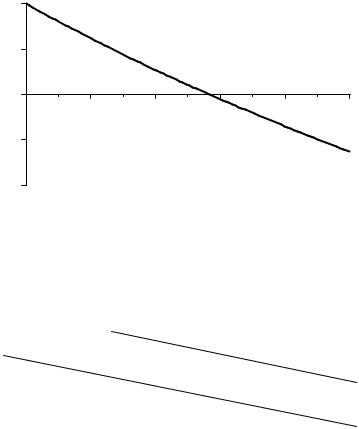
тех пор, пока n-ое приближение x (n) = g(x точности совпадет с x (n-1).
Пример 6. Решить уравнение
f (x)≡ e−x − x = 0 .
(n-1)) в пределах заданной
(9)
Решение. Ориентировочное значение корня определяем графически.
1,0 |
|
|
|
|
|
0,5 |
f(x)= e - x - x |
|
|
||
0,0 |
|
|
|
x |
|
0,4 |
0,6 |
0,8 |
1,0 |
||
0,2 |
|||||
-0,5 |
|
|
|
|
|
-1,0 |
|
|
|
|
|
|
Рис. 4 |
|
|
|
|
Как видно из графика (рис.4) решение одно и лежит в районе x~0.5-0.6. В качестве узлов берем fi , в качестве функций − xi. Составим интерполяционную таблицу для xi = 0.5; 0.55 и 0.6.
fi |
xi |
|
x(1) |
|
x (2) |
|
0,106531 |
0,5 |
|
-0,628291 |
|
|
|
0,026950 |
0,55 |
|
|
0,073557 |
|
|
|
-0,639894 |
|
|
|||
- 0,051188 |
0,6 |
|
|
|
|
|
|
|
|
|
|
||
Тогда с помощью многочлена Ньютона (7) имеем |
||||||
x(f )≈ Ln (f )= x0 +(f − f0 )(−0,628291)+(f − f0 )(f − f1 ) 0,073557 |
||||||
Решению уравнения (9) |
соответствует такое x |
, при котором f = 0. |
||||
Следовательно x(0) ≈ 0,5 + ( - 0,106531) ( - 0,628291) + ( - 0,106531) ( -0,026950) 0,073557 = 0,567143.
Оценку погрешности проведем путем сравнения результатов на разных сетках узлов. Введем в таблицу узел x = 0.65:
fi |
xi |
x(1) |
x (2) |
x(3) |
|
0,106531 |
0,5 |
-0,628291 |
|
|
|
0,026950 |
0,55 |
0,073557 |
|
||
-0,639894 |
|
||||
- 0,051188 |
0,6 |
0,073387 |
0,000725 |
||
-0,651262 |
|||||
- 0,127954 |
0,65 |
|
|
||
|
|
|
21

Добавление нового узла приводит только к добавлению в верхнюю диагональ таблицы третьей разделенной разности. Следовательно, скорректированное значение корня будет равно:
x(0) ≈ 0,567143+ ( - 0,106531) ( -0,026950) (0,051180) (0,000725) = 0,567143+ 1.06 10 − 7.
По результатам вычислений можем положить, что корень уравнения
(9) равен x = 0,56714, поскольку в шестом знаке проводилось округление.
Пример 7. С точностью 10 − 4 найти корень алгебраического уравнения
|
x 4 |
− 3 x + 1 = 0 |
, |
|
|
расположенный в промежутке 0 < x < 1. |
|
|
|
||
Решение. Составляем таблицу разностей с шагом 0.1: |
|
||||
xi |
fi |
f(1) |
f (2) |
f(3) |
f(4) |
0.10.7001
0.2 |
- 2,985 |
|
|
0.4016 |
0,25 |
|
|
0.3 |
- 2,935 |
|
1 |
0.1081 |
0.55 |
1 |
|
0.4 |
- 2.825 |
|
1.4 |
- 0.1744 |
0.97 |
1 |
|
0.5 |
- 2.631 |
|
1.8 |
- 0.4375 |
1.51 |
|
|
|
- 2.329 |
|
|
0.6-0.6704
Из таблицы видно, что корень расположен в промежутке 0.3 < x < 0.4. Интерполяционный многочлен (6) равен:
f(x) = 0.7001 – 2.985 (x - 0.1) + 0.25 (x - 0.1)(x - 0.2) + (x – 0.1)
(x - 0.2)(x - 0.3) + (x – 0.1) (x - 0.2)(x - 0.3)(x – 0.4).
Полагаем в этом равенстве f = 0 и преобразуем к эквивалентному виду:
x = |
0.9986 |
+ |
0.25 |
(x −0.1)(x −0.2) + |
(x −0.1)(x −0.2)(x −0.3) |
+ |
||
2.985 |
|
2.985 |
2.985 |
|||||
|
|
|
|
|
||||
|
+ |
(x −0.1)(x −0.2)(x −0.3)(x −0.4) |
. |
(10) |
||||
|
|
|||||||
|
|
|
|
|
2.985 |
|
|
|
В качестве начального приближения выбираем x(0) =0.9986/2.985 = 0.334539. Значение следующего приближения x(1) = 0.337523 определяем, подставив x(0) в правую часть соотношения (10). После-
дующие приближения дают x(2) = 0.337666, x(3) = 0.3376664, x(4) =
22

0.3376667. Из сравнения результатов видим, что уже второе приближение дает значение корня x = 0.3377 с требуемой точностью.
5. Интерполяция сплайнами
Основная идея этого метода заключается в том, чтобы интерполяцию проводить не на всем промежутке [x0 , xN ] как в лагранжевой интерполяции, а на каждом интервале [xi , xi+1].Таким образом, в сплайновой интерполяции единая кривая получается как совокупность отдельных кусочков кривых на каждом промежутке. В узлах функция принимает заданные значения. В сплайновой интерполяции условие несовпадения узлов не является обязательным (различны только соседние узлы), и с помощью сплайнов можно интерполировать многозначные функции.
f |
|
f7 |
f6 |
|
|
|
|
|
|
|
|||
f9 |
f8 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
f5 |
|
|
|
f |
f2 |
f |
f4 |
|
|
|
1 |
|
3 |
|
|
|
f0 |
x8 |
x7 |
x6 |
x5 |
|
|
x9 |
x |
|||||
x0 |
x1 |
x2 |
x3 |
x4 |
||
|
Рис.5
5.1.При линейной сплайновой интерполяции на каждом отрезке функ-
ция аппроксимируется прямой линией, причем в узлах она принимает заданные значения. Очевидно, что графиком такой функции на всем промежутке [x0 , xN ] будет ломаная прямая (рис.5).
5.2.Интерполяция квадратичными сплайнами. На оси x задается система узлов {xi}, в которых заданы значения функции {fi}, 0≤ i ≤ N. На каждом отрезке [xi , xi+1] между соседними узлами функция представляется отрезком параболы
ϕ(x)= a |
i |
+ b (x − x |
i−1 |
)+ c |
(x − x |
i−1 |
)2 |
, |
1≤ i ≤ N . |
(11) |
|
i |
i |
|
|
|
|
|
Для определения коэффициентов ai, bi, ci используются условия равенства функций f и ϕ во всех узлах, а также непрерывности производной функции ϕ во внутренних узлах, которые приводят к сис-
23
теме 3N−1 линейных алгебраических уравнений относительно 3N неизвестных
ai = fi−1 |
|
1 ≤ i ≤ N |
(12) |
|
|
|
+ ci hi2 = fi |
1 ≤ i ≤ N |
(13) |
ai + bi hi |
||||
|
= bi |
+ 2ci hi |
1 ≤ i ≤ N − 1 |
(14) |
bi+1 |
||||
|
|
|
|
|
Здесь hi = x i – x i -1 . Для замыкания системы уравнений используется дополнительное условие, например, «свободного» конца кривой:
ϕ′(x0 ) = 0 , ( или ϕ′(xN ) = 0 ) . |
(15) |
Уравнение (12) определяет коэффициенты ai, из (13) находим связь bi, ci:
b |
= −c h + |
fi+1 − fi |
, |
1 ≤ i ≤ N , |
(16) |
|
|||||
i |
i i |
hi |
|
|
|
|
|
|
|
|
а комбинация уравнений (14) – (16) дает систему уравнений для определения ci:
c |
h |
+ c h |
= |
fi+1 − fi |
− |
fi − fi−1 |
1 ≤ i ≤ N −1 |
|
|
|
|
|
|||||||
|
i+1 i+1 |
i i |
hi+1 |
|
|
hi |
|
|
|
|
|
|
|
|
|
|
|
||
b1 + 2c1h1 =0 , |
|
или |
bN + 2cN hN =0 . |
(17) |
|||||
Система уравнений (12), (16), (17) однозначно определяет коэффициенты квадратичного сплайна (11).
Пример 8. Построить квадратичный сплайн функции f, заданной таблицей
x0 = − 1 |
x1 = 0 |
x2 = 1 |
x3 = 0 |
f0 = 0 |
f1 = 1 |
f2 = 0 |
f3 = − 1 |
с дополнительным условием
f ′(x3 ) =0 .
Построить график интерполирующей функции.
Решение. В данном случае сетка не является равномерной, поскольку шаг не равен единой константе для всех промежутков:
h 1 = 1, h 2 = 1, h 3 = − 1. Системы уравнений (16) и (17) имеют вид:
b1 + c1 = 1 |
c1 + c2 = − 2 |
b2 + c2 = − 1 |
c2 − c2 = 2 |
b3 − c3 = 1 |
b3 − 2 c3 = 0 |
Из этих уравнений находим b1 =6, b2 =− 4, b3 =2, с1 =1, с2 =3, с3 =1. Соотношение (12) определяет константы ai: a1 =0, a2 =1, a3 =0.
24

Подставляя константы в (11), находим интерполирующую функ- |
|||||||
цию: |
|
|
|
|
|
|
|
ϕ1 (x) = 0 + 6 (x + 1) − 5 (x + 1) 2 = − 5 x 2 − 4 x + 1 |
|||||||
ϕ2 (x) = 1 − 4 x + 3 x 2 |
|
|
|
|
|
|
|
ϕ3 (x) = 0 + 2 (x − 1) + (x − 1) 2 = x 2 − 1. |
|
||||||
На рис. 6 приведен график функции ϕ (x). |
|
||||||
|
|
|
|
|
f |
|
|
|
ϕ1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ϕ2 |
x |
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
0 |
|
1 |
|
|
|
-1 |
ϕ3 |
|||
Задачи |
|
Рис.6 |
|
|
|||
|
|
|
|
|
|
|
|
В задачах 1 – 3 индексированная переменная xi |
означает координату |
||||||
одного из узлов. |
|
|
|
|
|
|
|
1. Доказать, что |
|
|
|
|
|
|
|
a) ωk−1 (xk ) =ω 'k (xk ) ; |
b) (xi − xk )ω 'k −1 (xi ) =ω 'k (xi ) |
||||||
где |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωn (x) = ∏(x − x j ) . |
|
|
|
|
|||
|
j=0 |
|
|
|
|
|
|
2. Доказать, что |
|
|
|
|
), |
|
|
ωn (x) |
|
ω′ |
(x |
i |
m = i |
|
|
|
= n |
|
|
|
|
||
x − x |
|
|
|
|
|
m ≠ i |
|
m x=x |
0, |
|
|
|
|
||
3. Доказать, что |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d ωn2 (x) |
|
|
=ω 'n (xi )ω ' 'n (xi ) . |
|||
|
|
|
|
|
||
dx (x − xi ) |
2 |
|||||
|
x=xi |
|||||
|
|
|
|
|
||
25
4. Какова наибольшая погрешность линейной интерполяции для следующих таблиц функций:
a)таблица косинусов с шагом 1°;
b)таблица натуральных логарифмов в диапазоне аргументов от 1 до 10 с шагом 0.001?
5.Определить наибольшую погрешность квадратичной интерполяции функции f(x) на равномерной сетке с шагом h.
6.Определить шаг четырехзначной таблицы ( ε = 5 10−5 ) функции
f(x) для квадратичной интерполяции на всем отрезке [0, π/2].
|
|
|
a) f (x) = sin x |
b) f (x) = cos x . |
|
|
|
|
|||||
7. |
По вычисленным значениям sin x при x = |
0 , |
π |
, |
π |
, |
π |
, |
π |
, найти |
|||
|
|
π |
|
|
|
6 |
|
4 |
|
3 |
|
2 |
|
sin |
и определить погрешность. |
|
|
|
|
|
|
|
|
|
|
||
12 |
|
|
π |
|
π |
|
π |
|
π |
|
|||
|
|
|
|
|
|
|
|
|
|||||
8. |
По вычисленным значениям cos x при x = |
0 , |
, |
, |
, |
, найти |
|||||||
|
|
π |
|
|
|
6 |
|
4 |
|
3 |
|
2 |
|
cos |
и определить погрешность. |
|
|
|
|
|
|
|
|
|
|
||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
9. Методом обратного интерполирования найти корень уравнения:
a) |
x2 |
+ ln x = 0 |
с точностью 10 − 4 в промежутке [0.5 ; 1]; |
|
b) |
x2 |
− lg (x + 2) = 0 с точностью 10 − 4 |
в промежутке [0.5 ; 1]; |
|
c) |
x2 |
+ ln x − 4 = 0 |
с точностью 10 − 4 |
в промежутке [1.5 ; 2]. |
10. Методом обратного интерполирования с точностью до 10 − 4 найти корень алгебраического уравнения:
a) x4 + 3x3 − 9x – 9 = 0 |
1 ≤ x ≤ 2 |
b) x4 − 4x3 + 4x2 – 4 = 0 |
– 1 ≤ x ≤ 0 |
c) x4 + 3x3 + 4x2 + x – 3 = 0 |
0 ≤ x ≤ 1 |
d) x4 − 3x3 + 4x2 + x – 3 = 0 |
– 1 ≤ x ≤ 0 |
11. Провести численную интерполяцию квадратичными сплайнами функции f , заданной в точках x0 , x1 , x2 , x3, с дополнительным условием на производную. Построить график интерполирующей функции.
а) x0 = −1, x1 = 0, x2= 1; |
f(x0)= 0, |
f(x1)= −1, f(x2)= 0; |
f′(x0)= 0; |
|||
b) x0 = −1, |
x1 = 0, |
x2= 1; |
f(x0)= 0, |
f(x1)= 1, |
f(x2)= 0; |
f′(x0)= −1; |
c) x0 =−1, |
x1 = 0, |
x2= 1; |
f(x0)= 0, |
f(x1)= 1, |
f(x2)= 0; |
f′(x2)= −1; |
26

d) x0 = 0, |
x1 = 1, |
x2= 2; |
f(x0)= 1, |
f(x1)= 0, |
f(x2)= 1; |
f′(x0)= 0; |
e) x0 = 0, |
x1 = 1, |
x2= 2; |
f(x0)= 1, |
f(x1)= 0, |
f(x2)= 1; |
f′(x2)=0; |
f) x0 = −1, |
x1 = 0, |
x2= 1, |
x3 = 0; |
f(x0)= 0, |
f(x1)= 1, |
f(x2)= 0, |
f(x3)= −1; |
f′(x0)= 0. |
|
|
|
|
|
12. С помощью квадратичных сплайнов построить замкнутую кривую, проходящую через 5 точек:
i |
0 |
1 |
2 |
3 |
4 |
5 |
x |
-2 |
0 |
2 |
1 |
-1 |
-2 |
f |
0 |
1 |
0 |
-1 |
-1 |
0 |
13. Построить кубический интерполяционный сплайн функции, заданной таблично:
i |
0 |
1 |
2 |
3 |
4 |
5 |
x |
0.1 |
0.15 |
0.19 |
0.25 |
0.28 |
0.3 |
f |
1.105 |
1.165 |
1.209 |
1.284 |
1.332 |
1.356 |
С краевыми условиями f′(0.1) = 1, f′(0.3) = 1.2.
Ответы и указания.
1–3. Сравнить результаты вычисления левой и правой частей равенств;
4a). 0.36 10− 4 ; 4b) 0.125 10− 6; 5. Rn = maxf ′′′ 273 h3 ; 6. h = 0.092; 7.
0.2588 ± 0.3 10− 3; 8. 0.80902 ± 0.3 10− 4 ; 9a). 0.6529 ; 9b). 0.6507 ; 9c). 1.4811; 10a). 1.7320 ; 10b). – 0.7321 ; 10c). 0.6180 ; 10d). – 0.7430 ;
11. a) ϕ1 (x) = −(x + 1)2 , |
ϕ2 (x) = 3x2 − 2x −1; |
c) ϕ1 (x) = −2x2 − x + 1, |
ϕ2 (x) = −x + 1 ; |
d)ϕ1 (x) =1 − x2 , ϕ2 (x) = 3x2 − 8x + 5 ;
f)ϕ1 (x) = (x + 1)2 , ϕ2 (x) =1 + 2x − 2x2 , ϕ3 (x) =1 + 6 x − 5x2 ;
12.ϕ1 (x) =1 − x42 , ϕ2 (x) =1 − x42 , ϕ3 (x) = −2x2 +7 x −6,
ϕ4 (x) = 32 x2 − 52 , ϕ5 (x) = −2x2 −7 x −6.
IV. Численное дифференцирование
1. Постановка задачи
Основная идея численного дифференцирования функций – дифференцирование интерполяционного многочлена. Пусть функция f(x)
27

задана в узлах, Ln(x) – интерполяционный многочлен, которые связаны соотношением
(1)
где остаток равен
R(x)= (M+n+)1 ωn (x).
n 1 !
Тогда k-производная вычисляется по формуле:
d k f (x)= d kϕ(x)+ d k R . dxk dxk dxk
Последнее слагаемое в этой формуле представляет собой погрешность формулы численного дифференцирования.
2. Простейшие формулы численного дифференцирования
В качестве интерполирующей функции выберем интерполяционный многочлен в форме Ньютона:
f (x)≈ Ln (x)= f (x0 )+ (x − x0 ) f (x0 , x1 )+ (x − x0 )(x − x1 ) f (x0 , x1 , x2 )+...
Вводя обозначение ξi = x − xi , можно записать многочлен в виде |
||||||
|
f ≈ Ln (x)= f0 +ξ0 f (x0 , x1 )+ξ0ξ1 f (x0 , x1 , x2 )+ξ0ξ1ξ2 f (x0 , x1 , x2 , x3 )+... |
|||||
Тогда последовательное дифференцирование дает |
|
|||||
|
|
df |
= Ln′ (x)= f (x0 , x1 )+ (ξ0 +ξ1 )f (x0 , x1 , x2 )+ |
(2) |
||
|
|
|
||||
|
|
dx |
|
+ (ξ0ξ1 +ξ0ξ2 +ξ1ξ2 )f (x0 , x1 , x2 , x3 )+.... |
||
|
|
|
|
|
|
|
|
d 2 f |
|
= Ln′′(x)= 2 f (x0 , x1 , x2 )+ 2(ξ0 +ξ1 +ξ2 )f (x0 , x1 , x2 , x3 )+... |
(3) |
||
|
dx2 |
|||||
|
|
|
|
|||
|
|
d 3 f |
|
= Ln′′′(x)=6 f (x0 , x1 , x2 , x3 )+... |
(4) |
|
|
|
dx3 |
|
|||
|
|
|
|
|
||
Ограничиваясь некоторым количеством слагаемых в выражениях
(2)- (4) получают формулы численного дифференцирования.
Одночленные формулы численного дифференцирования. Если в правой части (2) − (4) удержать только первые слагаемые, то получим следующие выражения для производных:
|
′ |
|
|
f1 |
− f0 |
|
, |
|
|
|
|
(5) |
||
|
f (x) ≈ |
|
|
|
|
|
|
|
|
|
||||
|
|
x1 |
− x0 |
|
|
|
|
|
||||||
′′ |
|
2 |
|
|
|
f2 − |
f1 |
|
|
f1 − |
f0 |
|
|
|
|
|
|
|
|
|
− |
|
|
. |
(6) |
||||
f (x) ≈ |
x2 |
|
|
|
|
|
|
|
|
|||||
|
− x0 x2 − x1 |
|
x1 − x0 |
|
||||||||||
28
Здесь использованы выражения для разделенных разностей. Подобные формулы, в которых в качестве главного члена используется первое слагаемое в (2) – (4), называются одночленными форму-
лами. На равномерной сетке |
xi+1 |
− xi = h = const |
соотношения (5)- |
|||||
(6) имеют вид: |
|
|
f1 − |
f0 |
|
|
|
|
′ |
|
|
, |
|
(5a) |
|||
f (x) = |
|
|
|
|
||||
h |
|
|
|
|||||
′′ |
= |
f2 |
− 2 f1 |
+ f0 |
. |
(6a) |
||
|
|
|
||||||
f (x) |
|
h2 |
|
|
||||
|
|
|
|
|
|
|
||
В формулах (5) - (6) значение производной следует относить к одному из узлов, по которым проводится интерполяция. Особенностью одночленных формул является то, что они дают одинаковое выражение производной во всех узлах. Например, в формуле (5a) f0′ = f1′, а в формуле (6a) f0′′= f1′′= f2′′. Однако погрешности фор-
мул в разных узлах могут отличаться.
Двучленные формулы численного дифференцирования. Различные формулы для вычисления производной получаются в узлах интерполяции, если в (2) − (3) учесть первые два слагаемых. Двучленные формулы первой производной на равномерной сетке имеют следующий вид:
f ′(x0 ) = f |
0′ = |
−3 f0 +4 f1 − f2 |
|
||||
|
|
2h |
|
|
|||
|
|
|
|
|
|
||
f ′(x1 )= f1′ = |
f 2 − f0 |
|
|
|
|||
2h |
|
|
|||||
|
|
|
|
|
|
||
′ |
′ |
|
|
f0 − 4 f1 |
+ 3 f2 |
. |
|
f (x2 ) = f2 = |
|
|
|
|
|||
|
2h |
|
|||||
|
|
|
|
|
|
||
Аналогично можно получить выражения и для второй производной.
3. Вычисление погрешности с помощью представления функции в виде ряда Тейлора. Порядок точности приближенной формулы
Погрешность формулы численного дифференцирования можно вычислить на основе выражения для интерполяционного многочлена (1). Этот метод вычисления погрешности не единственный, удобнее точность вычислений оценивать с помощью ряда Тейлора (в общем случае формулы Тейлора) представления исходной функции в виде степенной функции. Если функция f(x) обладает всеми непрерывными производными в окрестности точки x = a , то она может быть представлена в виде бесконечного ряда
29

f (x) = |
f (a) + |
(x − a) |
′ |
(x − a)2 |
′′ |
∞ |
(x − a)n |
f |
(n) |
(a) (7) |
|
|
|
|
|||||||
1! |
f (a) + |
2! |
f (a) +…= ∑ |
n! |
|
|||||
|
|
|
|
n=0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Если функция в окрестности точки x = a имеет непрерывные производные лишь до n–го порядка включительно, то она может быть представлена в виде конечной суммы (формула Тейлора):
f (x) = f (a) + |
(x − a) |
′ |
(x − a)2 |
f |
′′ |
|
|
|
|
||
1! |
|
2! |
|
|
|
|
|||||
|
f (a) + |
(a) +…+ |
|
|
|||||||
|
+ |
(x −a)n−1 |
|
f (n−1) (a) |
+ |
(x −a)n |
|
f (n) (ξ) , |
(8) |
||
|
|
|
n! |
||||||||
|
|
|
(n −1)! |
|
|
|
|
|
|
||
где точка ξ принадлежит промежутку (a, x). На равномерной сетке для промежутка (x, x+h) выражения (7) и (8) можно записать в следующем виде:
|
|
|
|
|
|
|
h |
|
|
|
|
h |
2 |
|
|
|
|
|
∞ |
n |
|
|
|
|
|
|
|||||
f (x + h) = f (x) + |
|
f ′(x) + |
|
|
f ′′(x) +…= ∑ |
h |
|
|
f (n) (x) |
|
|
(7a) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
1! |
|
2! |
|
|
|
|
|
n=0 n! |
|
|
|
|
|
|
||||||||||
f (x |
+ |
h) |
= |
f (x) |
+ |
h |
|
|
f |
′ |
+ |
h 2 |
f |
′′ |
+ |
… |
+ |
hn−1 |
|
|
f |
(n−1) |
(x) |
+ |
Rn (x) |
, (8a) |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
1! |
(x) |
2! |
(x) |
|
|
(n −1)! |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Rn (x) = |
f (n) (ξ) |
, |
ξ(x, x+h) . |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 1. Погрешность одночленных формул дифференцирования.
Во всех простейших одночленных формулах, полученных из интерполяционной формулы, имеется одна особенность: по определению, левая часть равенства содержит зависимость от аргумента, в то время как главное слагаемое правой части от координаты не зависит. В подобных формулах вся зависимость от аргумента содержится в погрешности. При оценке точности формул численного дифференцирования используем свойство локальности погрешности интерполяционного многочлена, т.е. зависимости погрешности от координаты.
Рассмотрим формулу первой производной (5a) и оценим ее погрешность в узлах x0 и x1. Для этого используем следующий прием: предположим, что функция бесконечно дифференцируема, произведем разложение правой части (5a) в ряд Тейлора в соответствующем узле, и сравним результат с левой частью. В окрестности точки x0 имеем:
f1 = f (x0 + h)= f0 + hf0′ + h22 f0′′ +...
30
