
Курс лекций Оптическая физика
.pdf
301
Здесь ( ) – линейная диэлектрическая восприимчивость. Если подставить в (25.12) полученное согласно (25.11) выражение для q1, то
( ) |
|
Ne2 |
|
|
|
(25.13) |
|
m[( 02 |
|
||
|
2 ) i ] |
||
Это известная из классики формула для диэлектрической восприимчивости. Теперь найдем желаемую амплитуду второй гармоники q2 на частоте 2ω. Приравнивая коэффициенты при
e2i t |
в (25.10), получим с учетом (25.11): |
|
|
q2 |
De2[E( ) ]2 |
(25.14) |
|
2m2[( 02 2) i ]2[ 02 4 2 2i ] |
|||
Аналогично (25.12), запишем выражение для нелинейной поляризации на частоте 2ω:
P(2 ) (t) Ne(q2e2i t к.с.) 1{d(2 )[E( ) ]2 e2i t к.с.}(25.15) 2 2
Обозначим комплексную амплитуду поляризации Р(2ω) . Тогда Р(2ω) = =d(2 )E( )E( ) . Таким образом, d(2ω) – это отношение комплексной амплитуды поляризации к квадрату амплитуды поля на основной частоте. Согласно (25.14), имеем для d(2ω):
d |
(2 ) |
|
|
|
|
|
DNe3 |
|
(25.16) |
|
|
|
|
2 |
[( 02 2) i ]2( 02 2 |
|
|||||
|
|
|
2m |
2i ) |
||||||
|
|
Перепишем (25.16), введя нелинейную восприимчи- |
||||||||
вость Χ(2ω): |
|
|
|
|
|
|
||||
|
|
|
d |
(2 ) |
|
mD[ ( )]2 (2 ) |
|
(25.17) |
||
|
|
|
|
|
2N2e3 |
|||||
|
|
|
|
|
|
|
|
|
||
Выражение (25.17) получено в предположении об изотропности среды. В действительности все кристаллы обладают анизотропией, т.е. связь между полем и поляризацией среды следует записывать не в виде P(2 ) d(2 )E( )E( ) , а в виде
умножения вектора E(Ex ,Ey ,Ez ) на тензор d(2ijk ) , где каждая
компонента вектора P(2 ) запишется в виде:
302
Pi(2 ) |
dijk(2 )E(j )Ek( ) |
(25.18) |
|
j,k x,y,z |
|
Кристаллы, в зависимости от того, остается ли кристаллическая структура неизменной при инверсии, т.е. замене вектора r(x,y,z) на ( r) ( x, y, z), подразделяются на две группы: инверсионно-симметричные и не обладающие таким свойством. В кристаллах, обладающих инверсионной симметри-
ей, все нелинейные оптические коэффициенты dijk(2 ) должны быть равны нулю. Это следует из соотношения (25.18), если
Е( ) E( )
представить себе, что при изменении знаков у j и k изме-
нившееся электрическое поле «видит» кристалл, идентичный первоначальному, т.е.
Pi(2 ) dijk(2 ) ( E(j ) )( E(k ) ) |
(25.19) |
j,k |
|
Соотношения (25.18) и (25.19) могут одновременно вы-
полняться только при dijk 0. Это означает, что в кристаллах,
обладающих инверсной симметрией, генерация второй гармоники невозможна.
Тензорная запись соотношения между полем и поляризацией безусловно необходима при конкретных расчетах и конструировании нелинейных умножителей оптической частоты. При этом приходится сталкиваться с довольно громоздкими вычислениями. Однако для оценок, позволяющих выяснить условия максимального коэффициента преобразования энергии из основной гармоники во вторую, тензорная запись не обязательна. Поэтому в дальнейшем ограничимся скалярной формой записи.
Разделим поляризацию на линейную (пропорциональ-
ную Е( ) (r,t)) и нелинейную части:
P(r,t) 0E(r,t) PNL(r,t)
Полагая, что векторы PNL(r,t) и E(r,t) параллельны,
перейдем к скалярной форме записи волнового уравнения:
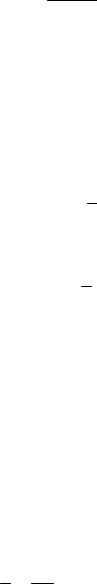
2E(r,t) E(r,t)
t
|
|
|
|
303 |
|
2E(r,t) |
|
2 |
|
|
|
|
|
PNL(r,t)(25.20) |
t2 |
t2 |
Нетрудно видеть, что уравнение (25.20) выступает здесь как замена уравнения колебаний электрона (25.8), поскольку есть необходимость проследить за распространением волн с соответствующими частотами в конфигурационном пространстве кристалла, чего, разумеется, нельзя сделать, если рассматривать только колебания электрона вблизи выбранного положения рав-
новесия. Представим поле E(r,t) как суперпозицию трех плоских волн с различными частотами ω1, ω2 и ω3 , распространяющихся в направлении z:
E( 1) (z,t) 1[E1(z)ei( 1t k1z) к.с.] 2
E |
( |
) |
(z,t) |
1 |
[E2 |
(z)e |
i( |
t k |
z) |
к.с.] |
(25.21) |
2 |
|
|
2 |
2 |
|
||||||
|
2 |
|
E( 3 ) (z,t) 1[E3 (z)ei( 3t k3z) к.с.] 2
Мгновенное значение суммарного поля:
E(z,t) E1( 1) (z,t) E2( 2 ) (z,t) E3 |
( 3) (z,t) (14.22) |
Заметим, что представление (25.21)-(25.22) является более общим, чем это требуется для описания генерации второй гармоники, поскольку учитывает произвольные значения частот. Это значит, что аналогичным образом можно рассматривать и генерацию более высоких гармоник, а также нелинейные параметрические явления и резонансные нелинейные эффекты в изотропных средах.
Подставим (25.22) в волновое уравнение (25.20) с учетом (25.21). Тогда оно распадется на 3 уравнения, каждое из которых содержит только члены, описывающие колебания на одной из трех частот. Члены, содержащие PNL (r,t), в соответствии с предположением об изотропности среды, имеют вид:
2
1 d 2 E1E2ei[( 1 2 )t (k1 k2 )z]
2 t
|
|
|
|
|
|
|
|
|
|
304 |
или |
|
|
|
|
|
|
|
|
||
1 |
|
2 |
|
i[( |
)t (k |
k |
)z] |
|
||
|
|
d |
|
E3E |
2e |
3 2 |
3 |
2 |
|
, |
2 |
t2 |
|
||||||||
т.е. |
содержат |
комбинационные частоты 1 2 и |
||||||||
3 2 . |
В случае несинхронности (произвольного соотноше- |
|||||||||
ния частот) они не могут, вообще говоря, влиять на колебания
на |
отдельно |
взятой частоте |
ω1, ω2 или ω3. |
Но в случае |
||||||
|
|
|
член d |
2 |
E |
E |
ei[( 1 2 )t (k1 k2 )z] |
может рас- |
||
|
t2 |
|||||||||
1 |
|
2 |
3 |
|
1 |
|
2 |
|
|
|
сматриваться как источник волны на частоте 3. Физиче-
ский смысл такого взаимодействия (появляющегося только при наличии члена PNL) означает преобразование потоков энергии на частотах 1 и 2 в поток энергии на частоте 3 и наоборот. В
случае 1 2 3 волновое уравнение (25.20)для волны с частотой ω1 запишется в виде:
|
2 |
E |
( ) |
(z,t) 1 |
E( 1 ) |
|
2E( 1 ) |
|
|||||||
|
1 |
|
|
|
|||||||||||
|
|
t |
t2 |
||||||||||||
|
|
|
2 |
|
|
E |
3 |
(z)E |
(z) |
|
i[( 3 2 )t (k3 k2 )z] |
(25.23) |
|||
d |
|
|
[ |
|
2 |
|
|
e |
|||||||
t2 |
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||
к.с.]
Преобразуем (25.23) к более простому виду, предпола-
гая, что распространение волны E( 1) (z,t) вдоль оси z характеризуется медленным по сравнением с основной частотой изме-
нением амплитуды: |
k1 |
dE1(z) |
|
d2E1(z) |
, а также заменяя вез- |
dz |
dz2 |
||||
|
|
|
|
|
|
де дифференцирование по времени умножением на соответ-
ствующий частотный множитель: |
|
i |
. Учтем также, |
|
|
||||
|
|
t |
1,2,3 |
|
что |
|
|
|
|
|
|
|
|
|
k2 |
2 . Получим: |
|
|
|
1 |
1 |
|
|
|

305
dE1 |
|
1 |
|
|
E |
|
|
i 1 |
|
|
dE |
E e i(k3 k2 k1)z |
dz |
|
|
|
|
|
|||||||
2 |
|
|
1 |
2 |
|
3 |
2 |
|||||
(25.24)
Аналогичным образом получим уравнения для распространения волн с частотами ω2 и ω3 :
dE2 |
|
|
2 |
|
|
|
|
|
|
|
|
i 2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
E2 |
|
|
|
|
dE1E3e i(k1 k3 k2)z |
|||||||||||||||
dz |
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
dE3 |
|
|
3 |
|
|
|
|
|
|
|
i 3 |
|
|
|
|
|
dE |
|
|
|
||||
|
|
|
|
|
E |
|
|
|
|
E |
|
e i(k1 k2 k3)z |
||||||||||||
dz |
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
3 |
2 |
|
|
|
|
1 |
|
2 |
|
|||||||||||
(25.25)
Уравнения (25.24)-(25.25) имеют достаточно общий смысл и описывают нелинейные параметрические взаимодействия. Их легко обобщить и на анизотропный случай, вводя различные для разных волн значения диэлектрических постоянных ε1, ε2, ε3 и вспоминая о тензорном характере нелинейных восприимчивостей dijk.. Соответствующие расчеты проводились для многих кристаллов и их результаты представлены в справочной литературе. Для простейшего случая генерации второй гармоники примем, что 1 2 . Тогда уравнения для Ε1 и Ε2
оказываются комплексно сопряженными, и достаточно рассматривать только Ε1 и Ε3 , имея в виду, что ω3 = 2ω. Пренебрегая поглощением (σ1,2,3 = 0), запишем (25.24)-(25.25) в виде:
dE(2 ) |
|
|
|
|
( ) |
2 |
i( k)z |
|
|
|
i |
|
d[E |
|
(z)] e |
|
(25.26) |
||
|
|
|
|
||||||
dz |
|
|
|
|
|
|
|||
где введено обозначение k k(2 ) 2k( ) . Допустим, что ослабление входной волны Е(ω) из-за преобразования ее в
волну Е(2ω) незначительно. Пренебрежем поэтому зависимостью Е(2ω) от z , а на входе волны с частотой 2ω еще нет (Е(2ω) =0 ). То-
гда интегрирование (25.26) в пределах оптической длины кристалла l дает:
|
(2 ) |
|
|
|
|
|
( ) |
2 ei kl 1 |
||
E |
|
(l) i |
|
d[E |
|
] |
|
|
||
|
|
|
i k |
|||||||
|
|
|
|
|
|
|
|
|||
306
Отсюда найдем выходную интенсивность второй гармо-
ники:
|
|
|
|
|
|
|
2d2 |
|
|
|
|
sin |
2 |
( |
k l |
) |
|||||
|
(2 ) |
|
(2 ) |
|
|
(2 ) |
4 |
|
2 |
|
2 |
|
|||||||||
E |
|
(l)E |
|
(l) ( |
|
|
) |
|
[E |
|
] |
l |
|
|
|
|
|
|
|||
|
|
|
0 |
n2 |
|
|
( |
k l |
) |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(25.27)
В (25.27) введен показатель преломления: n2 .
0
Пользуясь (25.27), можем найти светимость излучения второй гармоники (если ввести сечение выходного пучка А):
|
P(2 ) |
|
|
|
|
|
|
|
|
1 |
|
(2 ) |
2 |
||||
I |
|
|
|
|
|
E |
|
(25.28) |
|
|
|
|
|
||||
A2 
иэффективность преобразования во вторую гармонику:
P(2 )
P( )
|
|
|
32 |
2d2l2 |
|
sin2 |
k l |
|
|
P( ) |
|||||
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
(25.29) |
||||||
2 |
0 |
|
|
n |
|
|
|
|
|||||||
|
|
|
|
|
k l |
|
|
A |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда следует, что эффективность преобразования во вторую гармонику определяется продольным размером кристалла, интенсивностью входного пучка и, что особенно интересно, величиной Δk. Зависимость от Δk имеет интерференционный характер. Максимальная эффективность преобразования достигается при Δk = 0. Если Δk ≠ 0 , то имеет место интерференция волны второй гармоники самой с собой, т.е. энергия перекачивается от исходной волны во вторую гармонику и обратно. Два соседних максимума этой интерференционной картины
удалены на расстояние l |
k |
|
2 |
|
2 |
, определяющее |
|
k(2 ) 2k( ) |
|||||
|
|
k |
|
|||
максимальную длину кристалла, при которой можно наблюдать
излучение второй гармоники. Имея в виду, что k n , можно c
записать Δk в виде
307
k 2 |
|
[n2 n ] |
(25.30) |
|
|||
|
c |
|
|
откуда для длины когерентности lk имеем:
lk (25.31)
2[n2 n ]
Здесь λ – длина волны основного пучка в свободном пространстве. Если использовать произвольный кристалл, то, как правило, показатель преломления возрастает с частотой, и
добиться выполнения условия n2 n невозможно. Поэтому в первых экспериментах по наблюдению второй гармоники излучения рубинового лазера использовались тонкие ( 100 мкм) слои кристалла и очень большие интенсивности входного излучения. Коэффициент в этих экспериментах (1961 г.) составлял
10-11…10-12. Между тем условие n2 n выполнить вполне возможно, если воспользоваться двулучепреломляющим кристаллом, у которого волны с частотами и 2 — разного типа (одна — обыкновенная, другая — необыкновенная). В качестве примера можно взять одноосный отрицательный кристалл. Зависимость показателя преломления необыкновенной волны от угла между направлением распространения и оптической осью имеет вид
1 |
|
cos2 |
|
sin2 |
|
||
|
|
|
|
|
(25.31) |
||
ne2 |
|
n02 |
ne2 |
|
|||
( ) |
|
|
|
||||
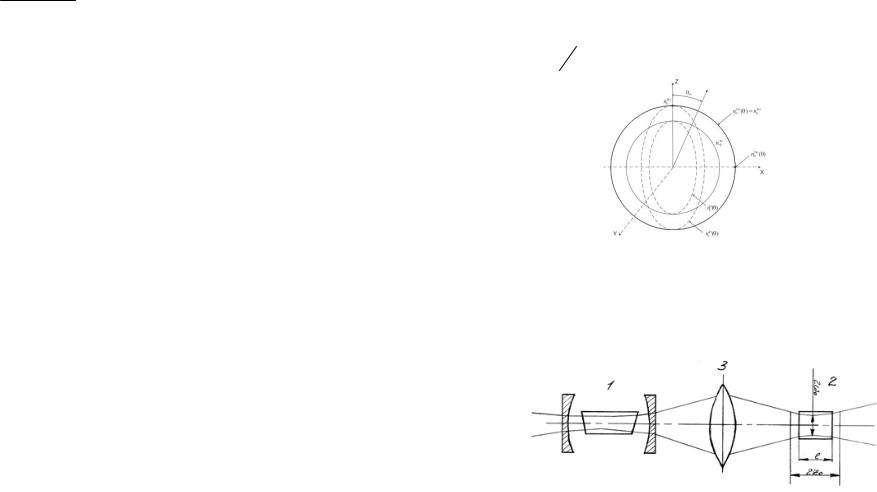
Если ne2ω < noω , то существует угол θm , при котором ne2 ( m ) n0 . Таким образом, если основной пучок на частоте
ω — это обыкновенная волна, распространяющаяся вдоль направления θm, то пучок второй гармоники будет распространяться вдоль того же направления θm как необыкновенная волна
(рис. 25.2).
Из (25.31) можно получить значение θm для данного одноосного отрицательного кристалла:
|
|
(n |
|
2 |
n |
2 |
2 |
|
sin2 m |
|
0 ) |
|
0 |
|
(25.32) |
||
|
|
2 |
|
|
2 |
|||
|
|
ne2 |
n02 |
|
||||
308
Очевидно, что выполнение условия n2 n очень критично к поляризации падающего излучения. Основной пучок в кристалле должен обладать поляризацией обыкновенной волны. Кроме того, можно указать другие причины малого коэффициента преобразования во 2-ю гармонику в экспериментах 1961 г.: работа в приближении плоской волны заставляет добиваться очень больших превышений над порогом генерации («тянуть»
отношение |
Р |
до безумно больших величин). |
|
А |
|
Рис. 25.2. Нормальные поверхности показателей преломления для обыкновенного и необыкновенного лучей в одноосном отрицательном (ne<no) кристалле. Направление оптической оси совпадает с осью Z. Если ne( )<no( ), то условие ne( )( )<no( )
может быть выполнено для некоторого значения m. Значительно целесообразнее работать с фокусировкой
входного пучка. (рис. 25.3)
Рис.25.3. Схема генерации второй гармоники при расположении нелинейного кристалла вне резонатора с фокусировкой гауссова пучка: 1 — лазер, 2 — нелинейный кристалл, 3 — линза.
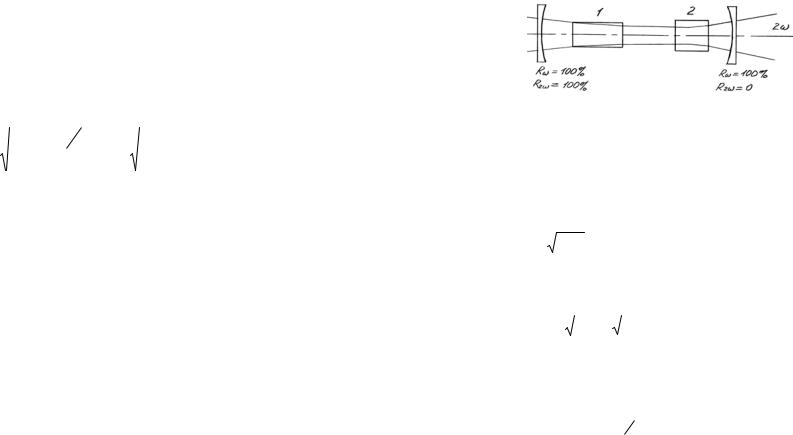
309
В самом деле, допустим, что лазер, работающий на основной гармонике, излучает гауссов пучок с конфокальным па-
раметром z0 |
w2n |
||
0 |
(n – показатель преломления активной |
||
|
|||
|
|
||
среды в резонаторе). Если z0 l(l – оптическая длина преобра-
зующего кристалла), то внутри кристалла поперечное сечение пучка можно считать постоянным.
Напомним, что физический смысл параметра zo есть расстояние от перетяжки пучка до плоскости, где сечение пучка в 2 раза больше, чем в перетяжке. Считая, что z » l, запишем:
|
|
|
|
|
|
|
r2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
2 w |
|||||
P( ) |
|
|
|
E0e |
w02 |
|
dr |
E |
0 |
0 |
|||||||
|
|
|
|
|
4 |
|
|||||||||||
2 |
|
0 |
|
|
|
|
|
|
|
|
|||||||
Тогда вместо (25.29) для эффективности преобразования можно записать:
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
sin |
2 k l |
|
|
|||||
|
|
|
2 |
2 |
d |
2 |
l |
2 |
|
P |
( ) |
|
|
|
|
|
||||||
2 |
|
|
||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
(25.33) |
|||||||||
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|||||||||
|
0 |
|
|
n |
|
|
|
w |
|
k l |
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь n3 n 2 n2 .
Согласно (25.33), выходная мощность во 2-й гармонике может быть увеличена за счет уменьшения перетяжки wо. Это возможно до тех пор, пока zо не станет сравнимой с l. В случае,
когда w2 |
|
l |
(конфокальная фокусировка), дальнейшее уве- |
|
|||
0 |
|
2 n |
|
личение η уже невозможно. Поэтому довольно быстро стал применяться более радикальный способ увеличения η – помещение нелинейного кристалла внутрь резонатора. В самом де-
ле, внутри резонатора плотность мощности в 1 R 1 раз больше, чем снаружи. При R ~ 1 эта величина может быть сделана очень большой.
Рассмотрим для примера резонатор, в котором при данной скорости накачки максимальная выходная мощность достигается при оптимальном пропускании зеркала (полагая, что пре-
310
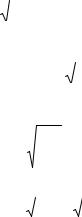
вышение не очень велико, что реализуемо в случае лазера на Nd:YAG). Заменим выходное зеркало глухим (100% отражения) по отношению к излучению частоты ω, а в резонатор поместим нелинейный кристалл (рисунок 25.4).
Рис. 25.4. Схема внутрирезонаторного преобразования основной частоты лазера на Nd:YAG с помощью нелинейного кристалла BaNaNb5O15 с практически полным подавлением основной гармоники в выходном излучении: 1 — активный элемент лазера; 2 — нелинейный.
Величина оптимального пропускания при небольших превышениях дается формулой
Tопт |
G0 |
(25.34) |
где Go – ненасыщенный однопроходный показатель усиления, β – распределенные однопроходные потери. Выходная мощность в этом случае равна
P0 IsA |
|
|
|
2 |
(25.35) |
G0 |
|
где Ιs - интенсивность насыщения В силу предположения о полном преобразовании выходной энергии во 2-ю гармонику будем считать, что потери на зеркале полностью совпадают с коэффициентом преобразования:
|
|
|
|
|
|
|
|
|
|
|
|
k l |
||||||
~ |
|
P(2 ) |
|
|
|
32 |
2d2l2 |
sin2 |
|
|
|
P( ) |
||||||
|
2 |
|||||||||||||||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
3 |
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
k l |
|
|
|||||||||
|
|
P |
|
|
0 |
|
|
n |
|
( |
)2 |
|
A |
|||||
|
|
|
|
|
2 |
|||||||||||||
(25.36) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ω) |
|
|||
Обозначим в (25.36) множитель при Р |
как k : |
|||||||||||||||||
~ |
~ |
( ) |
|
|
|
|
|
|
|
|
|
(25.37) |
|
|||||
T kP |
|
|
|
|
|
|
|
|
|
|
||||||||
311
Подставляя (25.37) в (25.34), видим, что оптимальное преобразование во вторую гармонику имеет место, если
~ |
( ) |
опт |
|
|
|
|
|
|
G0 |
(25.38) |
|||||
kP |
|
||||||
Суммарные однопроходные потери для основного излу-
чения:
|
~ |
( ) |
опт |
|
|
|
опт |
|
G0 |
||||
kP |
|
Заменяя в (25.35) выражение для β его оптимальным значением, получим:
(P( ) ) |
|
|
|
|
|
G0 |
|
|
|
||
опт |
I |
A |
|
|
1 |
(25.39) |
|||||
|
|
|
|||||||||
|
s |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Соответственно для второй гармоники: |
|
||||||||||
(P(2 ) )опт |
IsA |
|
|
|
|
2 |
(25.40) |
||||
G0 |
|
||||||||||
Из (25.37) и (25.40) можно выразить постоянную нели-
~
нейной связи k в оптимальном случае:
~ |
|
~ |
( ) |
опт |
|
|
|
|
|
kP |
|
|
(25.41) |
||||
kопт |
|
|
|
|
|
|
||
P( ) |
|
I |
A |
|||||
|
|
|
опт |
|
s |
|
|
|
~
Заметим, что kопт не зависит от накачки (в (25.41) не
~
входит ненасыщенный показатель усиления Go). Поскольку k зависит не только от l, d и А , но и от фазового рассогласования Δk·l (т.е. от направления распространения волны относительно
~
оптической оси кристалла), можно менять k , изменяя ориентацию кристалла в резонаторе. Условие Δk = 0 называется условием фазового синхронизма. Его выполнение является основной задачей при юстировке лазера с нелинейным преобразованием частоты.
312
Лекция 26
Эффекты самовоздействия, параметрические эффекты и вынужденное рассеяние Самофокусировка луча
Оптическое гетеродинирование и параметрическое усиление света Вынужденное рассеяние Обращение волнового фронта Динамическая голография или четырехволновое взаимодействие Вынужденное комбинационное рассеяние Лазерное охлаждение
Наряду с появлением «лишних» частот в спектре сигнала, проходящего через нелинейную среду, имеют место и эффекты «самовоздействия» излучения, выражающиеся в том, что оптические свойства среды изменяются по отношению к распространению самого интенсивного сигнала. Для объяснения «самовоздействия» достаточно представления поляризации в скалярном приближении:
P |
( E EE E2E ...) |
(26.1) |
|
0 |
2 |
3 |
|
Вклад в поляризуемость среды на частоте ω дают первый и третий члены (линейная и кубичная восприимчивость). Наличие члена с 3 эквивалентно появлению в ε(ω) и n(ω) сла-
гаемого, пропорционального E20 , т.е.
n( ) n0 n2E02 |
(26.2) |
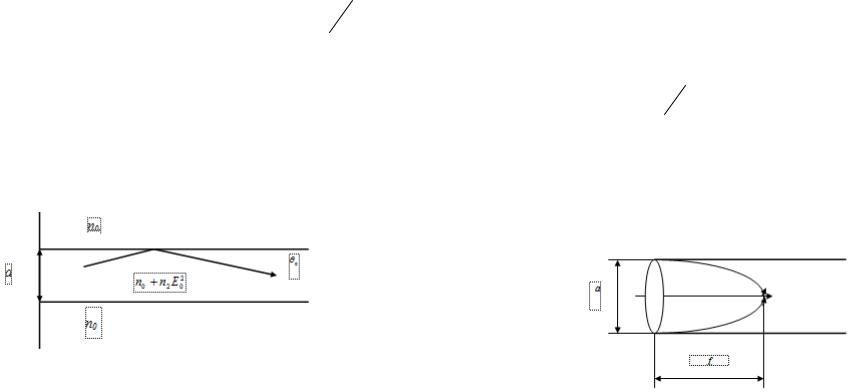
Иначе говоря, ограниченный интенсивный пучок света делает среду оптически неоднородной. Но в таком случае на продольной «виртуальной» (Е0 = 0) границе пучка возможно полное внутреннее отражение – в том случае, если n2 0. Если, аналогично волоконной оптике, ввести «угол скольжения» 0 ,
то условие полного отражения на виртуальной границе можно записать как
(n0 n2E02 )cos 0 |
n0 |
(26.2) |
|
|
|
|
|
|
|
|
313 |
|
(рис. 26.1). В параксиальном приближении cos 0 |
1 |
2 |
|
, |
|||||
0 |
2 |
||||||||
|
|
|
n2 |
|
|
|
|
|
|
поэтому |
2 |
2 |
E2 |
(26.3). |
|
|
|
|
|
|
n0 |
|
|
|
|
||||
|
0 |
|
0 |
|
|
|
|
|
|
С другой стороны, факт ограниченности пучка по диаметру можно трактовать как наличие диафрагмы, вызывающей дифракцию Френеля. Пучок при этом расходится, и предельный угол отклонения от оптической оси можно оценить как
|
|
|
|
|
диф |
|
(26.4) |
||
|
||||
|
|
a |
||
где а – диаметр пучка.
Рис. 26.1. К оценке порога самофокусировки.
Самофокусировка вызывает сжатие пучка, а дифракция — расширение. Следовательно, наблюдать самофокусировку можно
только при 0 диф , т.е. самофокусировка носит пороговый
характер. Порог самофокусировки оценивается в параксиальном приближении из условия
E0min2 |
20n0 |
(26.5) |
|
2n2 |
|||
|
|
Отсюда по известному значению n2 для нелинейной среды можно оценить минимальную мощность светового пучка, необходимую для наблюдения самофокусировки. При Е0 = Е0min площадь сечения пучка при распространении в среде остается постоянной, т.е. пучок сам себе создает световод, в котором отсутствует дифракционная расходимость. Такой режим
314
естественно назвать самоканализацией пучка. При Е0 > Е0min наблюдается самофокусировка, причем лучи искривляются в сторону оптической оси, и эффект усугубляется. Среда ведет себя как собирающая линза с переменным фокусным расстояни-
ем (рисунок 26.2).
Поскольку f ~ |
a |
, искривление лучей по мере при- |
|
E |
0 |
ближения к оптической оси увеличивается. Следовательно, изменяя входную интенсивность, можно управлять положением фокуса (приближать его к месту входа пучка в среду). Это явление, наблюдавшееся экспериментально при прохождении через среду мощных лазерных импульсов (впервые в 1965 г. Н.М. Пилипецким и А.Р. Рустамовым в сероуглероде в режиме свободной генерации рубинового лазера) было образно названо А.М. Прохоровым «бегущим фокусом».
Рис. 26.2. К объяснению схлопа пучка.
Скорость перемещения фокуса в случае коротких импульсов может быть сделана оценочно очень большой (вплоть до субсветовых скоростей). Однако фактическое движение фокуса наблюдаемо в относительно небольших пределах, поскольку при достижении значений Е0, сопоставимых с внутриатомными (а это не так уж много — порядка 104 … 105 В/см), возникает пробой и разрушение среды в области фокуса. Так что разогнать фокус при очень малых (фемтосекундных) длительностях до сверхсветовых скоростей невозможно. Схлоп пучка, т.е. пробой и разрушение среды произойдет гораздо раньше, чем разгон фокуса до релятивистских скоростей.
Параметрическая генерация. Рассмотренный выше случай генерации 2-й гармоники представляет собой частный
315
случай распространения в нелинейной среде двух волн с частотами 1 и 2 при 1 = 2. Если же 1 2, то, помимо основных и кратных частот, в спектре вынужденных колебаний появляют-
ся суммарная и разностная частоты. Такое взаимодействие можно трактовать как следствие изменения оптических параметров среды под действием сильного поля одной из волн ( 1). В результате возникает модуляция с частотой 1 фазы второй волны ( 2), что эквивалентно появлению боковых компонент 1 - 2 и 1 + 2. Практический интерес процессов генерации суммарных и разностных частот обусловлен тем, что при смешении излучения двух лазеров в нелинейной среде получается когерентное излучение в новом (отличном от 1 и 2 диапазоне спектра). Тем самым можно расширить диапазон доступных источников когерентного излучения, не разрабатывая целиком новых лазеров, т.е. не изыскивая новых генерационных переходов. Такая параметрическая генерация получила широкое распространение, начиная с 1962 г. Впервые такие лазеры были созданы группой Е.М. Швома, одного из основоположников прикладной нелинейной оптики и создателей НИИ «Полюс» — ведущего предприятия в электронной промышленности СССР по лазерной технике.
Оптическое гетеродинирование и параметрическое усиление света. Другое, не менее важное, применение нелинейного преобразования частоты — это повышение чувствительности фотоприемных устройств. При нелинейном взаимо-
действии сильного 1 и слабого 2 сигналов амплитуда сигнала разностной частоты возрастает пропорционально корню из произведения амплитуд каждого из сигналов. Если слабый сигнал 2 находится за пределами чувствительности фотоприемного устройства, то путем увеличения амплитуды сигнала 1 можно уверенно обнаружить 2 за счет нелиней-
ного взаимодействия. Такой метод регистрации слабых сигналов был впервые предложен Форрестером (Forrester A.T.) в 1961
г. и получил название оптического гетеродинирования, по аналогии с радиодиапазоном. Справедливости ради следует отметить, что идея оптического гетеродинирования была высказана значительно раньше (Г.С. Горелик, 1947 г.), однако в то вре-
316
мя экспериментальное осуществление этой идеи не удалось, поскольку интенсивность некогерентных источников оказалась недостаточной. Ситуация коренным образом изменилась с появлением лазеров — Форрестер еще с 40-х годов очень внимательно отнесся к идеям Горелика и немедленно по появлении неон-гелиевых лазеров осуществил эксперимент по наблюдению межмодовых биений с выделением разностной частоты сильной и слабой мод. В нашей стране развитие методики оптического гетеродинирования связано прежде всего с именами В.С. Летохова и В.П. Чеботаева, под руководством которых было создано целое новое направление в науке — нелинейная лазерная спектроскопия, а также Л.Н. Курбатова и В.Е. Зуева, под руководством которых были проведены пионерские исследования в части применения оптического гетеродинирования для целей локации и связи.
Наряду с регистрацией слабых сигналов параметрику можно использовать и для непосредственного усиления слабой волны 1 или 2 за счет перекачки энергии из сильной волны 3
. Впервые такой метод параметрического усиления света был предложен С.А. Ахмановым и Р.В. Хохловым в 1962 г. Взаимодействие сильной волны с частотой 3 и слабой (сигнальной) волны с частотой 1 за счет квадратичной восприимчивости 2 приведет к появлению в нелинейной поляризуемости осцилляций на разностной частоте 2 = 3 - 1 . При выполнении век-
торного условия пространственного синхронизма k2 k3 k1
вторичные волны с частотой 2, испускаемые в направлении k2 , складываются синфазно. В результате возникает резонансная перекачка энергии. На квантовом языке параметрическое
усиление можно рассматривать как вынужденный распад фотона ħ 3 на фотоны ħ 1 и ħ 2. Соотношение 3 = 1 + 2 в таком процессе выражает закон сохранения энергии,
k3 k1 k2 - сохранения импульса.
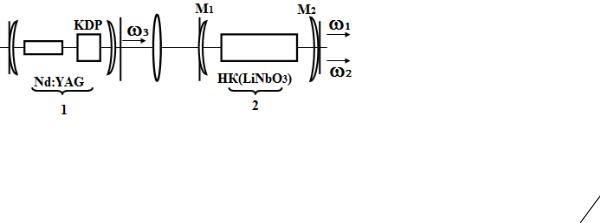
Одна из возможных схем параметрического генератора показана на рисунке 26.3.
317
Рис. 26.3. Схема параметрического генератора:
1 - лазер накачки с удвоителем частоты; 2 – нелинейный кристалл в оптическом резонаторе.
Нелинейный кристалл LiNbO3 (2) расположен в резонаторе как активный элемент. Для волн, распространяющихся в направлении оптической оси, выполняется условие простран-
ственного синхронизма k1o ko2 k3e . Зеркала М1 и М2 имеют
высокие коэффициенты отражения для частот 1 и 2. Зеркало М1 прозрачно для частоты 3 излучения накачки (1). При достаточно большой мощности излучения накачки параметрическое усиление одной из волн 1 или 2 на длине нелинейного кристалла превышает однопроходные потери, выполняя тем самым условие самовозбуждения. Поскольку в направлении, перпендикулярном плоскости зеркал, выполняется условие фазового синхронизма, при небольшом изменении ориентации зеркал относительно оптической оси или других управляющих воздействиях (наложении внешнего электрического или магнитного поля, изменении температуры и т.п.) частоты 1 и 2 изменяются. Полоса перестройки определяется тем диапазоном, для которого в данном нелинейном кристалле выполняется условие пространственного синхронизма. Этот диапазон плавной перестройки обычно гораздо больше традиционного диапазона перестройки частоты генерации в пределах одной линии рабочего перехода при изменении длины резонатора, поскольку частота 3 при этом остается постоянной. Заметим при этом, что выполнение условия пространственного синхронизма для кристалла НК накладывает жесткие требования к источнику накачки в части высокой монохроматичности и малой пространственной расходимости. Смягчение этих требований вызывает резкое возрастание пороговой мощности накачки и снижение КПД.
318
Разработанные на основе высококачественных нелинейных кристаллов LiNbO3 (ниобат лития), Ba2NaNb5O15 («банан»), KDP (дигидрофосфат калия), ADP (дигидрофосфат аммония) параметрические генераторы света позволяют получать когерентное излучение с плавной перестройкой частоты при задающем лазере на второй гармонике Nd:YAG во всем видимом и значительной части ИК диапазона спектра.
Вынужденное рассеяние. Еще один класс нелинейных явлений — это процессы вынужденного рассеяния. Пусть в среде распространяется упругая плоская монохроматическая волна с частотой Ω и волновым вектором q. Ее фазовая ско-
рость q - это скорость звука v , определяемая упругими ха-
рактеристиками среды (модулем Юнга) и средней плотностью ρ. Периодические изменения плотности acos(qr t) приводят к пространственной модуляции показателя преломления
среды δn ~ δρ , т.е. создают фазовую дифракционную решетку.
При падении монохроматического света E0ei(kr t) на такую
решетку появляется дифрагированная волна E1e(k1r 1t) с волно-
вым вектором k1 k q и частотой 1 (если угол
между q и k острый). Если же угол между q и k тупой, то
дифрагированная волна характеризуется вектором k1 k q и
частотой . Если упругие волны обусловлены тепло-
1
вым движением частиц среды (а мы помним, что в конденсированных средах из-за сильной связи между частицами среды тепловое движение можно рассматривать как совокупность всевозможных упругих волн, занимающих диапазон частот от нескольких герц до 1010…1011 Гц), то наблюдаемое на таких волнах рассеяние света называется рассеянием МандельштамаБриллюэна. Указанное рассеяние было предсказано теоретически независимо друг от друга названными учеными и экспериментально открыто также независимо друг от друга в 1928 г. Л.И. Мандельштамом и Г.С. Ландсбергом в СССР и Раманом в Индии. Рассеяние Мандельштама-Бриллюэна можно трактовать
319
как рассеяние фотона исходного пучка света на неоднородностях среды с испусканием или поглощением фонона – кванта
упругих колебаний среды – с импульсом ħk и энергией ħΩ. В элементарном акте рассеяния выполняются законы сохранения энергии и импульса:
ħk ħq=ħ k1; ħω ± ħΩ = ħω1
Если упругие колебания возбуждаются независимо, то рассеяние Мандельштама-Бриллюэна называется спонтанным, или классическим. При этом вероятность испускания фонона и появления рассеянного фотона не зависит от интенсивности падающего излучения. Тем самым классическое МБ-рассеяние является линейным процессом.
Если же упругая волна в кристалле вызывается мощным лазерным излучением, причем она когерентна падающей световой волне, то такое рассеяние называется вынужденным рассе-
янием Мандельштама-Бриллюэна (ВРМБ). ВРМБ было от-
крыто на опыте в 1964 г. Чиао, Таунсом и Стойчевым. Тогда же было установлено, что ВРМБ носит ярко выраженный пороговый характер и наблюдается только при превышении некоторой критической интенсивности падающего света. Процесс ВРМБ можно рассматривать как перекачку энергии от волны ω к волнам Ω и ω-Ω, т.е. как аналог параметрического усиления. Волну Ω в этом случае имеет смысл рассматривать как волну создаваемого светом давления, распространяющуюся в том же направлении и с той же скоростью, что и первичная упругая волна, благодаря которой возникла рассеянная световая волна. При достаточно большой интенсивности исходного пучка света, когда усиление для волн Ω и ω-Ω превысит потери, амплитуды этих волн по мере распространения в среде будут возрастать. Поскольку, в отличие от классического РМБ, возникающее при ВРМБ излучение когерентно, можно обеспечить положительную обратную связь между усиливаемыми световой и упругой волнами.
Обращение волнового фронта (ОВФ). Если падающий первичный пучок пространственно неоднороден, т.е. характери-
320
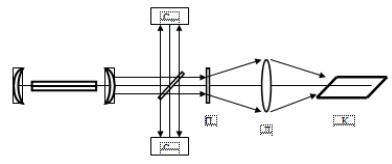
зуется неравномерным распределением интенсивности поперек оптической оси, то при ВРМБ имеет место обращение волнового фронта (ОВФ), не имеющее аналога в классической оптике. Схема эксперимента по наблюдению ОВФ показана на рисунке 26.4.
Рис. 26.4.Схема эксперимента по наблюдению Обращения волнового фронта
Лазерный пучок проходит через делительное зеркало, отражающее небольшую его часть на измерительную систему С1, регистрирующую угловое распределение интенсивности излучения в дальней зоне. Проходящая часть пучка попадает на фазовую пластинку П со случайными неоднородностями. Расходимость пучка при этом возрастает в десятки раз. Затем линза Л с большой апертурой, достаточной для того, чтобы перехватить весь пучок, направляет излучение в кювету К, заполненную сероуглеродом или метаном при высоком давлении. Рассеянный назад свет отражается от делительного зеркала и регистрируется измерительной системой С2, аналогичной системе С1. Сравнение распределений, зарегистрированных системами С1 и С2, показало, что первоначально широкий пучок рассеянного света после прохождения через те же оптические элементы в обратной последовательности становится столь же направленным, как и первоначальный лазерный пучок. Так происходит потому,
что волновой фронт излучения, рассеянного назад в нелинейной среде, в точности воспроизводит сколь угодно сложную структуру волнового фронта падающей волны, отличаясь лишь противоположным направлением распространения (уменьшение
