
- •Выходной сигнал фильтра определяется следующим соотношением
- •1. Цель работы
- •2. Литература
- •3. Подготовка к лабораторной работе
- •4. Контрольные вопросы
- •5. Содержание работы
- •6. Содержание отчета
- •7. Методические указания по выполнению работы
- •Сформируем взвешенную функцию ошибки
- •5.1. Выполните синтез цифрового полосового эллиптического фильтра по программе «Filtrd».
РАБОТА №2
СИНТЕЗ НЕРЕКУРСИВНОГО ЦИФРОВОГО ФИЛЬТРА МЕТОДОМ РЯДА ФУРЬЕ И «ОКНА». ИССЛЕДОВАНИЕ ФИЛЬТРА
1. ЦЕЛЬ РАБОТЫ
Изучение синтеза нерекурсивных цифровых фильтров с линейной ФЧХ методом разложения требуемой АЧХ в ряд Фурье и применения оконных функций для ослабления явления Гиббса.
Расчет АЧХ и ФЧХ фильтра, сравнение реальной АЧХ с требуемой.
Моделирование процесса фильтрации и исследование селективных свойств фильтра.
2.ЛИТЕРАТУРА
1.Приложение к лабораторной работе.
2. В.Г.Иванова, А.И.Тяжев. Цифровая обработка сигналов и сигнальные процессоры, Самара, 2008г.
3. ПОДГОТОВКА К ЛАБОРАТОРНОЙ РАБОТЕ
Изучите указанную в разделе 2 литературу и ответьте на контрольные вопросы.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
Дайте определение цифровому фильтру.
Какой цифровой фильтр называют нерекурсивным?
Дайте определение импульсной характеристике фильтра. Что такое БИХ - и КИХ - фильтры?
Дайте определение системной функции фильтра.
Что понимают под комплексным коэффициентом передачи фильтра?
Как осуществляется переход от системной функции к комплексному коэффициенту передачи фильтра?
Докажите, что частотная характеристика фильтра (зависимость комплексного коэффициента передачи фильтра от частоты) является периодической функцией частоты. Чему равен период этой функции?
Дайте определение АЧХ и ФЧХ фильтра.
Приведите структурную схему нерекурсивного цифрового фильтра – графическое представление алгоритма нерекурсивной цифровой фильтрации. Какое условие нужно выполнить, чтобы обеспечить линейность ФЧХ этого фильтра?
Поясните сущность синтеза нерекурсивного цифрового фильтра методом ряда Фурье.
Что такое явление Гиббса? Как зависит частота пульсаций АЧХ фильтра от длины линии задержки?
Как влияют оконные функции на уровень пульсаций АЧХ и ширину переходной полосы АЧХ фильтра?
5. СОДЕРЖАНИЕ РАБОТЫ
5.1. Выполните синтез цифрового ФНЧ методом ряда Фурье и «окна» при использовании прямоугольного окна и окна Хемминга и пяти значениях длины линии задержки: K=5, 10, 15, 20, 25.
Исходными данными для синтеза фильтра являются:
Частота дискретизации Fd,
Граничная частота полосы пропускания Fg,
Эти данные приведены в таблице 1.
Таблица 1
|
Номер бригады |
Значения параметров | |
|
Fd, МГц |
Fg, МГц | |
|
1 |
10 |
1 |
|
2 |
10 |
2 |
|
3 |
16 |
1 |
|
4 |
16 |
2 |
|
5 |
1 |
0.1 |
|
6 |
1 |
0.2 |
5.2. Рассчитайте АЧХ и ФЧХ фильтра в интервале от нуля до половины частоты дискретизации при прямоугольном окне и окне Хемминга и при минимальной длине линии задержки (K=5).
Определите полосу пропускания фильтра на уровне 0.707 и максимальный уровень пульсаций в полосе задерживания при прямоугольном окне и окне Хемминга.
5.3. Снимите зависимость коэффициента прямоугольности фильтра от длины линии задержки при прямоугольном окне и окне Хемминга.
5.4. Снимите зависимость ослабления в полосе задерживания от длины линии задержки при прямоугольном окне и окне Хемминга.
5.5. Определите импульсную характеристику фильтра, наблюдая выходной сигнал фильтра при действии на входе единичного отсчета при прямоугольном окне и окне Хемминга.
5.6. Выполните моделирование процесса фильтрации при действии на входе фильтра сигнала в виде случайной последовательности прямоугольных импульсов и синусоидальной помехи.
Параметры сигнала и помехи:
Количество отсчетов в элементарной посылке сигнала nv,
Максимальный уровень сигнала X, минимальный уровень сигнала –X,
Амплитуда помехи Xp,
Частота помехи Fp.
Значения параметров приведены в таблице 2.
СОДЕРЖАНИЕ ОТЧЕТА
Отчет должен содержать:
6.1. Программу и результаты расчета фильтра с графиками АЧХ и ФЧХ,
6.2. Графики зависимости коэффициента прямоугольности фильтра от длины линии задержки и зависимости ослабления в полосе пропускания от длины линии задержки,
6.3. Результаты моделирования фильтра в виде временных диаграмм.
6.4. Выводы по работе.
Таблица 2
|
Номер бригады |
Значения параметров | |||
|
nv |
X |
Xp |
Fp, МГц | |
|
1 |
10 |
1 |
5 |
3 |
|
2 |
5 |
2 |
10 |
4 |
|
3 |
8 |
3 |
9 |
5 |
|
4 |
4 |
0,1 |
0,4 |
6 |
|
5 |
10 |
0,2 |
0,6 |
0,3 |
|
6 |
5 |
0,5 |
2 |
0,4 |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ РАБОТЫ
7.1. Синтез нерекурсивного цифрового фильтра рисунка 1 выполняется в программной среде Mathcad.

Рисунок 1 – Нерекурсивный фильтр с линейной ФЧХ
Введите значения частоты дискретизации Fd, граничной частоты фильтраFgи половины длины линии задержкиK=5 и рассчитайте коэффициенты системной функции фильтраbm
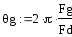
![]()
![]()

7.2.
Рассчитайте АЧХ и ФЧХ фильтра в диапазоне
нормированных частот fNот нуля доfN
max=0.5cшагом![]() .
.
Введите
значения fN
maxи![]()
Задайте диапазон изменения нормированной частоты
![]()
Определите зависимость комплексного коэффициента передачи от нормированной частоты
![]()

Введите
соотношения для АЧХ
![]() и ФЧХ
и ФЧХ![]()
![]()
![]()
Определите максимальное значение коэффициента передачи фильтра
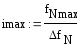
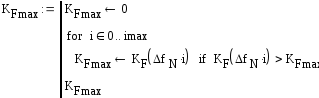
Постройте
график АЧХ (рисунок 2) в относительном
масштабе по оси ординат – зависимость
относительного коэффициента передачи
![]() от частоты
от частоты![]()

Рисунок
2 – Определение полосы пропускания
фильтра при неравномерности
![]()
(уровне 0.707)
На
графике проведите прямую, параллельную
оси абсцисс на уровне
![]() (при неравномерности коэффициента
передачи в полосе пропускания
(при неравномерности коэффициента
передачи в полосе пропускания![]() ).
Точка пересечения этой прямой с графиком
АЧХ определяет полосу пропускания
фильтра
).
Точка пересечения этой прямой с графиком
АЧХ определяет полосу пропускания
фильтра![]()
Постройте тот же график АЧХ, используя логарифмический масштаб по оси ординат (рисунок 3).
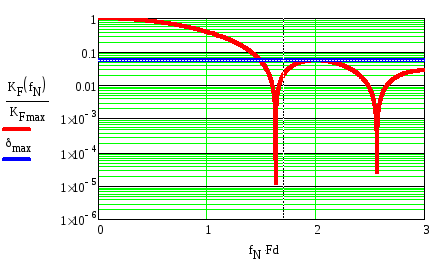
Рисунок 3 – Определение полосы пропускания фильтра при ослаблении A
в полосе задерживания
Измерьте
максимальный уровень пульсаций в полосе
задерживания фильтра
![]() и рассчитайте ослабление в полосе
задерживания
и рассчитайте ослабление в полосе
задерживания![]() .
.
Проведите
на графике АЧХ прямую, параллельную оси
абсцисс на уровне
![]() ,
и определите координату точки пересечения
этой прямой с АЧХ фильтра по оси абсцисс.
Координата этой точки определяет
полосу пропускания фильтра
,
и определите координату точки пересечения
этой прямой с АЧХ фильтра по оси абсцисс.
Координата этой точки определяет
полосу пропускания фильтра![]() при ослабленииA.
при ослабленииA.
Рассчитайте коэффициент прямоугольности фильтра
![]()
Повторите эксперимент для фильтра с окном Хемминга.
Для этого введите в программу функцию Хемминга
![]()
Рассчитайте новые значения коэффициентов bm
![]()
Скопируйте предыдущую программу, начиная с определения комплексного коэффициента передачи фильтра H(ΔfN).
Пронаблюдайте АЧХ и ФЧХ и рассчитайте новые значения ослабления в полосе задерживания A и коэффициента прямоугольности kp.
7.3. Чтобы снять зависимости коэффициента прямоугольности фильтра kp и ослабления в полосе задерживания AдБ от длины линии задержки повторите эксперимент при всех значениях K, указанных в таблицах 3 и 4. Рекомендуется при выбранном значении K определять сразу коэффициент прямоугольности и ослабление в полосе задерживания сначала для одного окна, затем для другого. После этого можно переходить к следующему значению K.
Запишите в отчет выводы о влиянии длины линии задержки на частоту пульсаций АЧХ, ослабление в полосе задерживания и коэффициент прямоугольности фильтра.
Таблица 3
|
Половина длины линии задержки K |
Коэффициент прямоугольности kp при прямоугольном окне |
Коэффициент прямоугольности kp при окне Хемминга |
|
5 |
|
|
|
10 |
|
|
|
15 |
|
|
|
20 |
|
|
|
25 |
|
|
Таблица 4
|
Половина длины линии задержки K |
Ослабление в полосе Задерживания AдБ при прямоугольном окне |
Ослабление в полосе Задерживания AдБ при окне Хемминга |
|
5 |
|
|
|
10 |
|
|
|
15 |
|
|
|
20 |
|
|
|
25 |
|
|
7.4. При моделировании фильтра воспользуемся схемой рисунка 1, но вместо отсчетов задержанного входного сигнала на выходах элементов задержки xn -1 …xn-2K , где индекс отражает номер отсчета входного сигнала, введем массив отсчетов v, где индекс, начиная с 1, определяет номер элемента задержки.

Рисунок 3 – Нерекурсивный цифровой фильтр с линейной ФЧХ с обозначением
выходных сигналов элементов задержки элементами массива v
Элементу задержки при графическом представлении алгоритма соответствует ячейка памяти вычислительного устройства при реализации фильтра, а номеру элемента задержки – адрес ячейки памяти. Содержимое ячейки памяти изменяется каждый интервал дискретизации. Массив x может быть как угодно большим в зависимости от времени действия сигнала, а размерность массива v определяется длиной линии задержки. Схема фильтра с новыми обозначениями приведена на рисунке 3.
Из схемы видно, что
![]() .
.
После определения отсчета выходного сигнала осуществляется сдвиг отсчетов сигнала в линии задержки, начиная с ее конца:
![]()
Для нахождения импульсной характеристики сформируйте единичный отсчет.
Для этого задайте максимальный номер отсчета nmax в интервале 150…250.
Введите диапазон изменения порядкового номера отсчета
![]()
Введите значение половины длины линии задержки K=25 и рассчитайте коэффициенты системной функции фильтра с прямоугольным окном
![]()
![]()
![]()
Введите программу фильтрации
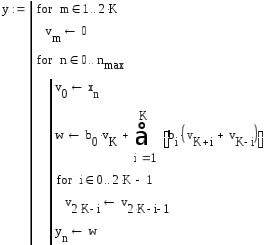
Поскольку выходной сигнал фильтра при действии на входе единичного отсчета и при нулевых начальных условиях представляет собой импульсную характеристику фильтра, то импульсная характеристика определится следующим соотношением
![]()
Для определения импульсной характеристики фильтра с оконной функцией Хемминга введите оконную функцию
![]()
Рассчитайте новые значения коэффициентов системной функции
![]()
Для определения выходного сигнала фильтра yn вновь введите программу фильтрации, а затем соотношение, определяющее импульсную характеристику
![]()
Постройте графики импульсных характеристик при прямоугольном окне hn и окне Хемминга hon.
Обратите внимание на симметрию импульсных характеристик и их отличие друг от друга.
Уменьшите длину линии задержки, установив K = 5, и вновь пронаблюдайте импульсные характеристики.
Запишите в отчет выводы о влиянии длины линии задержки на импульсные характеристики фильтров и об отличии импульсной характеристики фильтра с окном Хемминга от импульсной характеристики фильтра с прямоугольным окном.
7.5. Исследование селективных свойств фильтра начните с формирования полезного сигнала и помехи.
Сначала выполните моделирование счетчика отсчетов в элементарной посылке сигнала, содержащей nv отсчетов.
Задайте значение nv
Задайте начальное значение переменной счетчика
![]()
Определите n – ый отсчет счетчика и пронаблюдайте его временную диаграмму
![]()
![]()
Задайте максимальный уровень сигнала X и сформируйте случайную последовательность элементарных посылок сигнала
![]()
![]()
Пронаблюдайте временную диаграмму сигнала
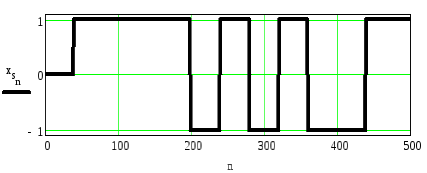
Сформируйте синусоидальную помеху
![]()
Задайте сумму сигнала и помехи
![]()
Задайте половину длины линии задержки
![]()
Рассчитайте коэффициенты системной функции фильтра
![]()
![]()
![]()
![]()
Определите выходной сигнал фильтра
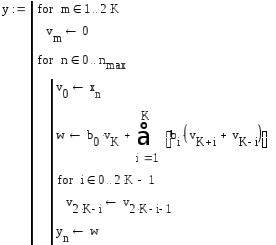
Пронаблюдайте временные диаграммы входного xn и выходного yn сигналов фильтра при K=5, 10, 15, 20, 25.
Запишите в отчет вывод о влиянии длины линии задержки на селективные свойства фильтра.
ПРИЛОЖЕНИЕ
к лабораторной работе №2
Синтез нерекурсивного цифрового фильтра методом ряда Фурье и «окна». Исследование
фильтра
1. Основные характеристики цифровых фильтров
Цифровым фильтром называется линейная частотно-избирательная система, реализуемая на основе вычислительного устройства.
Пусть при действии на входе цифрового фильтра последовательности отсчетов xn на выходе действует последовательность yn
Если n-ый отсчет выходного сигнала фильтра yn зависит только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени xn, xn-1 ..и т.д., то такой фильтр называется нерекурсивным.
Если n-ый отсчет выходного сигнала фильтра yn зависит не только от отсчетов входного сигнала в данный и предшествующие моменты дискретного времени xn, xn-1 и т.д., но и от отсчетов выходного сигнала в предшествующие моменты времени, то такой фильтр называется рекурсивным.
Импульсной характеристикой цифрового фильтра называется выходной сигнал фильтра при действии на его входе единичного отсчета и нулевых начальных условиях.
Фильтр с конечной импульсной характеристикой называется КИХ-фильтром (КИХ-конечная импульсная характеристика). Фильтр с бесконечной импульсной характеристикой называют БИХ-фильтром.
Системной функцией цифрового фильтра называется отношение Z-преобразования выходного сигнала фильтра к Z-преобразованию входного сигнала.
Известно [2], что выходной сигнал фильтра yn представляет собой дискретную свертку входного сигнала xn и импульсной характеристики hn
![]()
Воспользовавшись теоремой о дискретной свертке [2], выразим Z-преобразование Y(z) выходного сигнала фильтра yn через Z-преобразование X(z) входного сигнала xn
Y(z) = H(z) X(z),
где 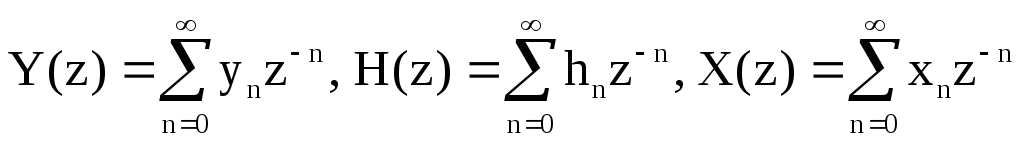 .
.
Из последних соотношений следует, что системная функция H(z) представляет собой Z-преобразование импульсной характеристики цифрового фильтра.
Комплексным
коэффициентом передачи фильтра
![]() является отношение комплексной амплитуды
является отношение комплексной амплитуды
![]() выходного сигнала фильтра к комплексной
амплитуде входного синусоидального
сигнала
выходного сигнала фильтра к комплексной
амплитуде входного синусоидального
сигнала![]()
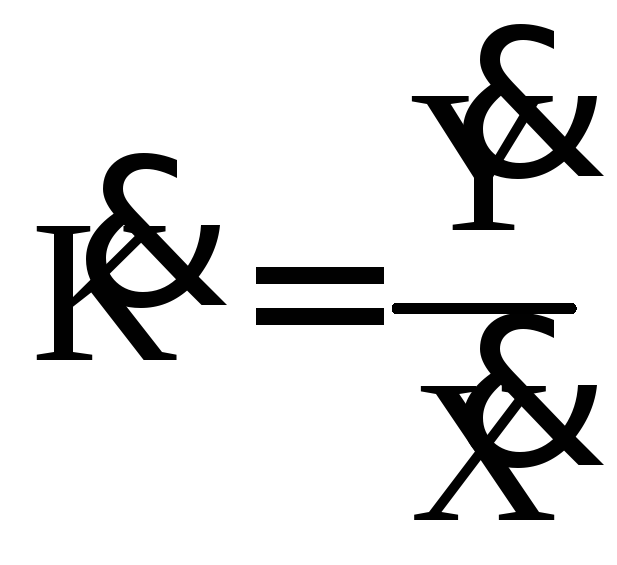 .
.
Коэффициентом передачи фильтра К называется модуль комплексного коэффициента передачи
![]()
Частотной
характеристикой цифрового фильтра
![]() называется зависимость комплексного
коэффициента передачи фильтра от
частоты.
называется зависимость комплексного
коэффициента передачи фильтра от
частоты.
Амплитудно-частотной
характеристикой (АЧХ)
![]() называется зависимость модуля комплексного
коэффициента передачи от частоты
называется зависимость модуля комплексного
коэффициента передачи от частоты
![]() .
.
Фазочастотной характеристикой (ФЧХ) называется зависимость аргумента комплексного коэффициента передачи фильтра от частоты.
![]() .
.
Для
нахождения комплексного коэффициента
передачи нужно в выражении для системной
функции заменить z
на
![]() :
:
![]() ,
,
где
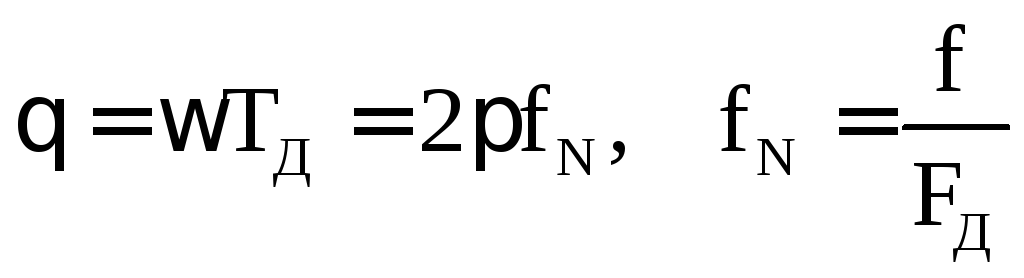 - нормированная частота – отношение
текущей частоты f
к частоте дискретизации FД.
- нормированная частота – отношение
текущей частоты f
к частоте дискретизации FД.
2. Нерекурсивный цифровой фильтр с линейной ФЧХ
На рисунке П.1 показан нерекурсивный фильтр, у которого коэффициенты системной функции b симметричны относительно середины линии задержки.
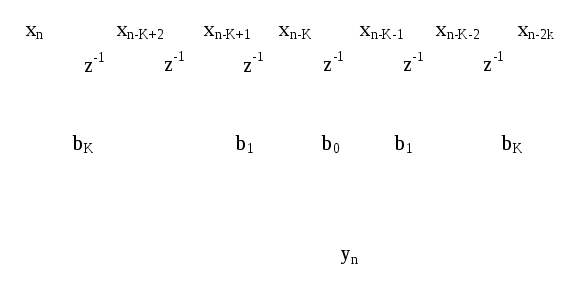
Рисунок П.1 – Нерекурсивный цифровой фильтр с линейной ФЧХ
Выходной сигнал фильтра определяется следующим соотношением
![]() .
.
Выразим Z – преобразование выходного сигнала фильтра через Z – преобразование входного сигнала
![]() .
.
Разделив Y(z) на X(z), найдем системную функцию
![]() .
.
Найдем
комплексный коэффициент передачи
фильтра, используя подстановку
![]() .
.
![]() .
.
Обозначим
![]() (П.1)
(П.1)
где

Тогда АЧХ и ФЧХ (без приведения в интервал от -π до π) фильтра определятся следующими соотношениями
![]() ,
(П.2)
,
(П.2)
![]() .
.
Так как второе слагаемое в выражении для ФЧХ - константа (0 или π), ФЧХ этого фильтра является линейно-ломаной.
Линейность ФЧХ обусловлена симметрией коэффициентов системной функции относительно середины линии задержки (симметрией импульсной характеристики фильтра).
3. Синтез нерекурсивного фильтра с линейной ФЧХ методом ряда Фурье и «окна»
Задачей
синтеза фильтра является определение
коэффициентов его системной функции
при заданных требованиях к АЧХ. В случае
фильтра с линейной ФЧХ и АЧХ, определяемой
рядом косинусов (П.1) и (П.2), этими
коэффициентами являются коэффициенты
![]() .
.
Из
(П.1) видно, что функция
![]() ,
определяющая АЧХ фильтра, является
периодической функцией с периодом 2π.
,
определяющая АЧХ фильтра, является
периодической функцией с периодом 2π.
Пусть требуется выполнить синтез ФНЧ, у которого функция A(θ) стремится к функции D(θ), показанной на рисунке П.2 в интервале изменения θ от –π до π.
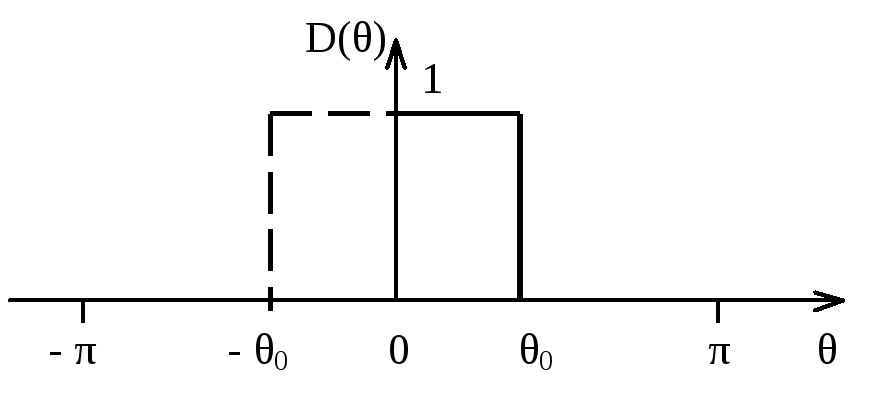
Рисунок П.2 – Идеальная АЧХ ФНЧ
Разложение функции D(θ) в ряд Фурье позволяет определить коэффициенты
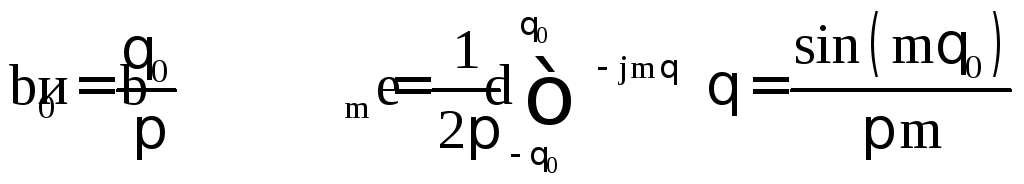 ,
(П.3)
,
(П.3)
где m = 1,2 ..K.
В
качестве примера приведем рассчитанные
по формулам (П.3), (П.1) и (П.2) функцию
![]() и АЧХ К(θ) при θ0
=
π / 2, K=3.
и АЧХ К(θ) при θ0
=
π / 2, K=3.
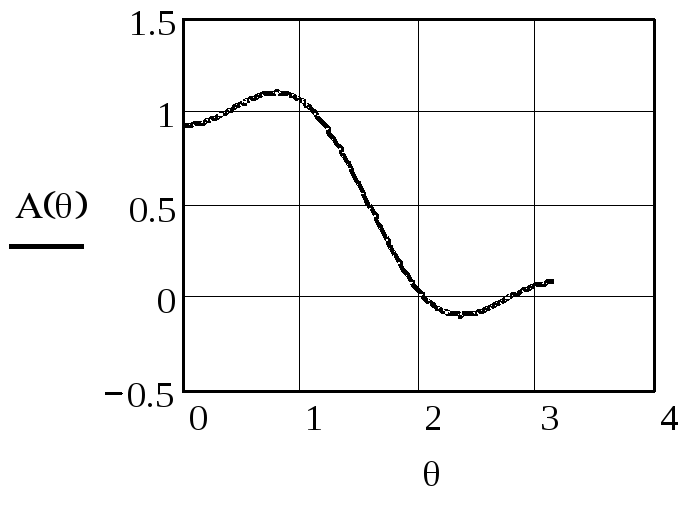
Рисунок
П.3 - Функция
![]() при θ0
=
π / 2, K=3
при θ0
=
π / 2, K=3
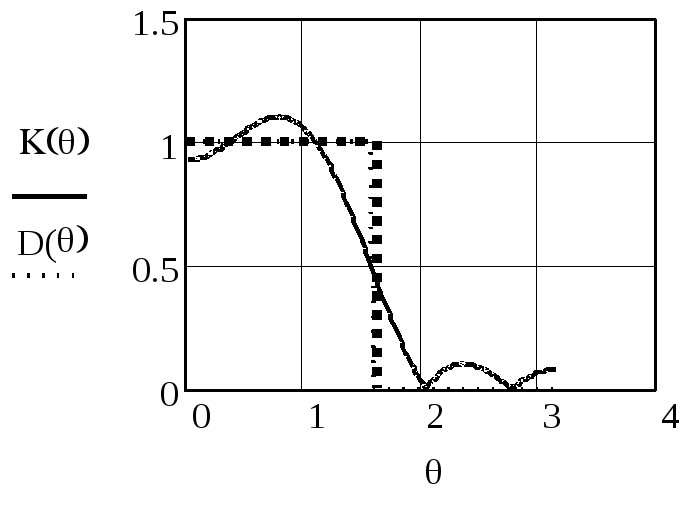
Рисунок П.4 –АЧХ К(θ) при θ0 = π / 2, K=3
Вместе с графиком реальной АЧХ K(θ) показана идеальная прямоугольная АЧХ D(θ). При K=3 эти характеристики сильно отличаются друг от друга. Особенностью АЧХ являются пульсации как в полосе пропускания, так и в полосе задерживания.
На рисунках П.5 и П.6 приведены АЧХ фильтров при K=10 и K=20 соответственно.
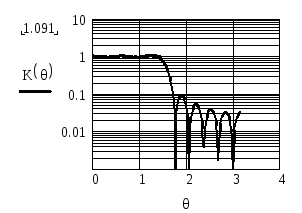
Рисунок П.5 – АЧХ фильтра с линейной ФЧХ при θ0 = π / 2, K = 10
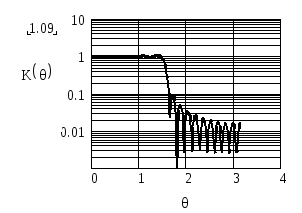
Рисунок П.6 – АЧХ фильтра с линейной ФЧХ при θ0 = π / 2,K= 20
На этих рисунках используется логарифмический масштаб по оси ординат для того, чтобы АЧХ была более наглядной в полосе задерживания.
Из рисунков видно, что увеличение длины линии задержки (уменьшение количества отбрасываемых членов разложения Фурье), делая АЧХ более прямоугольной, не устраняет пульсации АЧХ. С увеличением длины линии задержки частота пульсаций увеличивается, однако максимальный уровень первого бокового лепестка в полосе задерживания остается практически неизменным и равным 0.1.
Пульсации АЧХ вблизи точек разрыва функции, связанные с ограничением членов разложения в ряд Фурье, получили название явления Гиббса.
Для уменьшения пульсаций рядом специалистов по цифровой обработке сигналов было предложено использование так называемых «оконных функций».
Сущность метода состоит в следующем: вместо коэффициентов системной функции bm используют коэффициенты
![]() ,
,
где
![]() -m-ый
отсчет оконной функции.
-m-ый
отсчет оконной функции.
Простому ограничению ряда Фурье соответствует прямоугольное окно
![]()
Несколько других функций приведено в таблице П.1.
Таблица П.1 - Функции окна
|
Название окна |
Функция окна |
|
Окно фон Ганна (приподнятый косинус) |
|
|
Окно Хемминга |
|
|
Окно Блэкмана |
|
|
Окно Ланцоша |
|
На рисунках П.7 и П.8 показаны АЧХ рисунков П.5 и П.6 соответственно после операции сглаживания с использованием окна Хемминга. Из сопоставления АЧХ до сглаживания и после него видно, что эта операция приводит к существенному (примерно на 40 дБ) ослаблению пульсаций, но и к расширению переходной полосы между полосой пропускания и полосой задерживания фильтра.
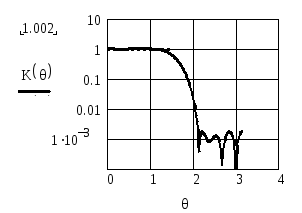
Рисунок П.7 – АЧХ фильтра при θ0 = π / 2, K=10 и сглаживанием пульсаций функцией
Хемминга
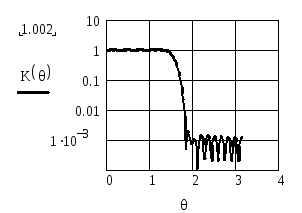
Рисунок П.8 – АЧХ фильтра при θ0 = π / 2, K=20 и сглаживанием пульсаций функцией
Хемминга
Описанный метод синтеза рассмотрен на примере фильтра нижних частот. Однако его нетрудно распространить на фильтры других типов.
Например, АЧХ полосового фильтра с граничными значениями полосы θ1 и θ2 можно представить в виде разности АЧХ ФНЧ, как это показано на рисунке П.9.
Такое представление АЧХ позволяет определить коэффициенты разложения в ряд Фурье bm как разность соответствующих коэффициентов разложений в ряд Фурье АЧХ ФНЧ
![]() .
.

Рисунок П.9 – Представление АЧХ полосового фильтра в виде разности АЧХ ФНЧ
D(θ)=D2(θ) – D1(θ)
Аналогичным образом находятся коэффициенты разложения для режекторного фильтра (РФ) и фильтра верхних частот (ФВЧ) соответственно
![]() ,
,
![]() .
.
РАБОТА №3
СИНТЕЗ НЕРЕКУРСИВНОГО ЦИФРОВОГО ФИЛЬТРА С ЛИНЕЙНОЙ ФЧХ
МЕТОДОМ НАИЛУЧШЕЙ РАВНОМЕРНОЙ АППРОКСИМАЦИИ

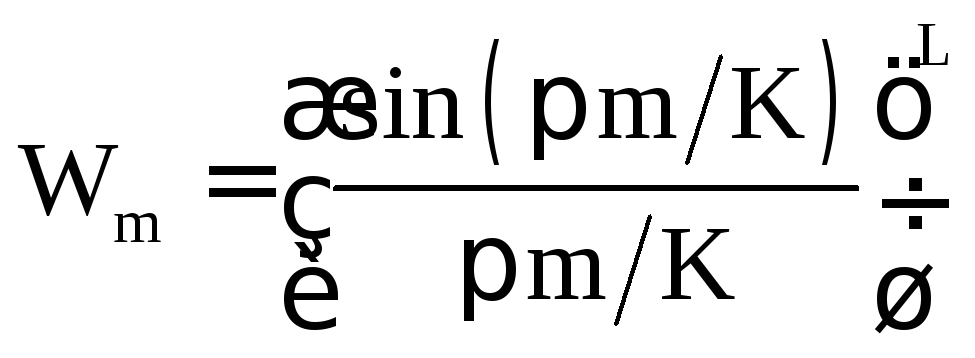 ,
где L - целое число
,
где L - целое число