Работа 2. Транспортная задача

1. Постановка задачи и ее математическая модель

Одна из традиционных постановок транспортной задачи сводится к следующему. В нескольких пунктах отправления (обозначим их A₁, A₂, … , A_m) имеются однотипные товары заданного объема. Известен их спрос в ряде пунктов назначения (обозначим их B₁, B₂, … , B_n), а также транспортные затраты по всем возможным маршрутам. Необходимо найти план перевозок, отвечающий требованию минимума совокупных транспортных затрат.

Для построения математической модели задачи, введем следующие обозначения:

а_i - объемы товаров в пунктах отправления A_i, i = 1, …, m, b_j – величина спроса в пунктах назначения (пунктах потребления) B_j, j = 1, …, n;

c_ij – затраты, связанные с перевозкой каждой единицы товаров по маршруту (i, j), связывающему пункт отправления A_i с пунктом назначения (или потребления) B_j;

x_ij – объем перевозки из пункта отправления A_i в пункт назначения B_j, а i = 1, …, m, j = 1, …, n.

Модель транспортной задачи содержать следующие элементы:

а) x_ij – переменные задачи, i = 1, …, m, j = 1, …, n;

б) ограничения задачи:

,

,

,

в) целевая функция – функция совокупных транспортных затрат (или издержек)

Тогда математическую модель задачи можно представить в виде

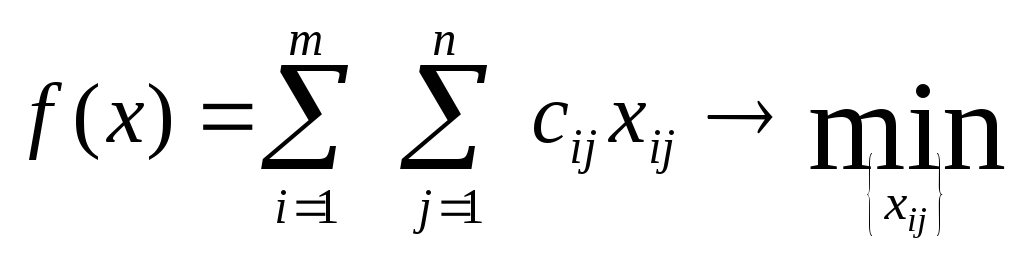. (1)

,

Если в последнем условии этой задачи имеет место равенство, то говорят о балансе спроса и предложения; когда его левая часть больше, чем правая, имеет место избыток; когда же правая часть больше, чем левая, имеет место дефицит. При решении задачи в последних двух случаях в модель задачи вводится фиктивный пункт потребления с присвоением ему спроса на величину

b_n+1 = , (2)

или фиктивного предложения на величину

a_m+1 = - (3)

соответственно. В результате этого задача вновь становится сбалансированной.

Одним из эффективных путей решения транспортной задачи и анализа ее результатов является метод потенциалов, являющийся разновидностью симплекс – метода, т. е. последовательность шагов алгоритма решения транспортной задачи с помощью метода потенциалов в точности повторяет последовательность этапов симплекс – алгоритма. После подготовки и ввода исходных данных (спрос и предложение, транспортные затраты по всем маршрутам), выполняются следующие этапы вычислений.

Этап 1. Построить начальный план перевозок, отвечающий требованиям по спросу и предложению (в терминах симплекс – метода этому соответствует построение начального базиса и базисного решения).

Этап 2. На основе условия оптимальности симплекс-метода среди всех небазисных переменных определить вводимую в базисное решение переменную; если все небазисные переменные удовлетворяют условию оптимальности, завершить вычисления, в противном случае перейти к следующему шагу;

Этап 3, С помощью условия допустимости симплекс - метода среди текущих базисных переменных определить исключаемую переменную, затем найти новое базисное решение и осуществить возвращение ко второму шагу.

Этап 1: определение начального базисного решения.

Существуют три процедуры нахождения начального базисного решения: правило северо-западного угла, метод наименьшей стоимости, метод Фогеля.

Проиллюстрируем работу алгоритма метода потенциалов на примере транспортной задачи, представленной в виде таблицы 1.

Таблица Т₀

	1	2	3	4
1	10 x11	2 x12	20 x13	11 x14	15
2	12 x21	7 x22	9 x23	20 x24	25
3	4 x31	14 x32	16 x33	18 x34	10
	5	15	15	15

Клетки этой таблицы соответствуют маршрутам, связывающим пунктs отправления (их три) с пунктами отправления (их четыре). В правой части таблицы указаны значения наличных грузов a_i, а внизу таблицы – спрос на эти товары b_j. В клетках указаны также соответствующие затраты c_ij. i = 1, … , m, j = 1 , … , n. Таким образом, а = (15, 25, 10)^Т – вектор предложения, b = (5, 15, 15, 15)^Т – вектор спроса, и условие баланса соблюдается

Для построения начального плана перевозок (начальное допустимое базисное решение) используют три способа: метод северо-западного угла, метод наименьшей стоимости, метод Фогеля.

Сущность метода «северо-западного угла» сводится к следующему.

а) Переменной x₁₁ присваиваем значение min (a₁, b₁) (в нашем случае - x₁₁ = 50);

б) Вычеркиваем строку или столбец с полностью реализованным предложением или с удовлетворенным спросом. В этой строке (столбце) мы не будем присваивать значения остальным переменным. Если одновременно удовлетворяется спрос и предложение, вычеркиваются только строка или столбец;

в) Если не вычеркнута только одна строка или только один столбец, процесс останавливается; в противном случае переходим к ячейке справа, если вычеркнут столбец, или к нижележащей ячейке, если вычеркнута строка. Затем возвращаемся к пункту а).

Так как в задаче имеется m + n - 1 независимых ограничений, то начальный план или начальное базисное решение состоит из m + n - 1 базисных переменных. По данным таблицы 1, в результате действия пунктов а) – в) получим x₁₁ = 5, x₁₂ = 10, x₂₂ = 5, x₂₃ = 15, x₂₄ = 5, x₃₄ = 10. Именно это начальное базисное решение и присутствует в таблице Т₁.

Таблица Т₁

	1	2	3	4
1	10	2	20	11	15
2	12	7	9	20	25
3	4	14	16	18	10
	5	15	15	15

Этап 2: определение вводимой и выводимой переменных по правилам симплексных преобразований.

В методе потенциалов каждой строке i и каждому столбцу j транспортной таблицы ставятся в соответствии числа (потенциалы) u_i и v_j, причем, для каждой базисной переменной x_ij эти потенциалы определяются из условий

u_i + v_j = c_ij. (4)

В данной задаче имеются 6 базисных переменных и 7 неизвестных потенциалов. Чтобы найти значение потенциалов из этой системы уравнений, нужно присвоить одному из них произвольное значение (обычно полагают u₁ = 0) и затем последовательно вычисляют значения остальных потенциалов.

Для базисных переменных:

x₁₁: u₁ + v₁ = 10; u₁ = 0, v₁ = 10;

x₁₂: u₁ + v₂ = 2; u₁ = 0, v₂ = 2;

x₂₂: u₂ + v₂ = 7; u₂ = 5, v₂ = 2;

x₂₃: u₂ + v₃ = 9; u₂ = 5, v₃ = 4;

x₂₄: u₂ + v₄ = 20; u₂ = 5, v₄ = 15;

x₃₄: u₃ + v₄ = 18; u₃ = 3, v₄ = 15.

Таким образом, u₁ = 0, u₂ = 5,u₃ = 3,v₁ = 10, v₂ = 2, v₃ = 4, v₄ = 15. Далее, используя вычисленные значения потенциалов, для каждой небазисной переменной вычисляются так называемые индексы по формуле

r_ij = u_i + v_j - c_ij. (5)

Для небазисных переменных:

x₁₃: u₁ + v₃ - c₁₃ = 0 + 4 – 20 = -16;

x₁₄: u₁ + v₄ - c₁₄ = 0 + 15 - 11 = 4;

x₂₁: u₂ + v₁ - c₂₁ = 5 + 10 - 12 = 3;

x₃₁: u₃ + v₁ - c₃₁ = 3 + 10 - 4 = 9:

x₃₂: u₃ + v₂ - c₃₂ = 3 + 2 - 14 = -9:

x₃₃: u₃ + v₃ - c₃₃ = 3 + 4 - 16 = -9.

Вычисленные значения индексов, вместе с нулевыми их значениями для базисных переменных (поскольку u_i + v_j - c_ij = 0 для любой базисной переменной х_ij) фактически являются коэффициентами так называемой Z – строки симплекс-таблицы (ее индексная строка). Представим их в виде

Индексная строка

базис	x11 x12 x13 x14 x21 x22 x23 x24 x31 x32 x33 x34
Z	0 0 -16 4 3 0 0 0 -9 -9 0

Поскольку в транспортной задаче целевая функция минимизируется, вводится в базисное решение переменная c наибольшим положительным коэффициентом в Z - строке. В данном случае вводимой переменной будет x₃₁. Все описанные выше вычисления обычно выполняются непосредственно в транспортной таблице, начиная с u₁ = 0, как это показано в таблице

Таблица Т₂

	v1=10	v2=2	v3=4	v4=15
u1=0	10 5	2 10	20 -16	11 4	15
u2=5	12 3	7 5	9 15	20 5	25
u3=3	4 9	14 -9	16 -9	18 10	10
	5	15	15	15

Итак, переменная x₃₁ вводится в базисное решение. Вопрос о том, какая переменная должна быть выведена из базисного решения (которая примет нулевое значение), решается следующим образом. Необходимо, чтобы перевозки по маршруту x₃₁ уменьшили общую стоимость перевозок. Для этой цели присвоим переменной x₃₁ некоторое значение x₃₁ = . Максимально возможное значение  определяется из следующих условий:

а) должны выполняться ограничения по спросу и предложению;

б) ни по какому маршруту не должны выполняться перевозки с отрицательным объемом грузов.

Построим замкнутый цикл, который начинается и заканчивается в ячейке (3, 1). Цикл состоит из горизонтальных и вертикальных отрезков, соединяющие ячейки, соответствующие текущим базисным переменным, и ячейку, соответствующую вводимой переменной. Для любой вводимой переменной можно построить только один замкнутый цикл. Эти действия приведены в Т₂.

Таблица Т₃

	v1=10	v2=2	v3=4	v4=15
u1=0	10 5	2 10	20 -16	11 4	15
u2=5	12 3	7 5	9 15	20 5	25
u3=3	4 9	14 -9	16 -9	18 10	10
	5	15	15	15

Теперь найдем . Для того чтобы удовлетворить ограничениям по спросу и предложению, надо поочередно отнимать и прибавлять  к значениям базисных переменных, расположенных в угловых ячейках цикла, как показано в таблице Т₃. При этом, не имеет значения направление обхода цикла: по часовой стрелке или против. Значения  должны отвечать условиям

x₁₁ = 5 -  ≥ 0;

x₂₂ = 5 -  ≥ 0;

x₃₄ = 10 -  ≥ 0,

откуда следует, что наибольшее значение  = 5. При этом будет иметь место x₁₁= x₂₂ =0. Из этих (теперь уже нулевых) переменных можно выбрать либо x₁₁, либо x₂₂ для исключения из базисного решения. Выберем для исключения переменную x₁₁.

Стоимость начального базисного решения составляет Z = 5х10 + 10х2 + 5х7 + 15х9 + 5х20 + 10х18 = 520 ед. Теперь суммарная стоимость перевозок будет на 9х5 = 45 единиц (9 = u₃+v₁ - c₃₁) меньше, т.е. 520 – 45 = 475 ед.

Определив x₃₁ = 5 и выбрав исключаемую переменную х₁₁, далее следует откорректировать значения базисных переменных, соответствующих угловым ячейкам замкнутого цикла: х₁₂ = 15, х₂₂ = 0, х₂₃ = 15, х₂₄ = 10, х₃₁ = 5, х₃₄ = 5. Скорректированные значения базисных переменных содержатся в таблице Т₄.

Теперь имеется новое базисное решение и улучшенное значение функции затрат, поэтому следует повторить вычисление потенциалов, т.е. перейти к этапу 2.

В таблице Т₄ представлены новые значения потенциалов, согласно которым новой вводимой в базис переменной будет x₁₄. По замкнутому циклу находим x₁₄ = 10 и исключаемую переменную x₂₄. Суммарные издержки теперь уменьшаются на величину 4х10 = 40 ед. (4 = u₁ + v₄ - c₁₄), т.е. 475 – 40 = 435 ед.

Результаты новой итерации представлены в таблице Т₅. Теперь новые значения величин u_i + v_j - c_ij для всех небазисных переменных x_ij отрицательные, что и является признаком оптимальности найденного базисного решения.

Таблица Т₄

	v1=1	v2=2	v3=4	v4=15
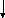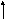u1=0	10 -9	2 15-	20 -16	19  4	15
u2=5	12 -6	7 0+	9 15	20 10 - 	25
u3=3	4 5	14 -9	16 -9	18 5	10
	5	15	15	15

Базисное Решение х₁₂ = 5, x₁₄ = 10, x₂₂ = 10, x₂₃ = 15, x₃₁ = 5, x₃₄ =5, составляет оптимальную искомую стратегию, а величина ед. составляет минимальные издержки.

Таблица Т₅

	v1= –3	v2=2	v3=4	v4=11
u1=0	10 -13	2 5	20 -16	11 10	15
u2=5	12 -10	7 10	9 15	20 -4	25
u3=7	4 5	14 -5	16 -5	18 5	10
	5	15	15	15

Отметим, в заключении, что так как метод потенциалов интерпретируется как симплекс-метод, то можно построить двойственную транспортную задачу. Она имеет вид:

максимизировать целевую функцию

(6)

при ограничениях

(7)

где u_i, v_j – свободные переменные: u_i – двойственная переменная, соответствующая ограничению на предложение пункта отправления A_i; v_j – двойственная переменная, соответствующая ограничению на спрос пункта B_j. Эту задачу можно представить в более привычной форме задачи линейного программирования

(8)

Когда новое целочисленное решение найдено, значение целевой функции для этого решения сравнивается с верхним значением (или нижним значением при минимизации). В начале работы алгоритма это значение принимается равным = -  ( = + ).