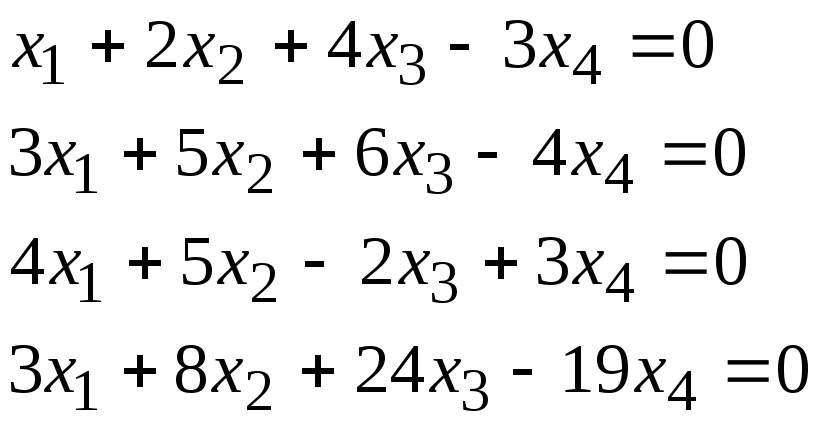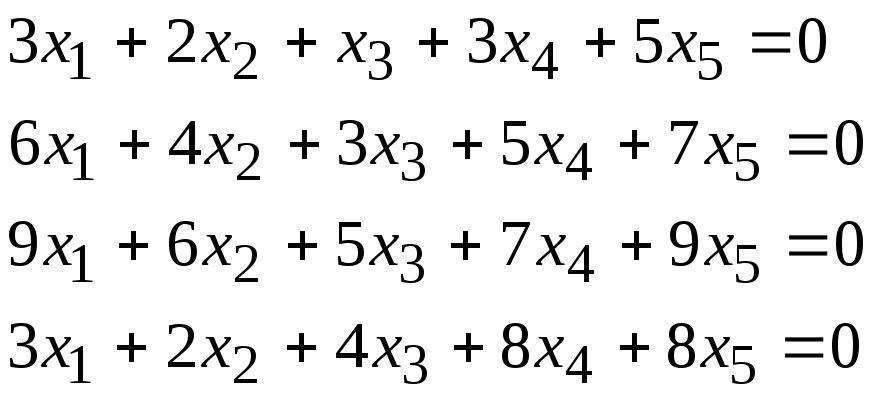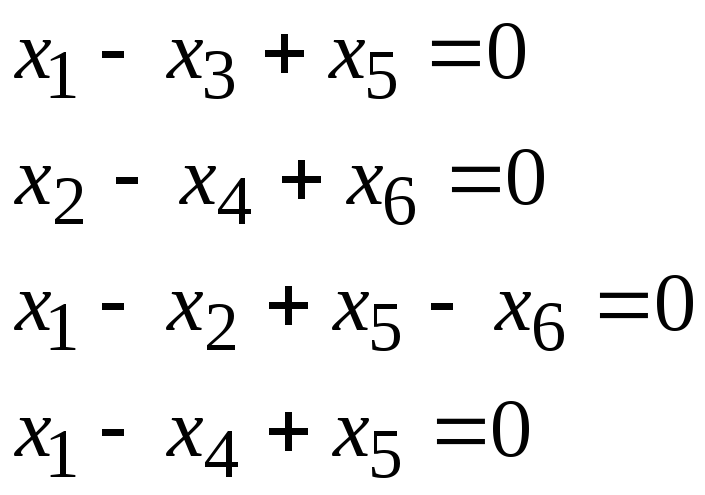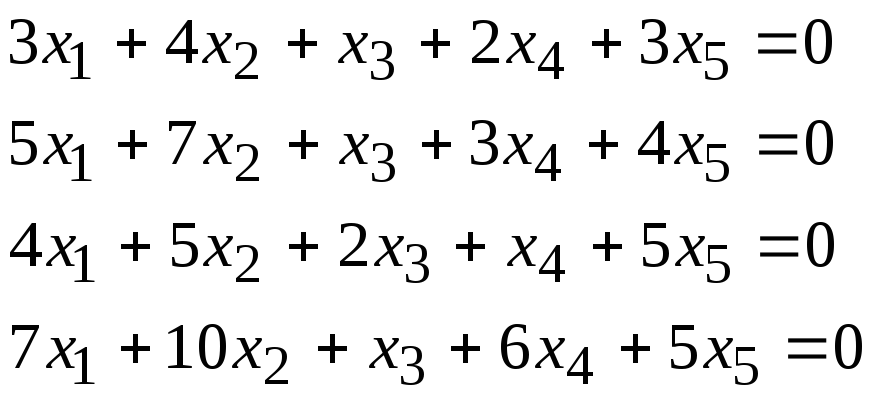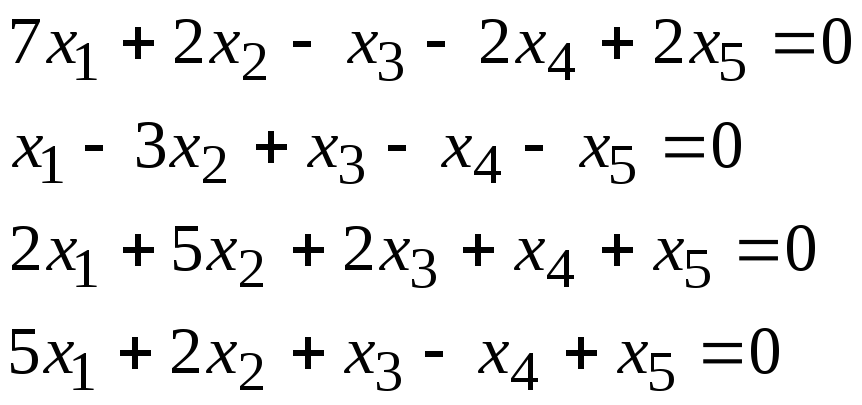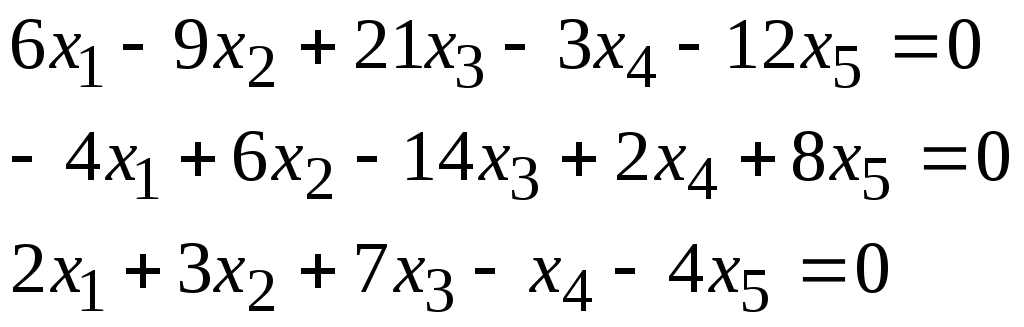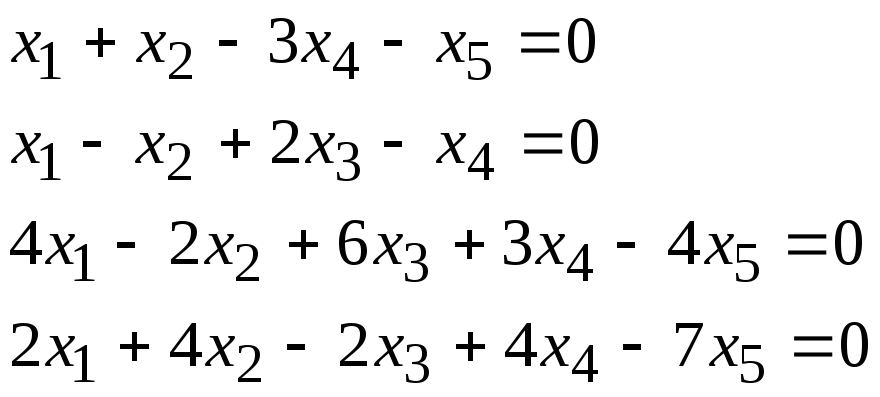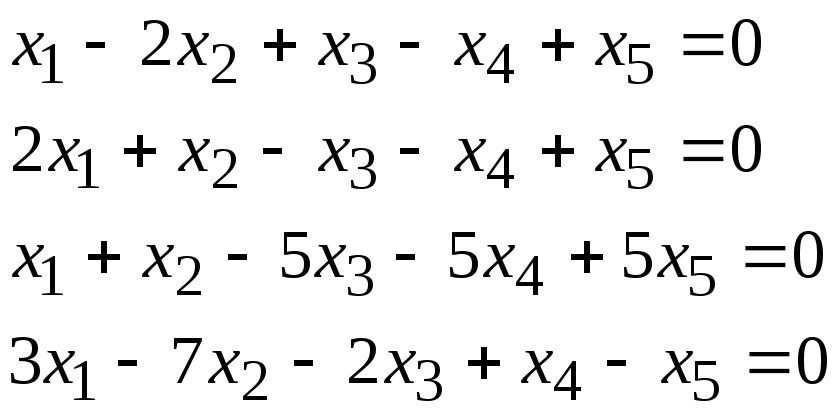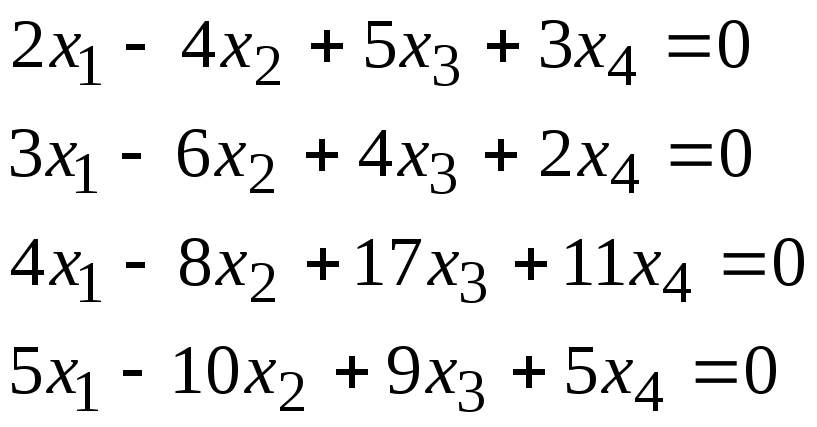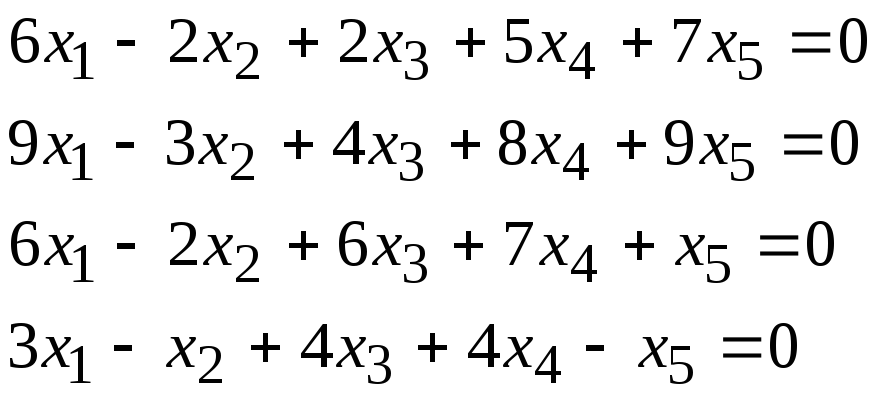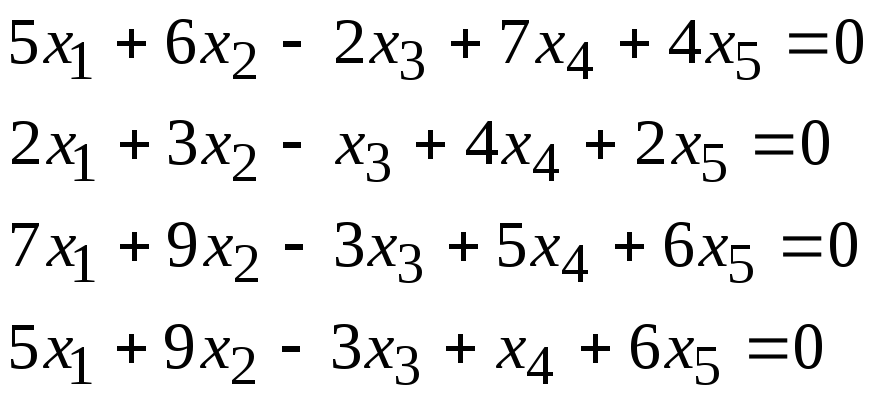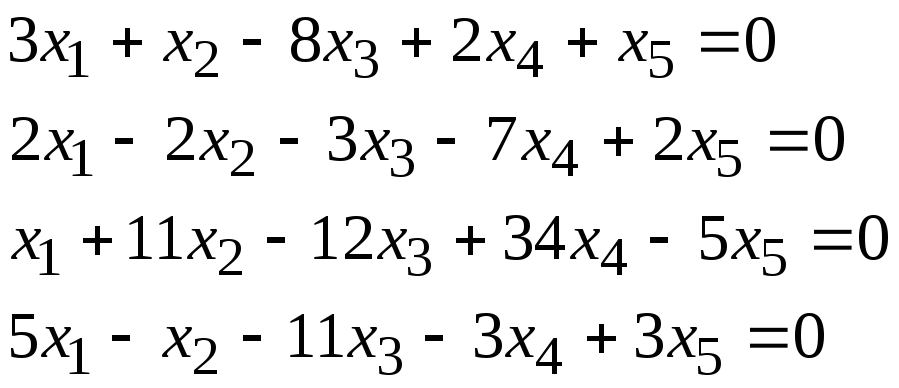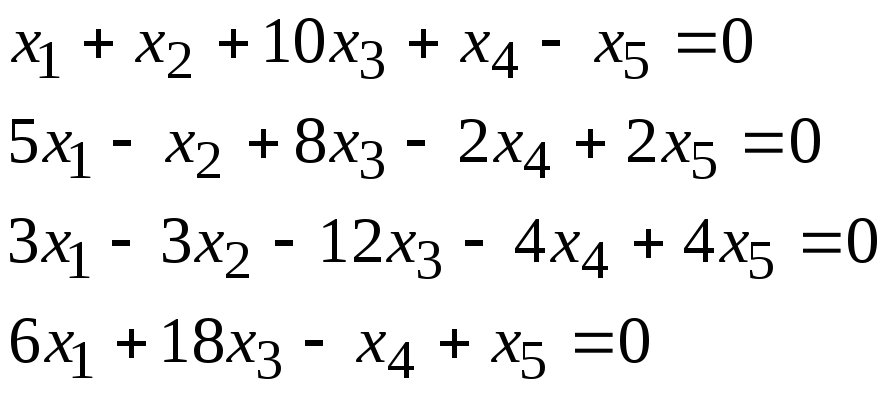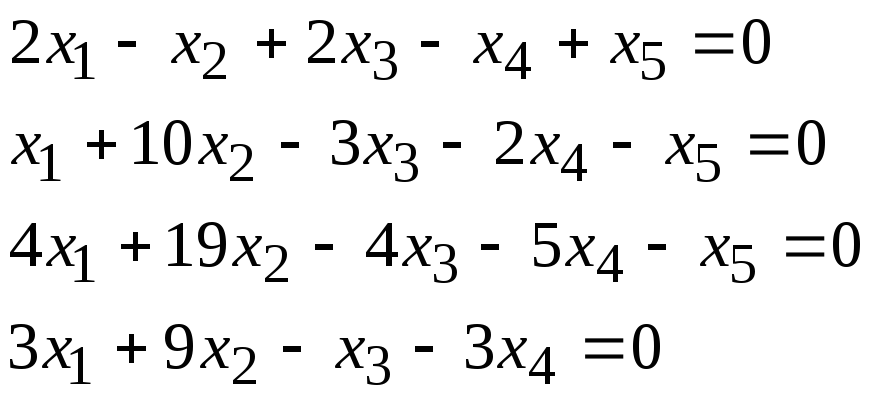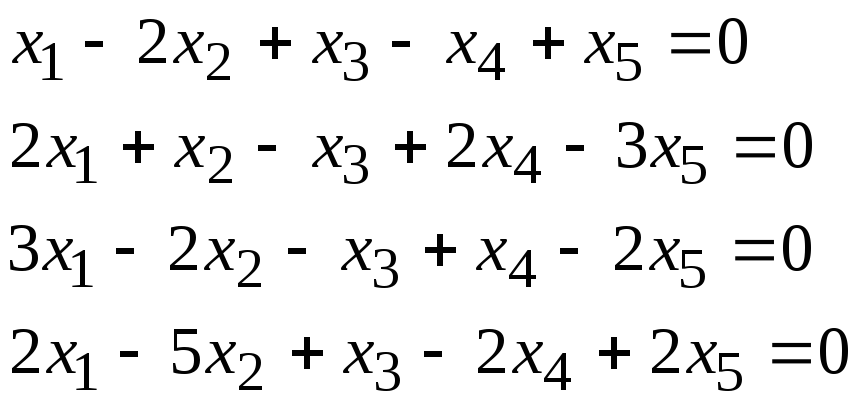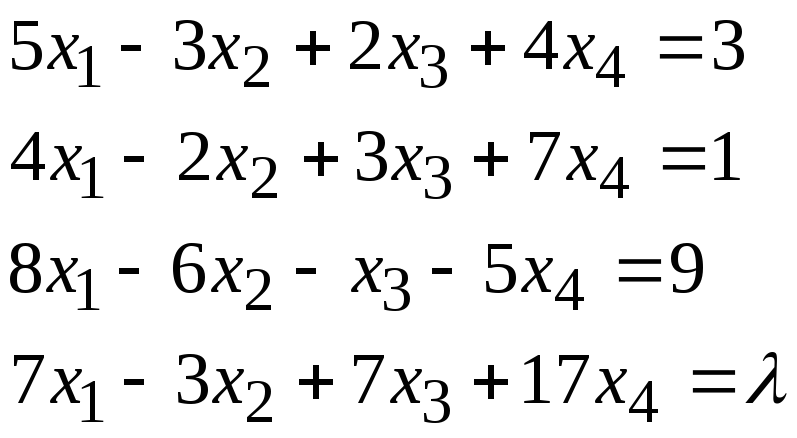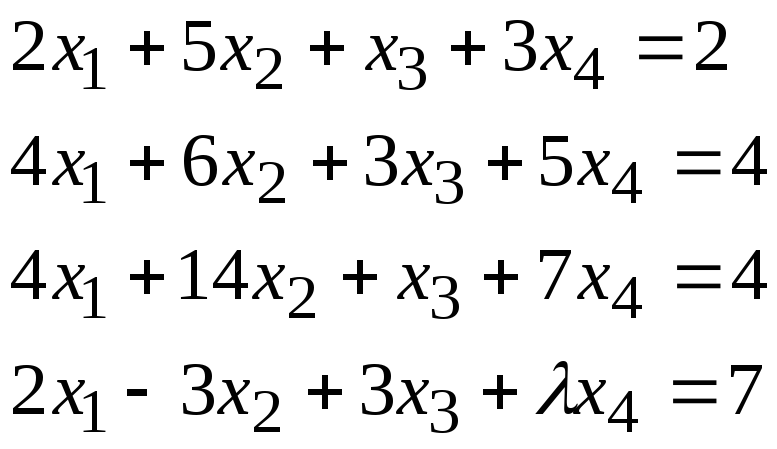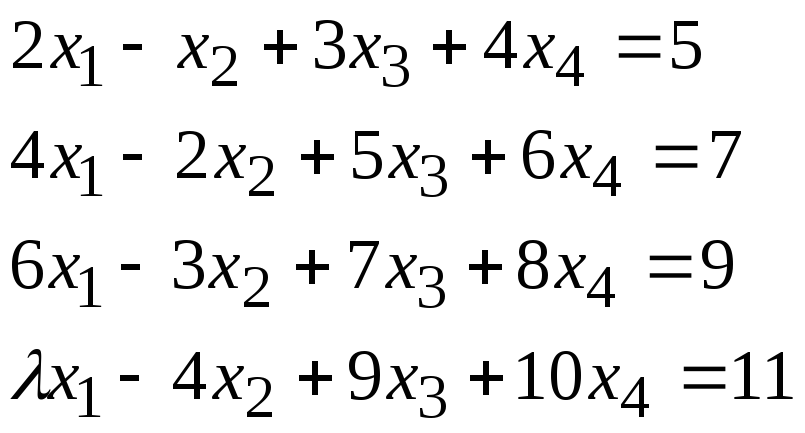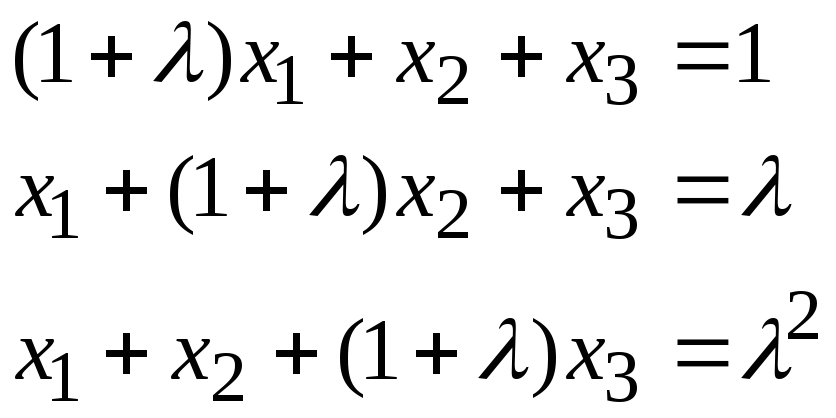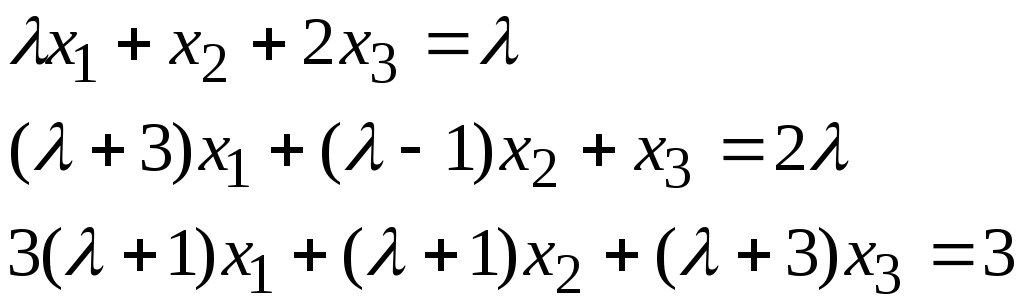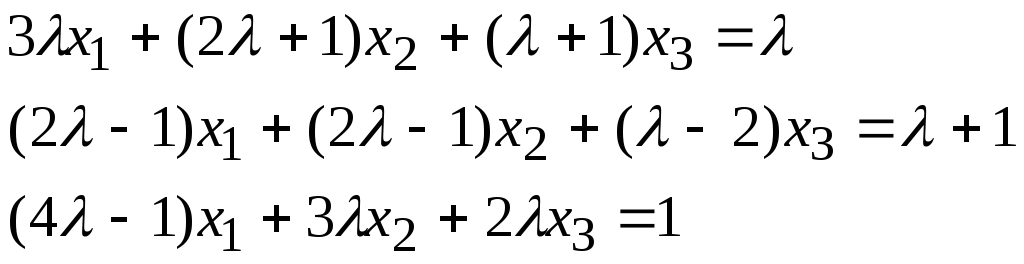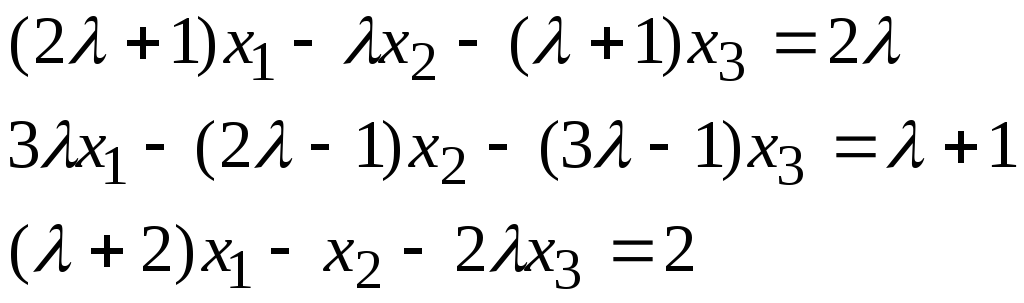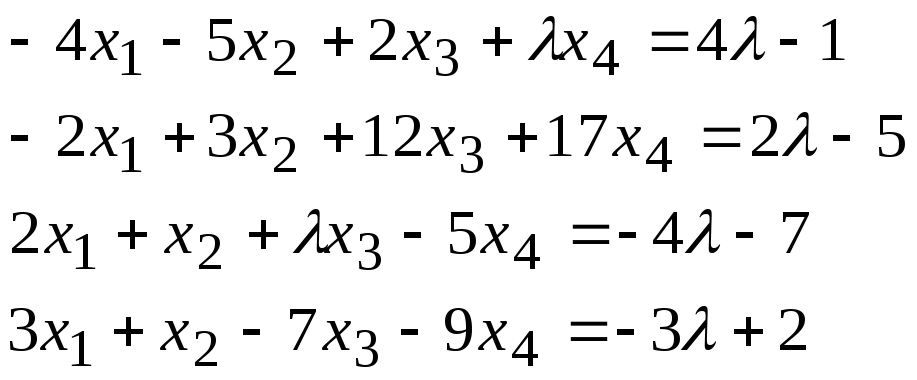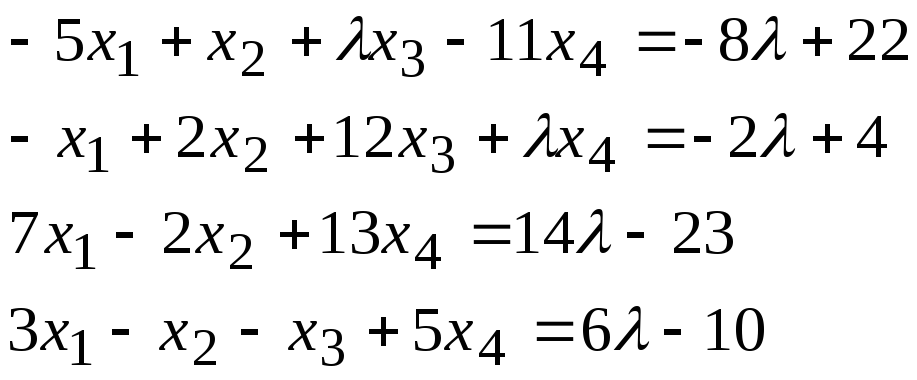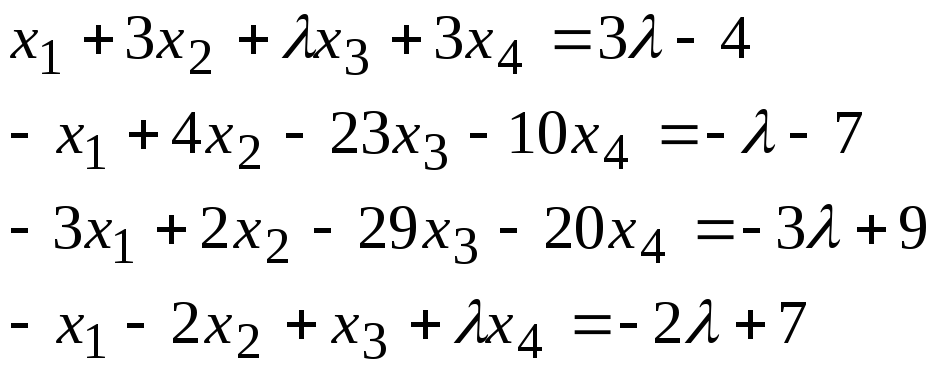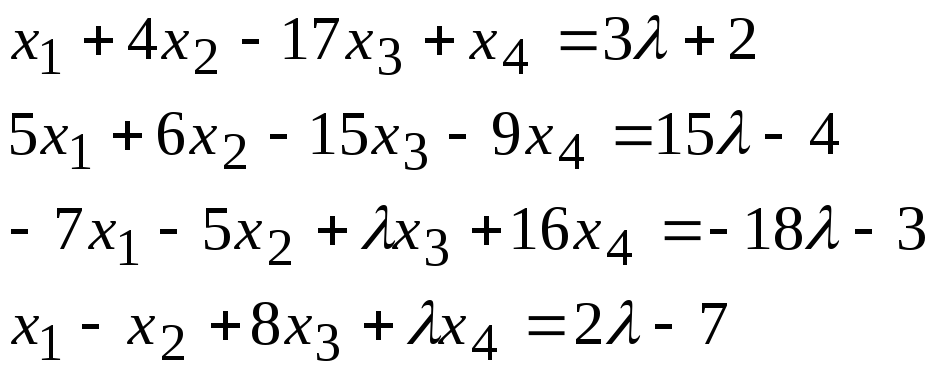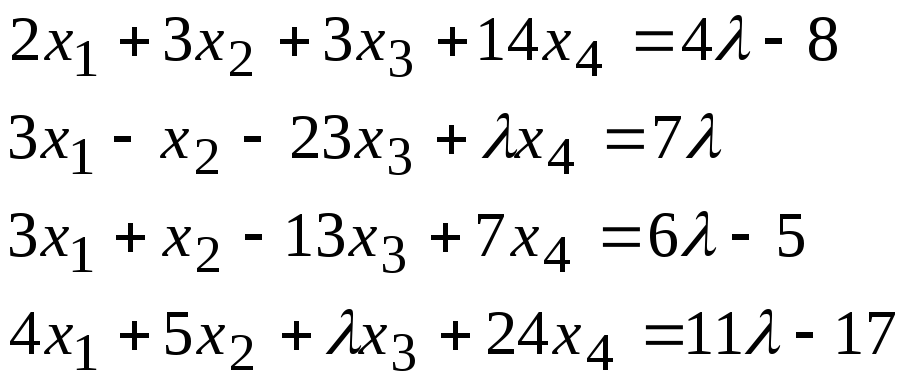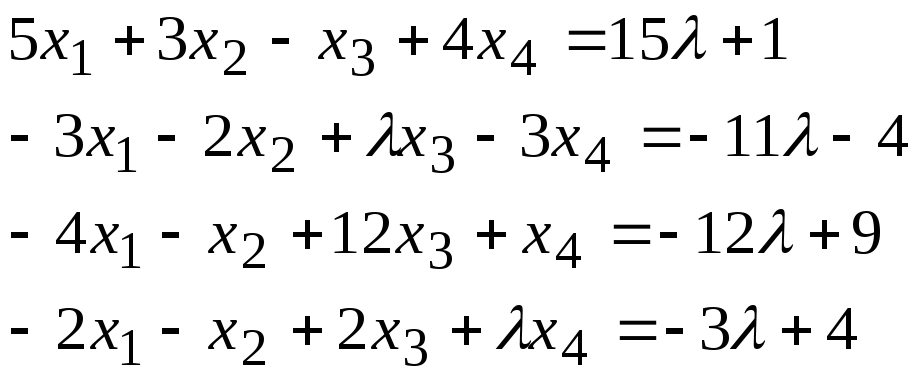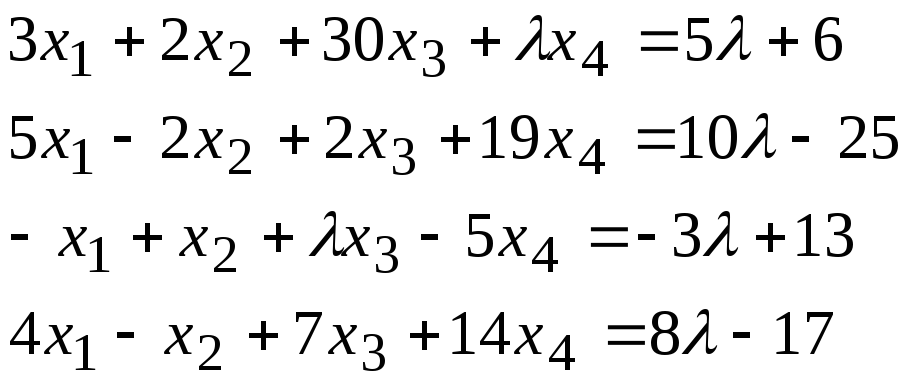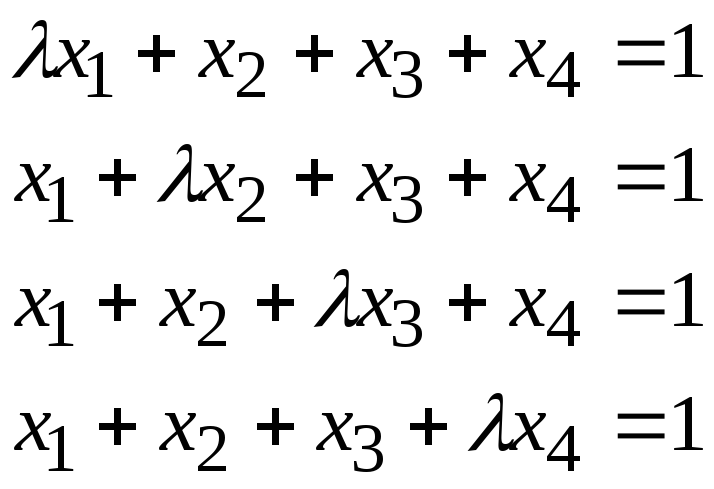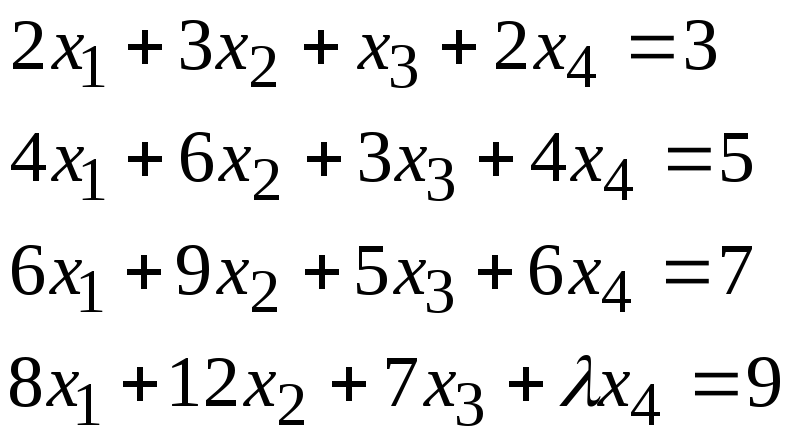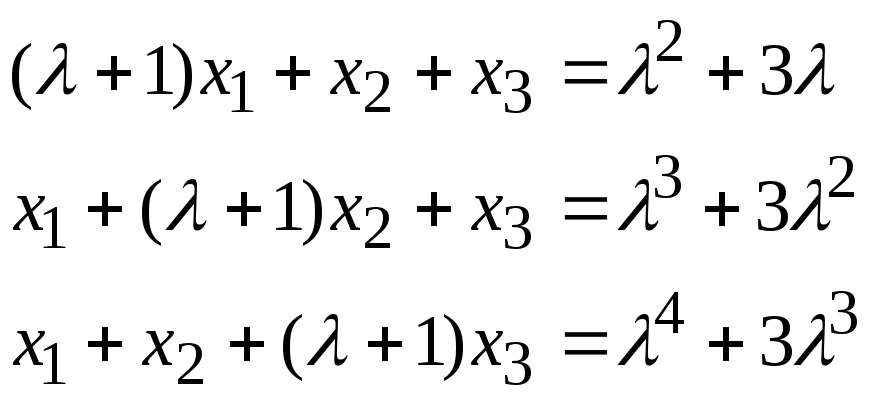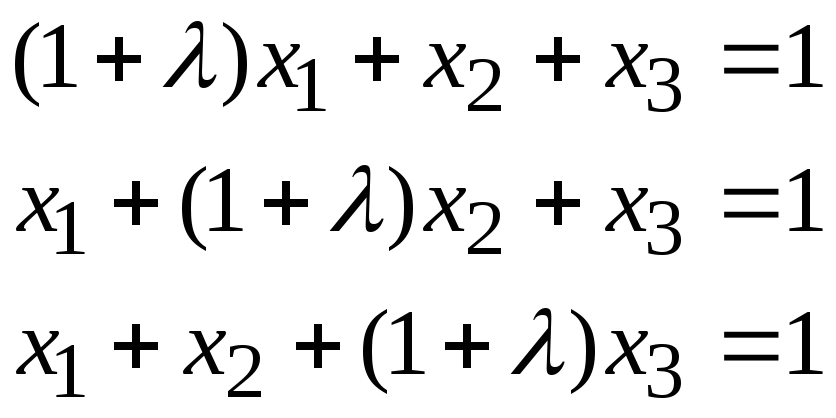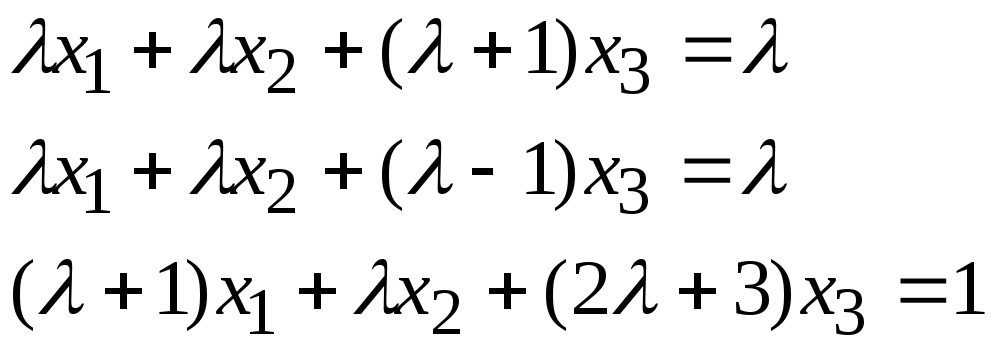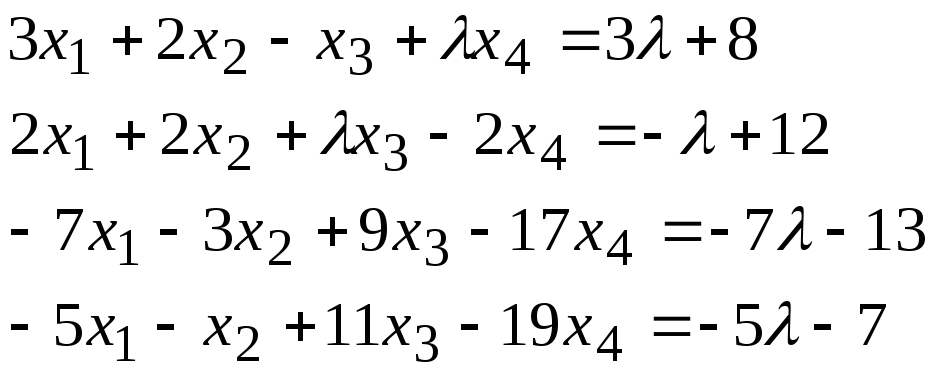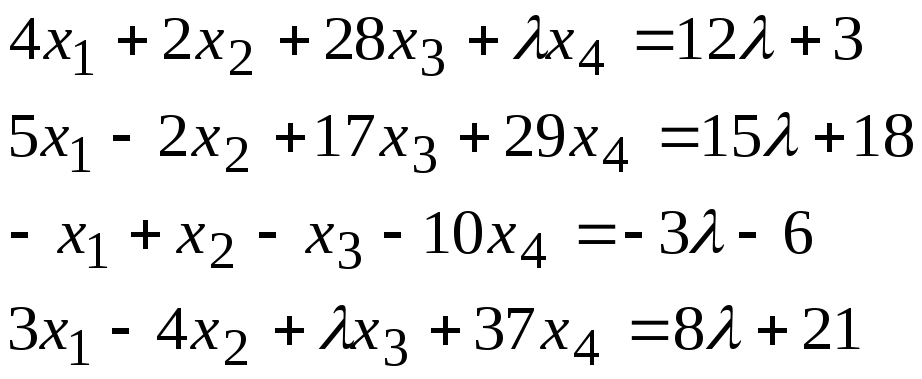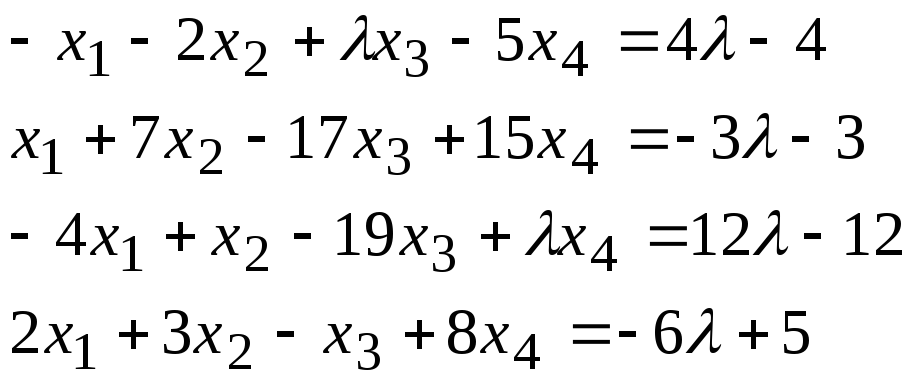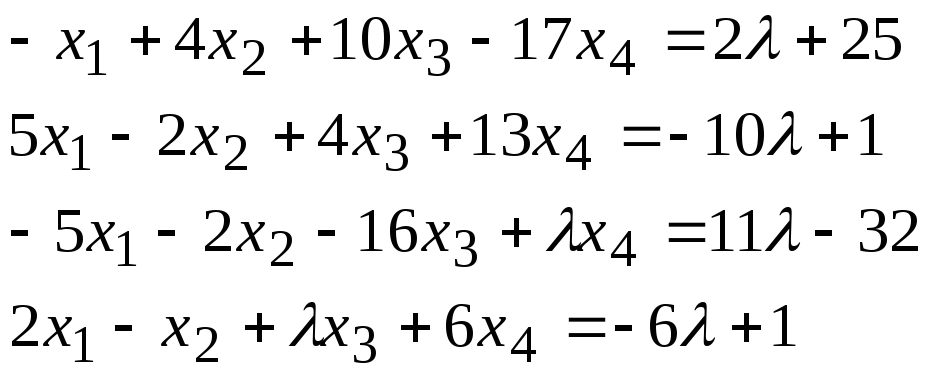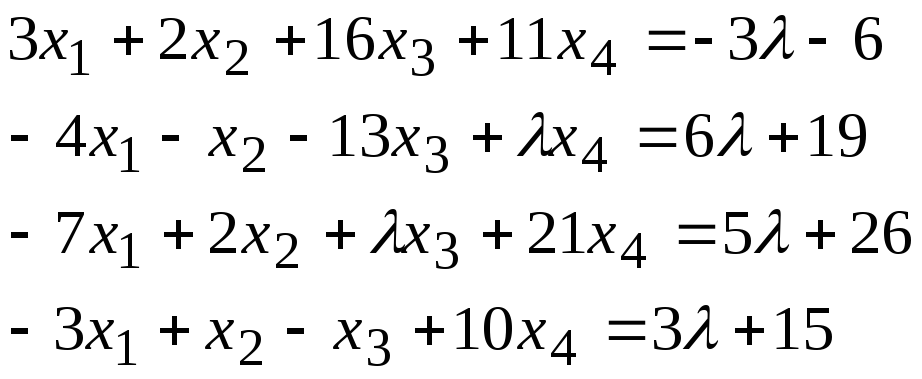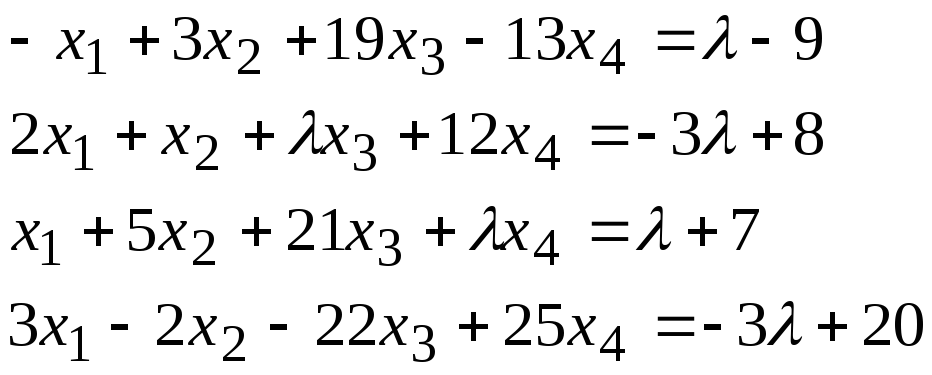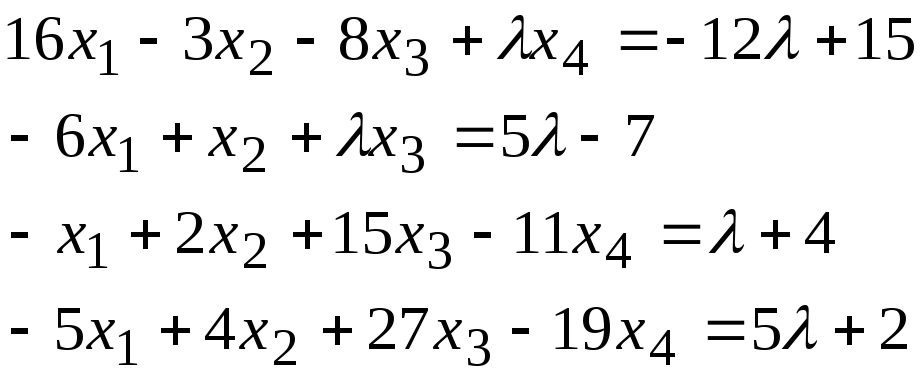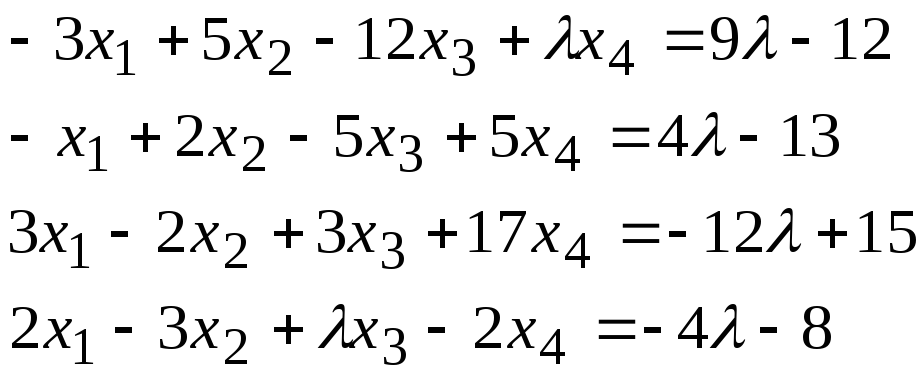- •А.В. Ряднов
- •Теоретические вопросы Типовой расчет №1 охватывает следующие темы:
- •Типовой расчет №2 охватывает следующие темы:
- •Указания по выполнению и сдаче типового расчета
- •Типовой расчет №1 Теоретические упражнения
- •Практические задания
- •Контрольные вопросы
- •1. Определители.
- •2. Комплексные числа и многочлены.
- •3. Алгебра матриц.
- •4. Линейные пространства.
- •Типовой расчет №2 Теоретические упражнения
- •Практические задания
- •Контрольные вопросы
- •5. Теория систем линейных уравнений.
- •6. Линейные операторы.
- •7. Билинейные и квадратичные формы.
- •8. Евклидовы пространства.
- •9. Линейные операторы в евклидовом пространстве.
- •Содержание
Практические задания
Задача 1. Найти фундаментальную систему решений и общее решение для однородной системы уравнений.
|
№ вар. |
Система уравнений |
|
1, 20 |
|
|
3, 22 |
|
|
5, 24 |
|
|
7, 26 |
|
|
9, 28 |
|
|
11, 30 |
|
|
13, 17 |
|
|
15, 19 |
|
|
2, 21 |
|
|
4, 23 |
|
|
6, 25 |
|
|
8, 27 |
|
|
10, 29 |
|
|
12, 16 |
|
|
14, 18 |
|
Задача 2*. Найти общее решение в зависимости от значения параметра. При каких значенияхсистема допускает решение с помощью обратной матрицы?
|
№ вар |
Система уравнений |
|
1 |
|
|
3 |
|
|
5 |
|
|
7 |
|
|
9 |
|
|
11 |
|
|
13 |
|
|
15 |
|
|
17 |
|
|
19 |
|
|
21 |
|
|
23 |
|
|
25 |
|
|
27 |
|
|
29 |
|
|
2 |
|
|
4 |
|
|
6 |
|
|
8 |
|
|
10 |
|
|
12 |
|
|
14 |
|
|
16 |
|
|
18 |
|
|
20 |
|
|
22 |
|
|
24 |
|
|
26 |
|
|
28 |
|
|
30 |
|
Задача 3.Линейный оператор![]() определяется
действием отображенияна концы радиус-векторов точек трехмерного
пространства.
определяется
действием отображенияна концы радиус-векторов точек трехмерного
пространства.
а)
Найти матрицу оператора
![]() в подходящем базисе пространства
в подходящем базисе пространства![]() ,
а затем в каноническом базисе
,
а затем в каноническом базисе![]() .
б) В какую точку трехмерного пространства
переходит точка с координатами (1, 0, 0)
под действием отображения?
.
б) В какую точку трехмерного пространства
переходит точка с координатами (1, 0, 0)
под действием отображения?
|
№ вар. |
Отображение |
|
1,21 |
отражение относительно плоскости x + y + z= 0
|
|
2,22 |
поворот на 180° вокруг оси x = y = z
|
|
3,23 |
проектирование на ось x = y/2 = z
|
|
4,24 |
проектирование на плоскость x + y + z = 0
|
|
5,25 |
отражение относительно плоскости x + y z= 0
|
|
6,26 |
поворот на 180° вокруг оси x=y=z
|
|
7,27 |
проектирование на ось 2x= 2y=z
|
|
8,28 |
проектирование на плоскость x y + z= 0
|
|
9,29 |
отражение относительно плоскости x y + z= 0
|
|
10,30 |
поворот на 180° вокруг оси x=y=z
|
|
11,16 |
проектирование на ось x= 2y= 2z
|
|
12,17 |
проектирование на плоскость x + y + z= 0
|
|
13,18 |
отражение относительно плоскости x + y + z= 0
|
|
14,19 |
поворот на 180° вокруг оси x=y=z
|
|
15,20 |
проектирование на плоскость x + y z= 0 |
Задача 4.а)
Доказать, что оператор![]() является линейным оператором в
пространстве
является линейным оператором в
пространстве![]() многочленов степени не вышеn.
многочленов степени не вышеn.
б) Найти его матрицу в каноническом базисе.
в) Существует ли обратный оператор? Если да, найдите его матрицу.
г) Опишите ядро
оператора
![]() ,
т. е. множество:
,
т. е. множество:
![]() .
.
|
№ вар. |
n |
|
|
1, 22 |
2 |
|
|
2, 23 |
2 |
|
|
3, 24 |
3 |
|
|
4, 25 |
3 |
|
|
5, 26 |
3 |
|
|
6, 27 |
3 |
|
|
7, 28 |
2 |
|
|
8, 29 |
3 |
|
|
9, 30 |
2 |
|
|
10, 16 |
2 |
|
|
11, 17 |
3 |
|
|
12, 18 |
2 |
|
|
13, 19 |
3 |
|
|
14, 20 |
2 |
|
|
15, 21 |
2 |
|
Задача 5.ПустьАматрица
оператора![]() из задачи 3 в каноническом базисе
из задачи 3 в каноническом базисе![]() .
Найдите собственные значения и собственные
векторы матрицыА. Объясните, как
полученный результат связан с
геометрическим действием оператора
.
Найдите собственные значения и собственные
векторы матрицыА. Объясните, как
полученный результат связан с
геометрическим действием оператора![]() .
.
Задача 6.Оператор![]() действует на матрицы, образующие линейное
подпространствоМв пространстве
матриц второго порядка.
действует на матрицы, образующие линейное
подпространствоМв пространстве
матриц второго порядка.
а) Доказать, что
![]() линейный оператор
вМ.
линейный оператор
вМ.
б) Найти матрицу
Аоператора![]() в каком-нибудь базисе пространстваМ.
в каком-нибудь базисе пространстваМ.
в) Найти собственные
значения и собственные векторы оператора
![]() (напомним, что в этой задаче векторами
являются матрицы).
(напомним, что в этой задаче векторами
являются матрицы).
г) Доказать, что
![]() оператор простого
типа, описать его действие в собственном
базисе.
оператор простого
типа, описать его действие в собственном
базисе.
|
№ вар. |
|
|
B |
|
1, 16 |
y = u |
|
|
|
2, 17 |
y = u |
|
|
|
3, 18 |
x + v = 0 |
|
|
|
4, 19 |
x + v = 0 |
|
|
|
5, 20 |
x + y + u + v = 0 |
|
|
|
6, 21 |
x y + u + v = 0 |
|
|
|
7, 22 |
x + y u v = 0 |
|
|
|
8, 23 |
x 2y u v = 0 |
|
|
|
9, 24 |
y = u |
|
|
|
10, 25 |
y = u |
|
|
|
11, 26 |
x + v = 0 |
|
|
|
12, 27 |
x + y + u + v = 0 |
|
|
|
13, 28 |
x + y + 2u + v = 0 |
|
|
|
14, 29 |
x + y + 2u v = 0 |
|
|
|
15, 30 |
x + y v = 0 |
|
|
Задача 7.В
пространстве![]() геометрических векторов с обычным
скалярным произведением векторы базиса
геометрических векторов с обычным
скалярным произведением векторы базиса![]() заданы координатами в базисе
заданы координатами в базисе![]() .
.
а) Найдите матрицу
Грама
![]() скалярного произведения в этом базисе.
Выпишите формулу для длины вектора
через его координаты в базисеS.
скалярного произведения в этом базисе.
Выпишите формулу для длины вектора
через его координаты в базисеS.
б) Ортогонализуйте базис S. Сделайте проверку ортонормированности построенного базисаPдвумя способами:
1) выписав координаты векторов из Pв каноническом
базисе
![]() ;
;
2) убедившись, что преобразование матрицы Грамма
при переходе от
базиса Sк базисуP(по формуле![]() )
приводит к единичной матрице.
)
приводит к единичной матрице.
|
№ вар. |
1, 23 |
2, 24 |
3, 25 |
|
|
1 1 1 2 1 0 0 1 1 |
1 0 1 1 1 1 2 1 0 |
1 1 0 1 1 1 1 0 2 |
|
№ вар. |
4, 26 |
5, 27 |
6, 28 |
|
|
1 0 2 2 1 1 1 1 0 |
0 1 2 1 1 1 2 0 1 |
1 1 1 2 0 1 1 1 2 |
|
№ вар. |
7, 29 |
8, 30 |
9, 16 |
|
|
2 0 1 1 1 1 1 2 1 |
1 1 1 1 1 1 2 0 1 |
2 0 1 1 1 1 2 0 1 |
|
№ вар. |
10, 17 |
11, 18 |
12, 19 |
|
|
1 1 0 2 0 1 1 1 1 |
1 0 1 2 1 1 1 1 0 |
2 1 0 1 1 1 1 0 1 |
|
№ вар. |
13, 20 |
14, 21 |
15, 22 |
|
|
1 0 2 1 1 1 1 2 0 |
1 1 0 2 1 1 1 0 1 |
1 1 1 1 1 1 2 1 0 |
Задача 8. Задана квадратичная форма.
а) Привести ее к каноническому виду методом Лагранжа, записав соответствующее преобразование переменных.
б) Привести ее к каноническому виду ортогональным преобразованием.
в) Проверить закон инерции квадратичной формы на примерах преобразований, полученных в пунктах а), б).
|
№вар. |
Квадратичная форма |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|