
- •Введение
- •Глава I. Основы линейной алгебры
- •1. Матрицы и действия над ними
- •2. Определители второго и третьего порядка. Обратная матрица
- •3. Системы линейных алгебраических уравнений
- •Формулы Крамера
- •3.2 Матричный способ решения системы линейных алгебраических уравнений
- •4. Метод Гаусса решения произвольных систем линейных алгебраических уравнений
- •5. Собственные числа и собственные векторы матрицы
- •Глава 2. Элементы векторной алгебры и аналитической геометрии. Комплексные числа
- •1. Элементы векторной алгебры и аналитической геометрии в пространстве
- •2. Аналитическая геометрия на плоскости
- •3. Линии второго порядка
- •4. Полярная система координат
- •5. Комплексные числа
- •Глава 3. Введение в анализ. Дифференциальное исчисление функции одной переменной.
- •Задачи для контрольных работ
- •Контрольная работа № 3 Введение в анализ. Дифференциальное исчисление функции одной переменной
2. Аналитическая геометрия на плоскости
Общее уравнение прямой на плоскости имеет вид
![]() ,
где
,
где
![]() .
.
Вектор
![]() ,
перпендикулярный прямой, называетсянормальным
вектором прямой на плоскости.
,
перпендикулярный прямой, называетсянормальным
вектором прямой на плоскости.
Уравнение вида
![]() ,
где
,
где![]() ,
,![]() ,
,![]() ,
называетсяуравнением
прямой с
угловым коэффициентом.
,
называетсяуравнением
прямой с
угловым коэффициентом.
Уравнение прямой,
проходящей через данную точку![]() с заданным
угловым коэффициентом,
имеет вид:
с заданным
угловым коэффициентом,
имеет вид:
![]() .
.
Угол между прямыми
![]() ,
,![]() определяется
следующим образом:
определяется
следующим образом:
![]() .
.
Задание 2.
Даны уравнения двух высот треугольника
![]() и
и![]() ,
и одна из вершин
,
и одна из вершин![]() .
Составить уравнения сторон треугольника.
Сделать чертеж.
.
Составить уравнения сторон треугольника.
Сделать чертеж.
Решение.
По условию задачи нам известны:
![]() ,CD:
,CD:
![]() и BE:
и BE:
![]() .
Определим уравнение стороныAB.
Высота CD
перпендикулярна стороне AB,
а потому их угловые коэффициенты
.
Определим уравнение стороныAB.
Высота CD
перпендикулярна стороне AB,
а потому их угловые коэффициенты
![]() и
и![]() удовлетворяют условию:
удовлетворяют условию:![]() .
Из уравнения прямойCD
следует, что
.
Из уравнения прямойCD
следует, что
![]() .
Тогда
.
Тогда![]() .
.![]()
Напишем уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом:
![]() .
.
Подставив в это
уравнение координаты точки А и угловой
коэффициент
![]() ,получим
уравнение стороны АВ:
,получим
уравнение стороны АВ:
![]()
или
![]() .
.
Аналогично можно
получить и уравнение стороны АС.
Действительно, в силу перпендикулярности
ВЕ и АС имеем:
![]() .
Из уравнения высоты ВЕ следует, что
.
Из уравнения высоты ВЕ следует, что
![]() .
Тогда
.
Тогда![]() .
Следовательно, подставив в уравнение
прямой, проходящей через данную точку
с заданным угловым коэффициентом,
координаты точкиА
и угловой коэффициент
.
Следовательно, подставив в уравнение
прямой, проходящей через данную точку
с заданным угловым коэффициентом,
координаты точкиА
и угловой коэффициент
![]() ,
получим уравнение стороныАС:
,
получим уравнение стороныАС:
![]()
или
![]() .
.
Теперь составим уравнение стороны ВС. Для этого определим координаты вершин В и С треугольника АВС. Координаты точки В можно определить из условия пересечения прямых АВ и ВЕ:
![]() .
.
Решение полученной
системы и есть координаты вершины![]() ,
а именно
,
а именно![]() .
.
Таким же образом определяем координаты точки С:
![]()
и тогда С![]() .
.
Уравнение прямой, проходящей через точки В и С, имеет вид :
![]() ,
,
где B![]() ,
C
,
C![]() .
.
Подставив координаты точек В и С в данное уравнение, получим уравнение стороны ВС:
![]()
или
![]() .
.
Сделаем теперь чертеж:
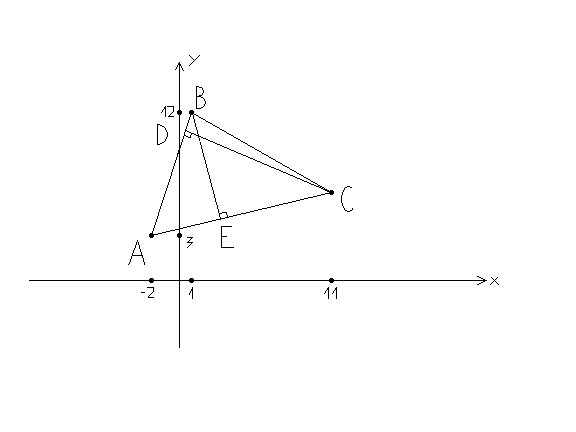
3. Линии второго порядка
К линиям второго порядка относят окружность, эллипс, гиперболу и параболу.
Каноническое
![]() уравнение
окружности
имеет вид
уравнение
окружности
имеет вид
![]() ,
,
где r- радиус окружности.
Каноническое
уравнение эллипса
имеет вид ![]()
где
![]()
![]() .
.
Каноническое уравнение гиперболы имеет вид
![]() ,
,
где
![]() .
.
Каноническое уравнение параболы имеет вид
а)
![]() , где
, где
![]() >
0 ( парабола симметрична относительно
оси
>
0 ( парабола симметрична относительно
оси![]() );
);
б)
![]() (парабола симметрична относительно
оси
(парабола симметрична относительно
оси![]() ).
).
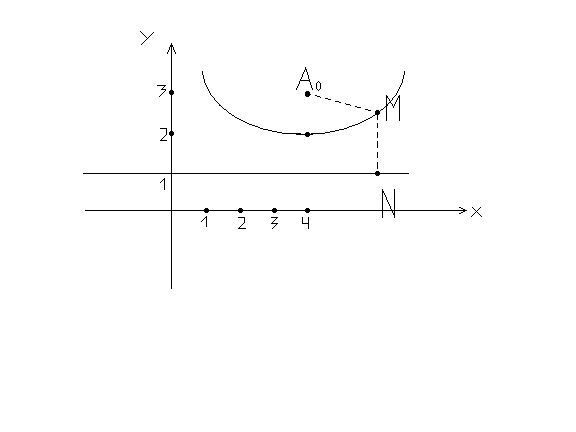
Задание
3. Составить уравнение линии, каждая
точка которой одинаково удалена от
точки
![]() и прямой
и прямой![]() .
Сделать чертеж.
.
Сделать чертеж.
Решение
Пусть М (x,
y)
– любая точка искомой линии,
![]() -
основание перпендикуляра, опущенного
из точки
-
основание перпендикуляра, опущенного
из точки![]() на прямуюy
на прямуюy![]() .
Тогда точка
.
Тогда точка
![]() имеет координаты
имеет координаты![]() .
Расстояние от точкиМ
до прямой
.
Расстояние от точкиМ
до прямой
![]() есть расстояние между точкамиМ
и N:
есть расстояние между точкамиМ
и N:
![]()
![]()
![]() .
.
Теперь определим
расстояние между точками М
и
![]() :
:
![]() .
.
По условию задачи
![]()
![]() .
Следовательно, для любой точки
.
Следовательно, для любой точки![]() справедливо равенство:
справедливо равенство:
![]()
или
![]() .
.
Окончательно,
![]() .
.
Полученное уравнение
является уравнением параболы с вершиной
в точке
![]() .
Действительно, сделаем замену
.
Действительно, сделаем замену
![]() .
.
Тогда уравнение примет вид:
![]()
(каноническое уравнение параболы ).
4. Полярная система координат
Говорят, что на плоскости введена полярная система координат, если заданы:
некоторая точка 0, называемая полюсом;
некоторый луч, исходящий из точки 0 и называемый полярной осью.
Полярными
координатами точки
M
называются два числа: полярный
радиус
![]() иполярный
угол
иполярный
угол
![]() - угол между полярной осью и вектором
- угол между полярной осью и вектором![]() .
.
Пусть на плоскости введены декартова и полярная системы координат, причем начало декартовой системы совпадает с полюсом, а полярная ось - с положительной полуосью абсцисс. Тогда прямоугольные координаты x, y точки М и ее полярные координаты ρ, φ связаны следующими формулами:
![]() ,
,
![]()
![]() ,
,
![]()
Задание 4.
Линия задана уравнением
![]() в полярной системе координат. Требуется:
в полярной системе координат. Требуется:
Построить линию по точкам, придавая φ значения от
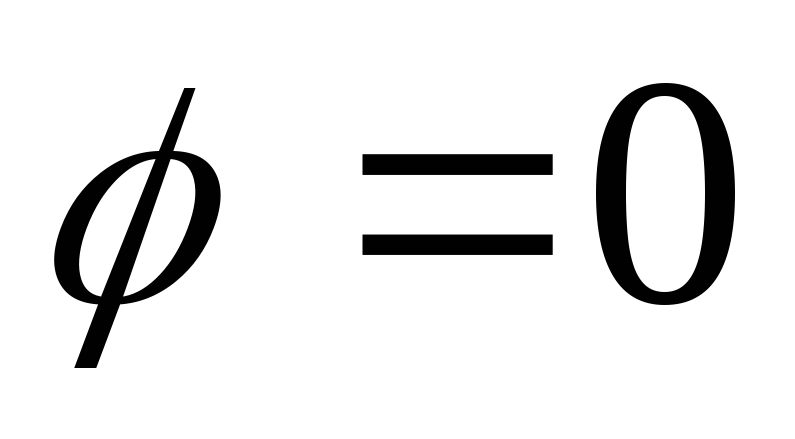 до
до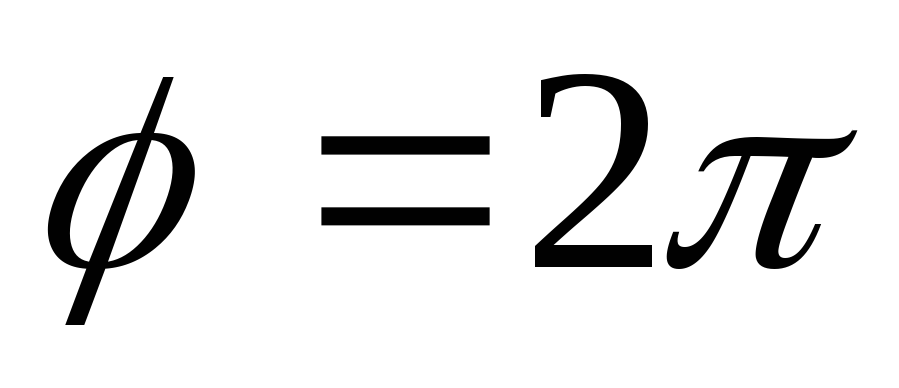 через промежуток
через промежуток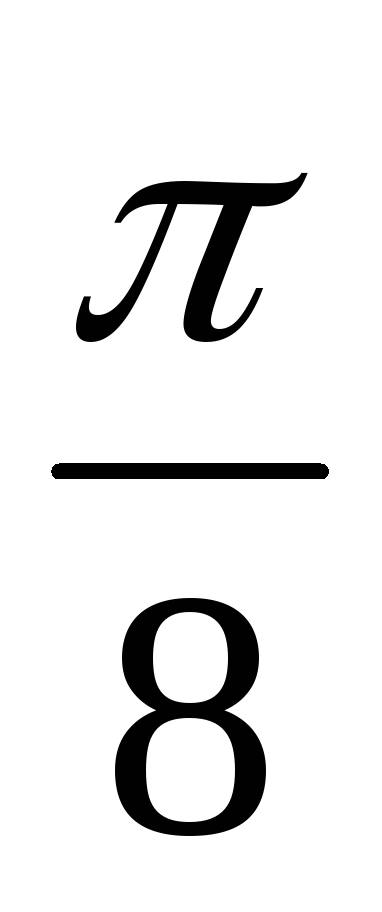 .
.Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.
По уравнению в декартовой прямоугольной системе координат определить тип линии.
Решение.
1) Совместим
декартову и полярную системы координат
и рассмотрим окружность произвольного,
достаточно большого радиуса
![]() с
центром в полюсе. Построим радиусы,
образующие углы
с
центром в полюсе. Построим радиусы,
образующие углы![]() с полярной осью, где
с полярной осью, где![]() принимает значения от
принимает значения от![]() до
до![]() с шагом
с шагом![]() .
Вычислим косинусы этих углов и по этим
значениям найдем
.
Вычислим косинусы этих углов и по этим
значениям найдем![]() .
Результаты вычислений занесем в таблицу:
.
Результаты вычислений занесем в таблицу:
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,92 |
0,7 |
0,38 |
0 |
-0,38 |
-0,7 |
-0,92 |
-1 |
-0,92 |
-0,7 |
-0,38 |
0 |
0,38 |
0,7 |
0,92 |
1 |
|
|
0,16 |
0,17 |
0,19 |
0,24 |
0,33 |
0,53 |
1,11 |
4,16 |
∞ |
4,16 |
1,11 |
0,53 |
0,33 |
0,24 |
0,19 |
0,17 |
0,16 |
Построим точки
(![]() )
и по полученным точкам построим искомую
линию:
)
и по полученным точкам построим искомую
линию:

2) Найдем уравнение данной линии в декартовой системе координат. Для этого воспользуемся формулами:
![]() .
.
Отсюда
![]() ,
,![]()
![]() .
.
Тогда имеем:
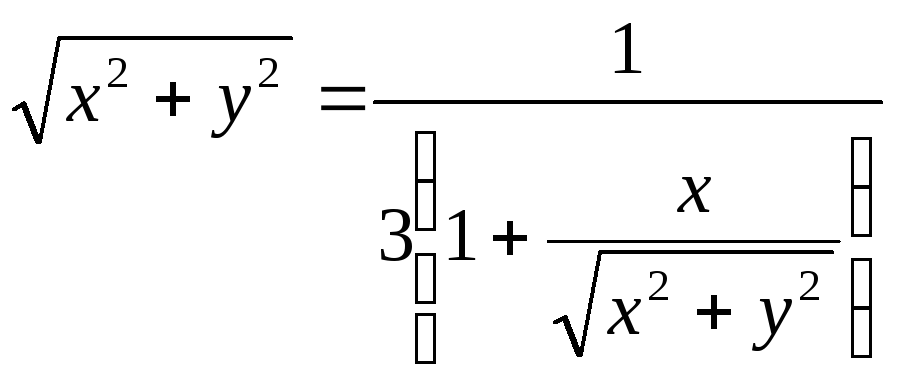
или после упрощения
![]() .
.
Чтобы определить тип линии, определяемой полученным уравнением,
преобразуем его к каноническому виду:
![]()
или
![]() .
.
Окончательно получим:
![]() ,
,
где
![]() ,
,![]() .
Таким образом, данное уравнение определяет
параболу.
.
Таким образом, данное уравнение определяет
параболу.
