1. Непрерывная случайная величина

Функция распределения: F(x) = P(X < x)

F’(x) = f(x) – функция плотности вероятностного распределения (она положительная и площадь трапеции под графиком этой функции = 1)

2. Нормальное вероятностное распределение

EX = a

DX = σ²

13. Функция распределения и ее свойства

Функция распределения — функция, характеризующая распределение случайной величины (вероятность того, что случайная величина примет меньшее значение)

P(X < x) = P(A)

Свойства:

1. Функция распределения есть неубывающая функция

2. На минус бесконечности функция распределения равна нулю F(-∞) = 0

3. На плюс бесконечности функция распределения равна единице F(+∞) = 1

прерывная (ступенчатый график)

равномерная (график y=kx+b)

14. Эмпирическая функция распределения

Эмпирическая функция распределения – полученная на опыте

n_x – одно из наблюдаемых значений

n – сумма выборки (сумма всех наблюденных значений)

Свойства:

Значения эмпирической функции принадлежат отрезку [0,1].

Она неубывающая функция.

Если – наименьшее наблюдаемое значение , то F(X) = 0 при , если – наибольшее, то F(X) = 1 при .

15. Полигон и гистограмма

Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки .

В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала – сумму частот вариант, попавших в i–й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению . (аналог функции плотности вероятностного распределения). Площадь одного прямоугольника - вероятность

16. Функция плотности вероятностного распределения и ее свойства

Производная от функции распределения – функция плотности вероятностного распределения.

Свойства:

1. Площадь прямоугольника на графике функции = 1

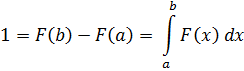
2. f(x) – неотрицательная функция т.е. f(x) ≥ 0;

17. Биномиальное распределение

Биномиальное распределение - распределение количества «успехов» в последовательности из N независимых случайных экспериментов, таких что вероятность «успеха» равна p, а неудачи - q.

биномиальное распределение – появляется в схеме независимых испытаний Бернулли – в каждом опыте либо успех (p) либо неудача (q)

0

1

…

n

- опыты

C вероятностью:

Где - – биномиальный коэффициент.

EX = np

DX = npq

0 < p < 1

q = 1 – p

18. Теорема и распределение Пуассона

Распределение Пуассона - это частный случай биномиального распределения для редких событий)

0

1

…

n

с вероятностью: (теорема Пуассона: если n устремить к ∞, а p к 0, тогда для любого k вероятность получить успех при n испытаниях по схеме Бернулли стремится к этой формуле)

EX = λ

DX = λ

19. Нормальное вероятностное распределение

нормальное вероятностное распределение – куполообразный график

EX = a

DX = σ²

20. Равномерное распределение

Непрерывное равномерное распределение характеризуются тем, что вероятность любого интервала зависит только от его длины

21. Локальная предельная теорема Муавра-Лапласа

Предельные теоремы – совокупность теорем, говорящих о том, что все распределения сводятся к нормальному.

Локальная предельная теорема.

Есть биномиально распределенная случайная величина (берется из схемы Бернулли (схема независимых испытаний, успех – p, неудача – q)). Тогда вероятность того, что в событие A при n испытаниях появится точно m раз, стремится к нормальному распределению:

где ; .

22. Интегральная предельная теорема Муавра-Лапласа

Интегральная предельная теорема:

Если вероятность «p» события «A» в каждом испытании постоянна и отлична от 0 и 1, то вероятность «P(a, b)» того, что событие «A» появится в «n» испытаниях от «a» до «b» раз, приближенно равна определенному интегралу:

23. Математическое ожидание случайной величины и его свойства

математическое ожидание – среднее значение случайной величины.

Свойства мат. ожиданий:

1. E * const = const

2. E (cX) = c E(X)

3. E(X+Y) = EX + EY

4. E(XY) = E(X) * E(Y) (только для независимых случайных величин)

отняв мат ожидание от случайной величины - центрирование

24. Статистическое оценивание математического ожидания случайной величины

Пусть x1, x2, x3,…, x_n – это n независимых наблюдений

величины Х, тогда для оценки математического ожидания случайной величины используют статистику X:

Эта оценка является состоятельной, несмещенной и эффективной.

25. Дисперсия случайной величины и ее свойства

дисперсия – разброс значений, которые может принимать случайная величина.

Свойства дисперсии:

1. D * const =0

2. D (cX) = c² DX

3. D(X+Y) = DX + DY (только для независимых случайных величин)

стандартное отклонение – корень из дисперсии

деление на стандартное отклонение - нормирование

26. Статистическое оценивание дисперсии случайной величины

Как нам оценить дисперсию?

Да вот так:

– эта хрень называется «несмещенная оценка дисперсии»

Как бы ES² = DX. Пам. пам. пам.

27. Оценка вероятности по частоте

При проведении экспериментов часто приходится оценивать неизвестную вероятность события P по его частоте X со шрихом (нет символа ^_^) в N независимых экспериментах. Частота некоторого события в N независимых экспериментах есть не что иное, как среднее арифметическое наблюдаемых значений величины Х, которая в каждом отдельном опыте принимает значение 1 (если событие совершилось), или значение 0 (если событие не произошло):

28. Закон больших чисел

закон больших чисел – чем больше раз повторять случайный эксперимент, тем с меньшей вероятностью случайная величина отклонится от своего мат. ожидания (на нем основан статистический метод)

29. Доверительное оценивание параметров распределений

Какова точность оценки параметра? В каких границах он может лежать?

Доверительная область – это область в пространстве параметров, в которую с заданной вероятностью входит неизвестное значение оцениваемого параметра распределения. «Заданная вероятность» называется доверительной вероятностью и обычно обозначается γ (гамма)

30. Построение доверительного интервала для матожидания нормального распределения

Центрирование случайной величины – когда от нее отнимают ее мат ожидание, и получают новую случ. величину, у которой мат. ожидание = 0.

P(a < EX < b) = γ

a, b – доверительный интервал

Если задана доверительная вероятность, то a и b выглядят так:

Где – величина доверительного интервала

31. Построение доверительного интервала для дисперсии нормального распределения

Процедура деления случайной величины на ее стандартное отклонение приводит к тому, что ее DX = 1 – нормирование случайной величины

Не знаю, к чему я это вчера написал, но суть в том, что:

(D-t < D < D+t) – доверительный интервал

– формула доверительного интервала для дисперсии. S² – несмещённая оценка дисперсии; σ – среднее квадратичное отклонение

32. Статистические гипотезы. Проверка статистических гипотез

Проверки статистических гипотез — один из классов задач в математической статистике.

Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой P известно полностью или частично. Тогда любое утверждение, касающееся P, называется статистической гипотезой. 

На практике обычно требуется проверить какую-то конкретную гипотезу H₀. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза H₁, называемая конкурирующей или альтернативной.

В большинстве случаев статистические критерии основаны на случайной выборке (X1, X2, …, Xn) фиксированного объема n >= 1 из распределения P. В последовательном анализе выборка формируется в ходе самого эксперимента и потому её объем является случайной величиной .

Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза с известным уровнем значимости.