
- •Росжелдор
- •6.5 Вычисление тройного интеграла в декартовых координатах …………. 70
- •1 Неопределенный интеграл
- •1.1 Первообразная функция
- •1.2 Неопределенный интеграл
- •1.3 Основные свойства неопределенного интеграла
- •1.4 Таблица основных интегралов
- •1.5 Основные методы интегрирования
- •1.6 Интегрирование рациональных функций
- •1.7 Интегрирование выражений, содержащих тригонометрические функции
- •2.2 Основные свойства определенного интеграла
- •2.3 Производная определенного интеграла по переменному верхнему пределу
- •2.4 Формула Ньютона-Лейбница
- •2.5 Замена переменной в определенном интеграле
- •3.2 Несобственные интегралы второго рода (от неограниченных функций)
- •3.3 Признаки сходимости несобственных интегралов
- •3.4 Абсолютная и условная сходимости
- •4 Обыкновенные дифференциальные уравнения
- •4.1 Общие понятия
- •4.2 Дифференциальные уравнения первого порядка
- •4.3 Уравнение с разделяющимися переменными
- •4.5 Линейное уравнение
- •4.8 Уравнения высшего порядка, допускающие понижение порядка
- •1) Уравнение вида .
- •2) Уравнение вида .
- •3) Уравнение вида .
- •4.9 Линейные дифференциальные уравнения высшего порядка
- •4.10 Линейное однородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •1) Найти общее решение однородного дифференциального уравнения .
- •4.11 Линейное неоднородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
- •5 Системы обыкновенных дифференциальных уравнений
- •5.1 Нормальная система дифференциальных уравнений
- •5.2 Интегрирование нормальной системы методом исключения неизвестных
- •5.3 Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами
- •5.4 Понятие устойчивости решения нормальной системы по Ляпунову
- •6 Кратные интегралы
- •6.1 Двойной интеграл
- •6.2 Вычисление двойного интеграла в декартовых координатах
- •6.3 Вычисление двойного интеграла в полярных координатах
- •6.4 Тройной интеграл
- •6.5 Вычисление тройного интеграла в декартовых координатах
- •6.6 Вычисление тройного интеграла в цилиндрических и сферических координатах
- •7 Криволинейные интегралы
- •7.1 Криволинейный интеграл первого рода
- •7.2 Криволинейный интеграл второго рода
- •7.3 Связь между криволинейными интегралами первого и второго рода
- •7.4 Формула Грина
- •8 Поверхностные интегралы
- •8.1 Поверхностный интеграл первого рода
- •8.2 Поверхностный интеграл второго рода
- •8.3 Связь между поверхностными интегралами первого и второго рода
- •8.4 Формула Остроградского
- •8.5 Формула Стокса
- •9 Практические задания
- •9.1 Неопределенные интегралы
- •9.2 Обыкновенные дифференциальные уравнения первого порядка
- •9.3 Обыкновенные дифференциальные уравнения высшего порядка
8.2 Поверхностный интеграл второго рода
Пусть векторная функция
![]()
определена и
непрерывна на некоторой поверхности
![]() в пространстве
в пространстве![]()
Разобьем поверхность
![]() произвольным образом наn
частей
произвольным образом наn
частей
![]() сплощадями
сплощадями
![]()
![]() (рис. 8.3). В каждой частичной области
(рис. 8.3). В каждой частичной области![]() выберем
произвольную точку
выберем
произвольную точку
![]() и составим сумму
и составим сумму
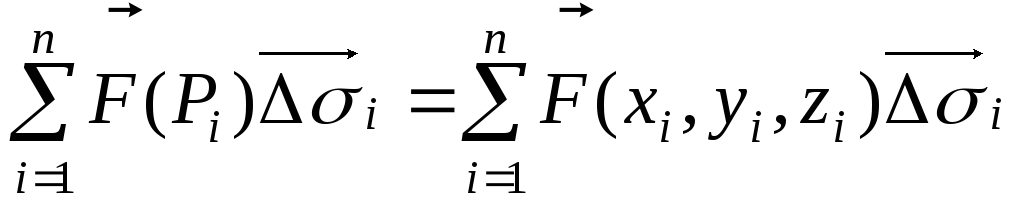 ,
,
где
![]() ,
,![]() – единичная нормаль к поверхности
– единичная нормаль к поверхности![]() в точке
в точке![]() .
.
Данная сумма
называется интегральной
суммой для
векторной функции
![]() в области (на поверхности)
в области (на поверхности)![]() .
.
Обозначим через
![]() наибольший из диаметров частичных
областей
наибольший из диаметров частичных
областей![]() :
:
![]() .
.
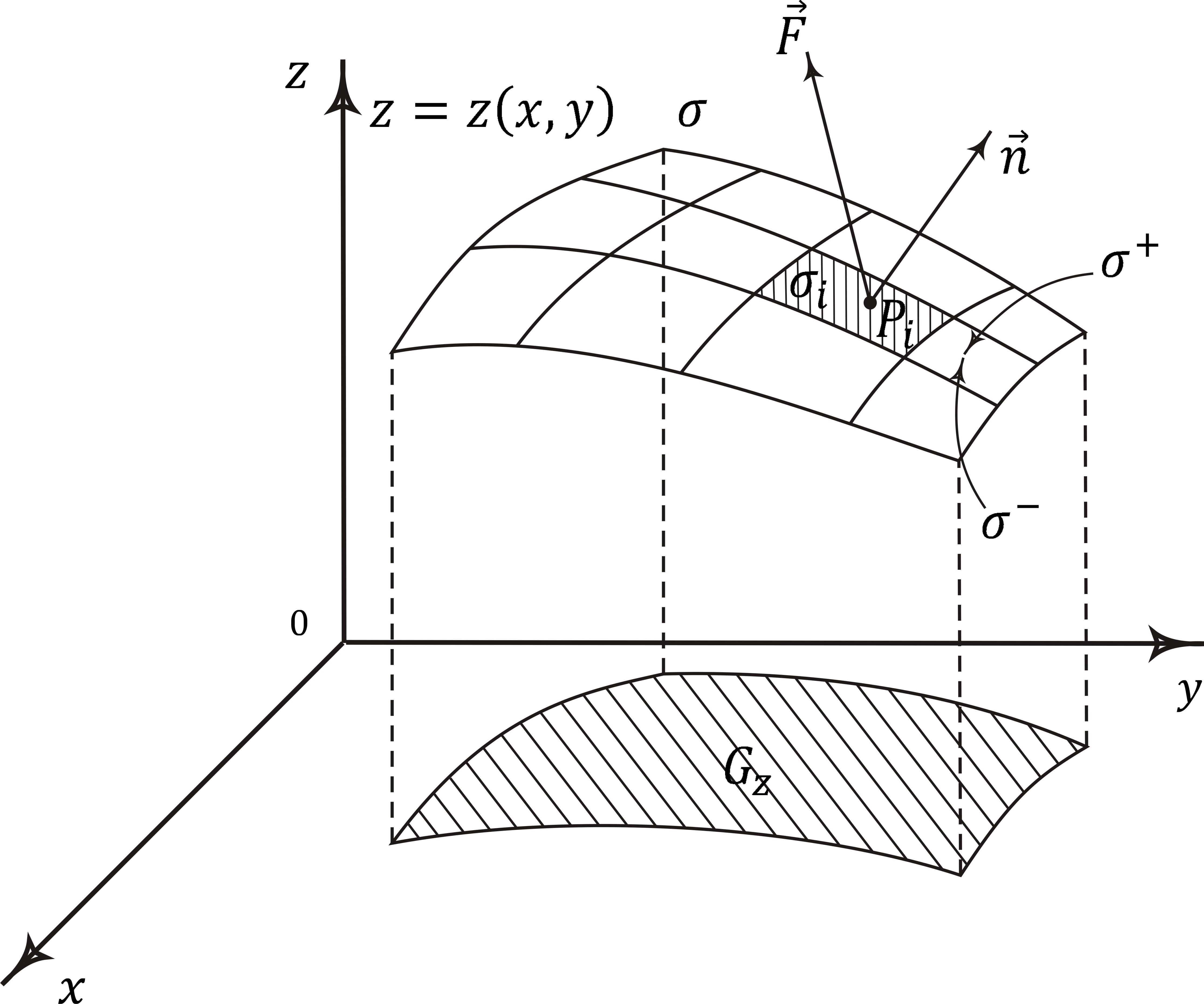
Рис. 8.3. Разбиение
поверхности
![]() на частичные области в случае
на частичные области в случае
поверхностного интеграла второго рода
Определение.
Поверхностным
интегралом второго рода от
функции
![]() по поверхности
по поверхности![]() называется предел интегральных сумм
при
называется предел интегральных сумм
при![]() ,
если этот предел существует и не зависит
ни от способа разбиения поверхности
,
если этот предел существует и не зависит
ни от способа разбиения поверхности![]() на частичные области
на частичные области![]() ,
ни от выбора в каждой из них точки
,
ни от выбора в каждой из них точки![]() :
:
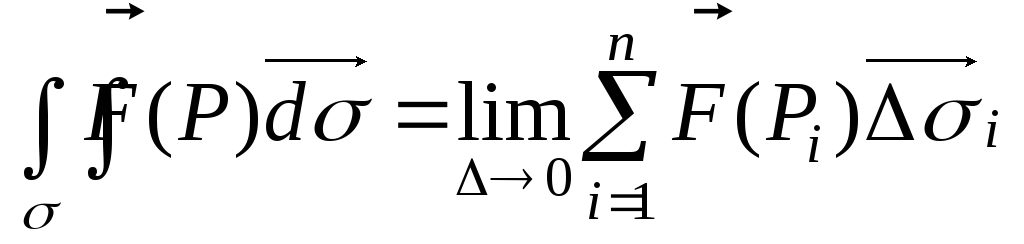
или в другой записи:
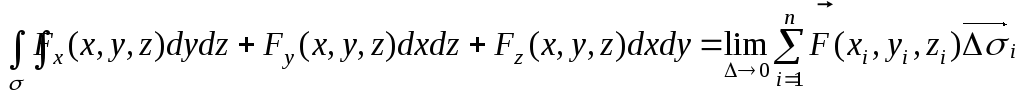 ,
,
где векторный элемент поверхности
![]()
и скалярное произведение
![]() .
.
Функция
![]()
называется
интегрируемой
по поверхности
![]() ,
сама
,
сама![]() –поверхностью
интегрирования.
–поверхностью
интегрирования.
Теорема
8.2 (существования поверхностного
интеграла второго рода) (без доказательства).
Функция
![]() ,
непрерывная на кусочно-гладкой поверхности
,
непрерывная на кусочно-гладкой поверхности![]() ,
интегрируема по этой поверхности.
,
интегрируема по этой поверхности.
Основные свойства поверхностного интеграла второго рода аналогичны соответствующим свойствам поверхностного интеграла первого рода, за исключением свойства 5:
При изменении стороны поверхности интегрирования интеграл изменяет знак (так как переход к другой стороне поверхности меняет направление нормали к поверхности на противоположное):
![]() ,
,
где
![]() и
и![]() – стороны поверхности интегрирования
– стороны поверхности интегрирования![]() .
.
Простейший
физический
смысл поверхностного интеграла второго
рода
– количество
жидкости или газа, протекающего за
единицу времени в заданном направлении
через поверхность
![]() с установившейся скоростью
с установившейся скоростью![]() .
.
Вычисление поверхностного интеграла второго рода сводится к вычислению суммы трех двойных интегралов следующим способом.
Если
![]() –
выражения, полученные из уравнения
поверхности
–
выражения, полученные из уравнения
поверхности![]() разрешением относительно соответствующих
координат;
разрешением относительно соответствующих
координат;![]() – проекции поверхности
– проекции поверхности![]() соответственно на плоскости
соответственно на плоскости
![]() ,
,![]() ,
,![]() ;
;![]() – единичная нормаль к поверхности
– единичная нормаль к поверхности
![]() в точке
в точке![]() (рис. 8.3), то
(рис. 8.3), то
![]()
![]() ,
,
где знаки у двойных
интегралов соответствуют знакам
направляющих косинусов
![]() нормали
нормали![]() к поверхности
к поверхности![]() .
.
Пример. Вычислить поверхностный интеграл второго рода
![]() ,
,
где
![]() – верхняя сторона плоскости
– верхняя сторона плоскости![]() ,
отсеченная плоскостями
,
отсеченная плоскостями![]() и лежащая в первом октанте (рис. 8.4).
и лежащая в первом октанте (рис. 8.4).
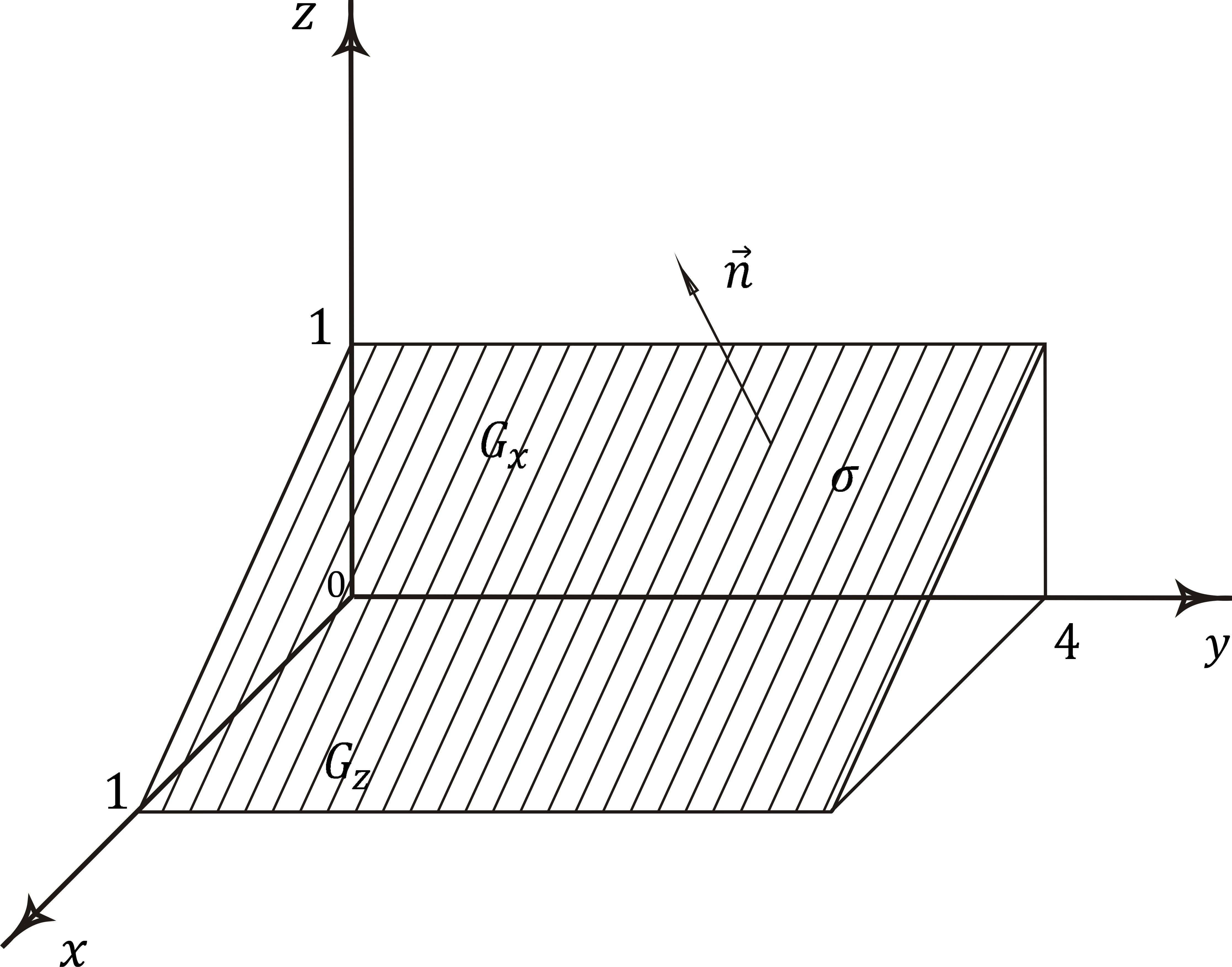
Рис. 8.4. Пример вычисления поверхностного интеграла второго рода
Обозначим через
![]() – проекции поверхности
– проекции поверхности![]() на плоскости
на плоскости
![]() ,
,![]() ,
,![]() соответственно.
Как видно из рис. 8.4, направляющие косинусы
нормали
соответственно.
Как видно из рис. 8.4, направляющие косинусы
нормали
![]() к поверхности
к поверхности![]()
![]() ,
а
,
а![]() ,
так как плоскость
,
так как плоскость![]() параллельна осиOy.
Следовательно, по формуле вычисления
поверхностного интеграла второго рода
получим:
параллельна осиOy.
Следовательно, по формуле вычисления
поверхностного интеграла второго рода
получим:
![]()
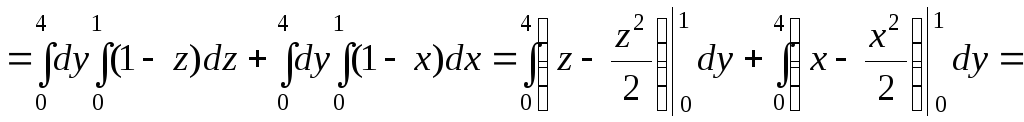
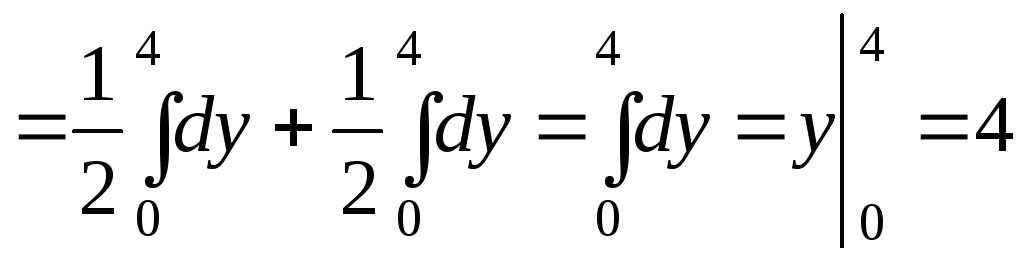 .
.
8.3 Связь между поверхностными интегралами первого и второго рода
Используя выражение для скалярного произведения двух векторов
![]() ,
,
![]()
через их координаты
![]() ,
,
получим формулу, выражающую поверхностный интеграл второго рода через поверхностный интеграл первого рода и устанавливающую связь между этими интегралами:
![]()
![]() .
.
