5.3 Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами

Определение. Нормальной системой линейных дифференциальных уравнений с постоянными коэффициентами называется нормальная система вида

где коэффициенты – заданные действительные числа.

Нормальную систему линейных дифференциальных уравнений с постоянными коэффициентами удобно записывать в векторно-матричной форме

,

где

, .

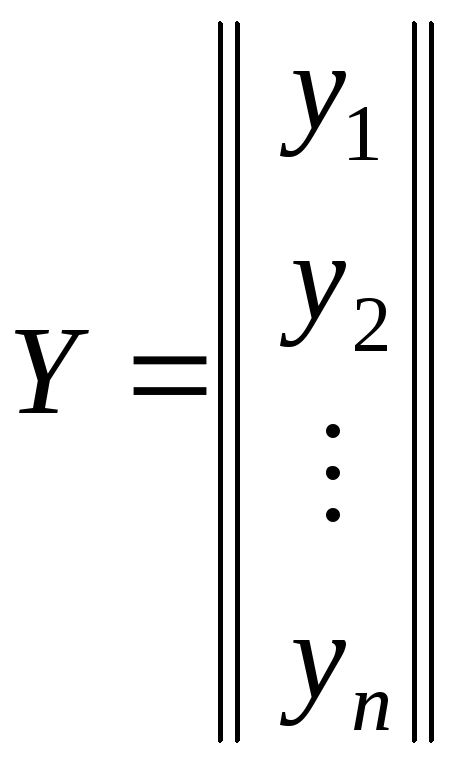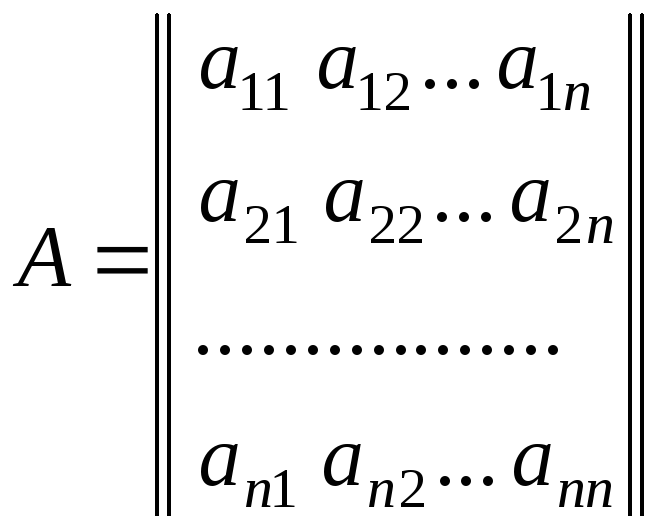Для рассматриваемой нормальной системы имеет место теорема о структуре общего решения, аналогичная теореме 4.3 для линейного однородного дифференциального уравнения высшего порядка с постоянными коэффициентами. Именно, общим решением нормальной системы линейных дифференциальных уравнений с постоянными коэффициентами является линейная комбинация

n линейно независимых частных решений этой системы

, , … ,.

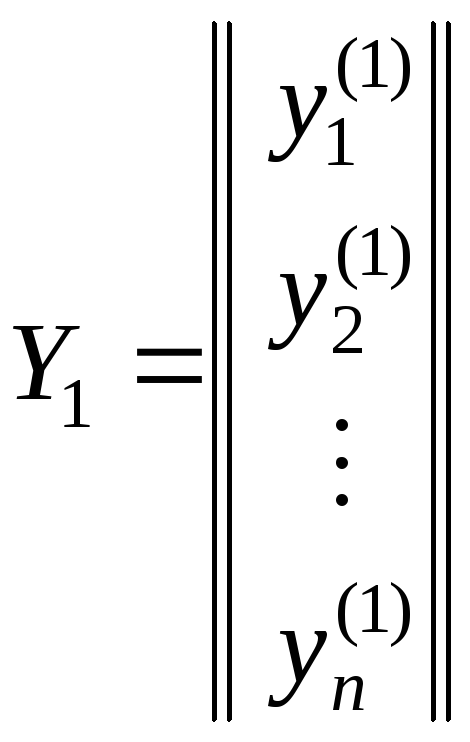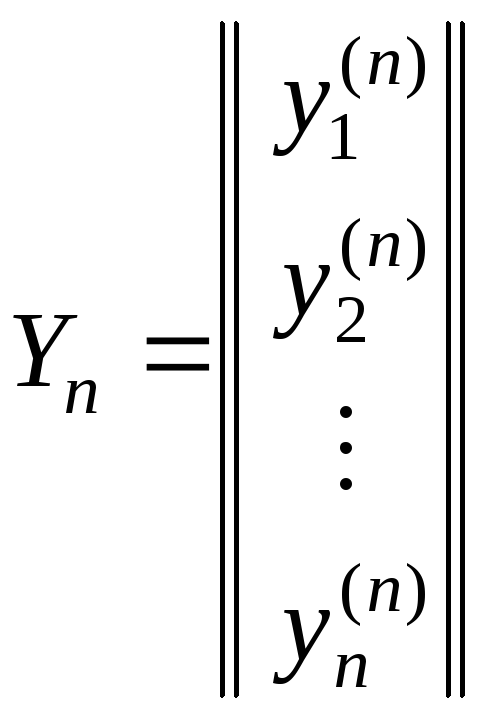Для их нахождения составляется и решается характеристическое уравнение

,

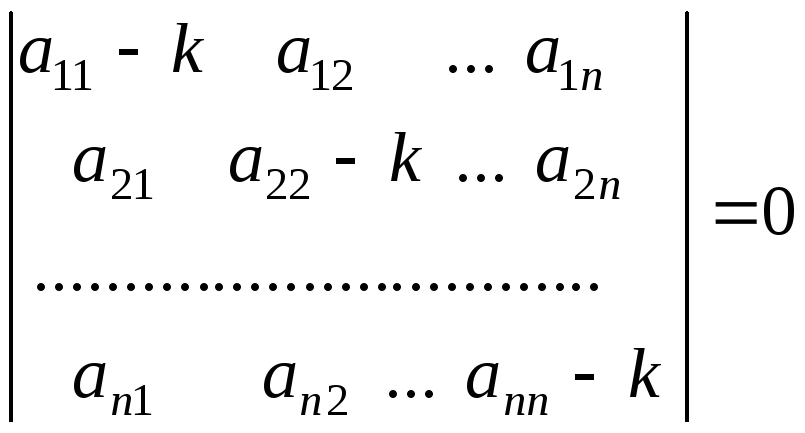представляющее собой алгебраическое уравнение n-ой степени относительно k.

Ограничимся случаем, когда характеристическое уравнение имеет различные (простые) действительные корни . Тогда каждому изn корней характеристического уравнения соответствует одно изn линейно независимых частных решений вида

,

причем элементы матрицы

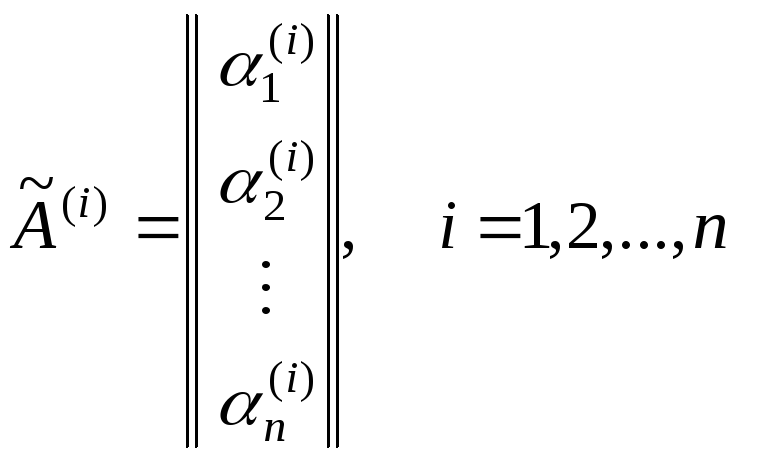
находятся из системы уравнений

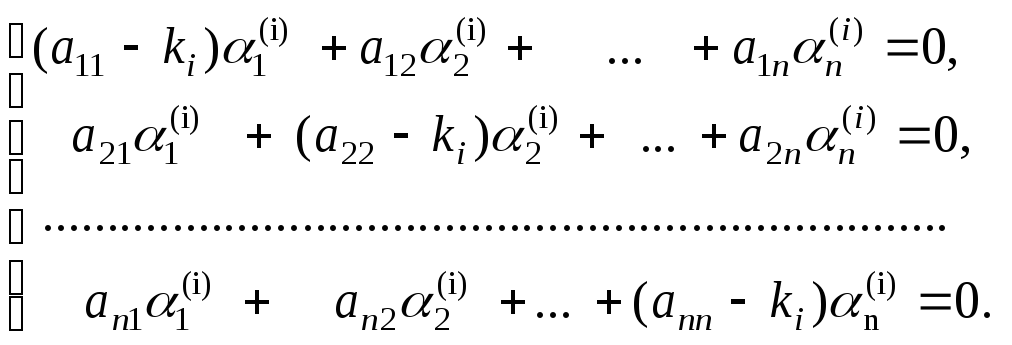
Следует заметить, что элементы определяются из этой системы для каждогонеоднозначно, так как определитель системы равен нулю (см. характеристическое уравнение) и, следовательно, по крайней мере одно уравнение является следствием остальных. Неоднозначность определениясвязана с тем, что решение нормальной системы линейных дифференциальных уравнений с постоянными коэффициентами остается решением той же системы при умножении на произвольный постоянный множитель.

Взяв линейную комбинацию найденных линейно независимых частных решений

,

получаем общее решение нормальной системы

или в векторно-матричной форме

.

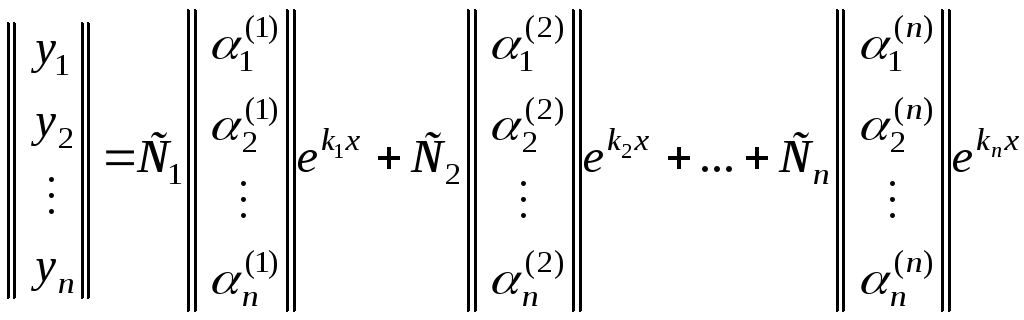Пример. Найти общее решение системы

Составим и решим характеристическое уравнение

.

Частные решения нормальной системы, соответствующие найденным корням, имеют вид

;

.

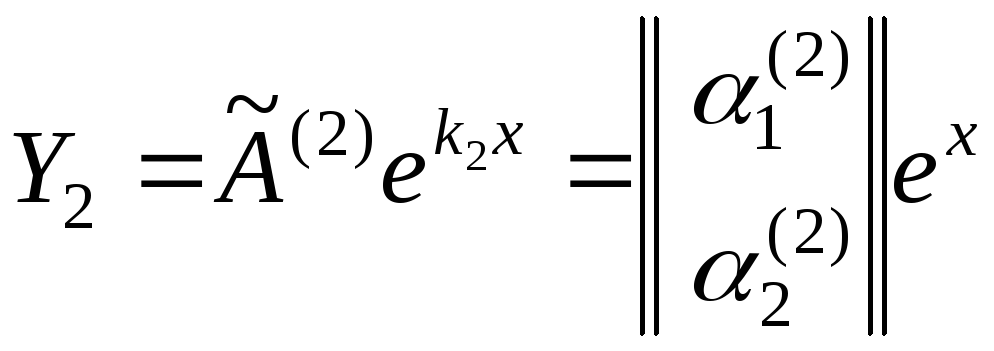Система уравнений для определения элементов матрицы призапишется таким образом:

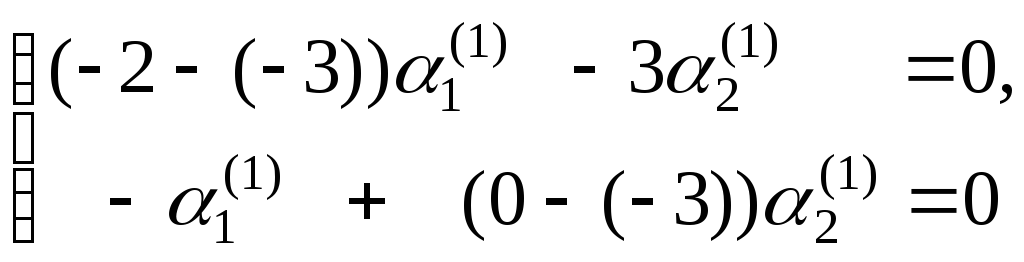или

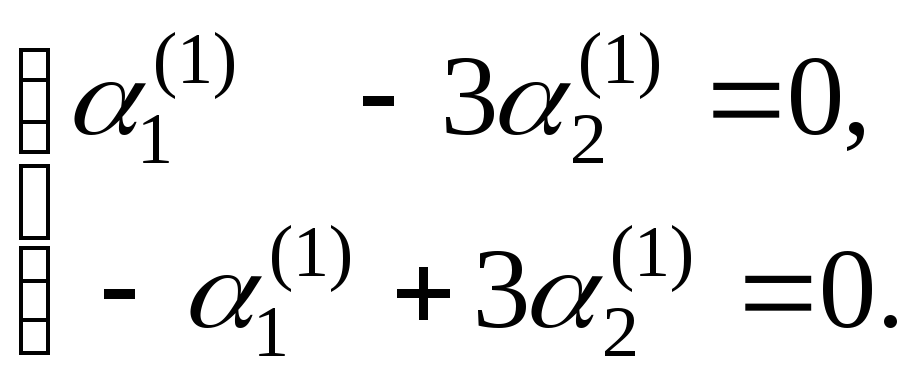
Эта система имеет бесчисленное множество решений, так как второе уравнение есть следствие первого. Полагая, например, , находим.

Итак, корню характеристического уравнения соответствует частное решение

.

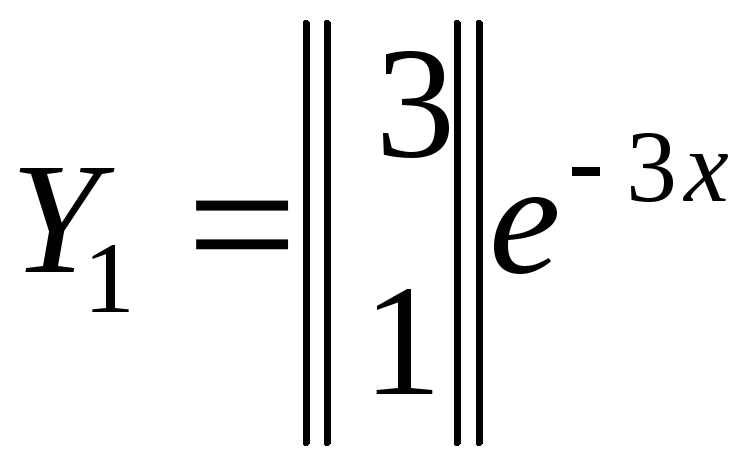Система уравнений для определения элементов матрицы призапишется таким образом:

или

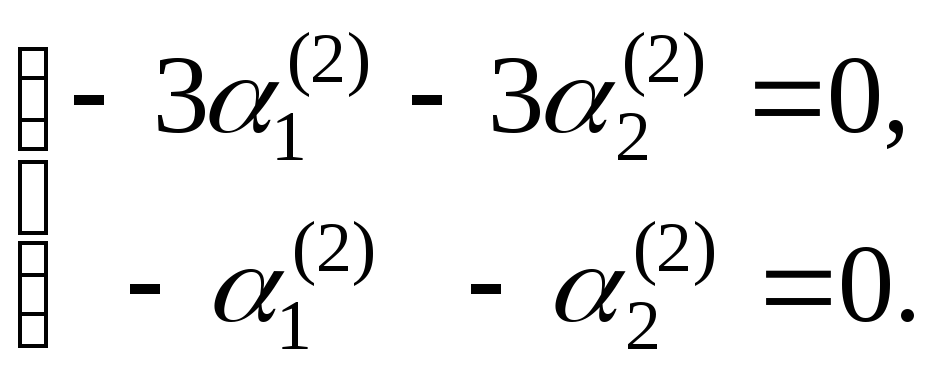
Эта система имеет бесчисленное множество решений, так как второе уравнение есть следствие первого. Полагая, например, , находим.

Итак, корню характеристического уравнения соответствует частное решение

.

Общее решение исходной нормальной системы имеет вид

или

.

5.4 Понятие устойчивости решения нормальной системы по Ляпунову

Рассмотрим нормальную систему дифференциальных уравнений

с начальными условиями в точке .

Определение. Решение нормальной системы называетсяустойчивым по Ляпунову, если для любого найдется такое, что для любого решениятой же системы, начальные значения которого в точкеудовлетворяют неравенствам

,

для всех справедливы неравенства

.

Если решение устойчиво по Ляпунову и, кроме того,

,

то оно называется асимптотически устойчивым.

Замечание. Исследование на устойчивость решения нормальной системы может быть сведено к исследованию на устойчивость тривиального нулевого решения –точки покоя некоторой нормальной системы, аналогичной исходной нормальной системе.

Можно доказать, что точка покоя заведомо устойчива по Ляпунову (асимптотически устойчива) для нормальной системы линейных дифференциальных уравнений с постоянными коэффициентами

,

если все корни характеристического уравнения системы имеют отрицательные действительные части.

Пример. Исследовать на устойчивость точку покоя системы

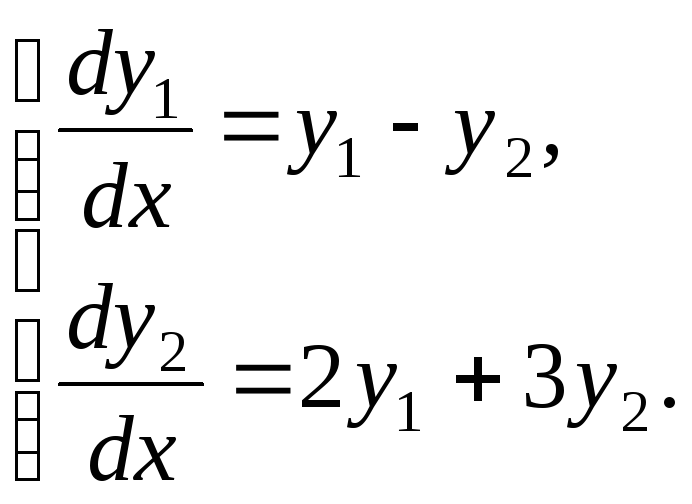
Характеристическое уравнение системы

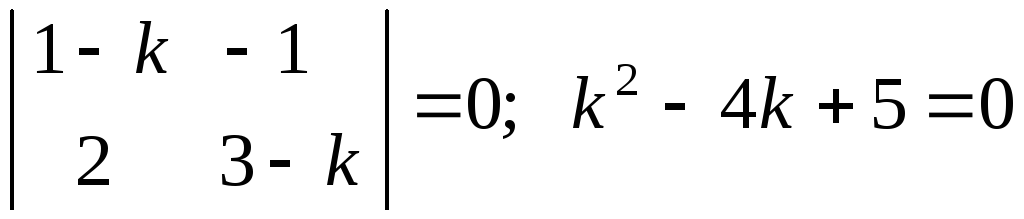
имеет пару комплексно сопряженных простых корней .

Действительная часть этих корней положительна (равна двум), поэтому точка покоя является неустойчивой.