Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный горный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

BIS5_matem_org_ua

.pdf

Скачиваний:

Добавлен:

06.06.2015

Размер:

1.77 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

(53)2 =1 +( ba )2 ( ba )2 = 95 −1 = 169 ba = 34 .

Тогда уравнения асимптот в декартовых координатах будет

y = ± 4 (x +5) 4x −3y + 20 = 0 и 4x +3y + 20 = 0 .

Подставляя

в эти

уравнения

x = ρcosϕ,

y = ρsinϕ

разрешая

их

относительно ρ , находим полярные уравнения асимптот:

ρ =

−20

3sinϕ −4cosϕ

4cosϕ +

3sinϕ

3. ПЛОСКОСТЬ

Всякое уравнение первой степени

Ax + By +Cz + D = 0 ,

ти

(49)

A, B,C

те

где

одновременно

не

нулю,

определяет

плоскость.

равны

плоскости. Вектор N = ( A; B;C)

Уравнение (49) называется общим уравнением.org

matem

называется нормальным вектором плоскости.

Уравнение

плоскости, шпроходящей через

точку

; y

; z

)

= ( A; B;C) имеет вид

перпендикулярной векторувN

− x0 ) + B( y − y0 ) +C(z − z0 ) = 0 .

(50)

рA(x

в отрезках

Уравнение плоскостие

=1,

(51)

где

a,b,c –

длины отрезков, отсекаемых плоскостью на координатных

осях, взятые с соответствующими знаками.

Уравнение плоскости, проходящей через три данные точки M1(x1; y1; z1) , M2 (x2; y2; z2 ) и M3 (x3; y3; z3 ) , имеет вид

	x − x1	y − y1	z − z1

	x2 − x1	y2 − y1	z2 − z1	= 0 .	(52)
	x3 − x1 y3 − y1		z3 − z1
Нормальным уравнением плоскости называется уравнение вида
	xcosα + y cos β + z cosγ − p = 0 ,				(53)
где cosα,cos β,cosγ		– направляющие косинусы			перпендикуляра,

проведенного из начала координат к данной плоскости, а p – его длина.

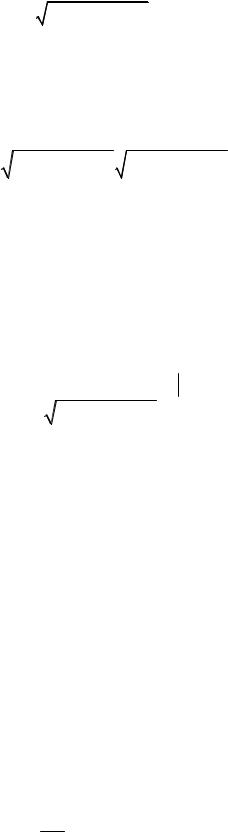
Для приведения общего уравнения плоскости (49) к нормальному виду (53) следует умножить все его члены на нормирующий множитель

µ = ±

(54)

A2 + B2 +C2

знак которого выбирается противоположным знаку свободного члена D в

общем уравнении плоскости.

A1x + B1 y +C1z + D1 = 0

Угол

между

плоскостями

A2 x + B2 y +C2 z + D2 = 0 определяется по формуле

cosϕ =

A1A2 + B1B2 +C1C2

(55)

A2 + B2

+C2

+ B2

+C2

Условие параллельности двух плоскостей имеет вид:

(56)

Условие перпендикулярности двух плоскостей имеет вид:

A1A2 + B1B2 +C1C2 =

0 .

(57)

Расстояние

от точки

0 (x0 ; y0 ; z0 )

плоскости

Ax + By +Cz + D = 0

до

находится по формуле

ти

Ax + By

+Cz

+ D

те

d =

.org2

(58)

+мB

matem

Задача 83. Составить уравнение плоскости, перпендикулярной оси Ox и

−1;−6) .

проходящей через точку K (4;

Решение.

Плоскость,

перпендикулярная

оси

Ox , параллельна

координатной плоскости yOz и ее уравнение имеет вид Ax + D = 0 . Подставляя

в это уравнение координаты точки K , получим 4 A + D = 0 , т.е. D = −4A. Следовательно, уравнение плоскости Ax −4 A = 0 или x − 4 = 0 .

Задача 84. Составить уравнение плоскости, проходящей через ось Oz и

точку L(5;−2;7) .

Решение. Так как плоскость проходит через ось Oz , то ее уравнение имеет вид Ax + By = 0 . Подставляя в это уравнение координаты точки L ,

получим 5A −2B = 0 или A = 25B . Таким образом, имеем 2Bx5 + By = 0 .

Откуда получаем 2x +5y = 0 .

Задача 85. Составить уравнение плоскости, параллельной оси Ox и проходящей через точки M (1;−1;−3) и N (−5;4;−2) .

Решение. Поскольку плоскость параллельна оси Ox , ее уравнение имеет вид By +Cz + D = 0 . Подставляя в это уравнение координаты точек M и N , имеем систему двух уравнений с тремя неизвестными:

−B −3C + D = 0,

или

B +3C = D,

+4B − 2C + D = 0,

4B + 2C = D.

Откуда

B = −

C =

. Следовательно,

искомое

уравнение

записывается в виде

−

+ D = 0

или

y −5z −Г14 = 0 .

Задача 86. Даны точки M1(−3;7;−5)

(−8;3;−4) . Составить уравнение

плоскости, проходящей через точку M

ти

и перпендикулярной вектору M M

те

org

Решение.

Имеем

Найдем координаты нормального вектора N = M M

matem

N = (−8 −(−3);3 −7;−4 −(−5)) =

(−5;

−4;1) .

Подставляя

значения

точки

уравнение

вектора

A(x − x ) + B( y − y ) +C(z −ыz ) = 0 , получим искомое уравнение

−5(x +3) −

или 5x + 4 y − z −18 = 0 .

4( y −д7)

+(z +5) = 0

Задача 87. Построить плоскость 3x −12 y −8z + 6 = 0 .

Решение. Запишем уравнение плоскости в отрезках:

3x −12 y −8z = −6

−

12 y

−

=1 или

=1.

−6

−2

Плоскость пересекает ось Ox в точке x = −2 ; ось Oy – в точке y =

; ось

Oz – в точке z =

. Строим плоскость (рис. 33).

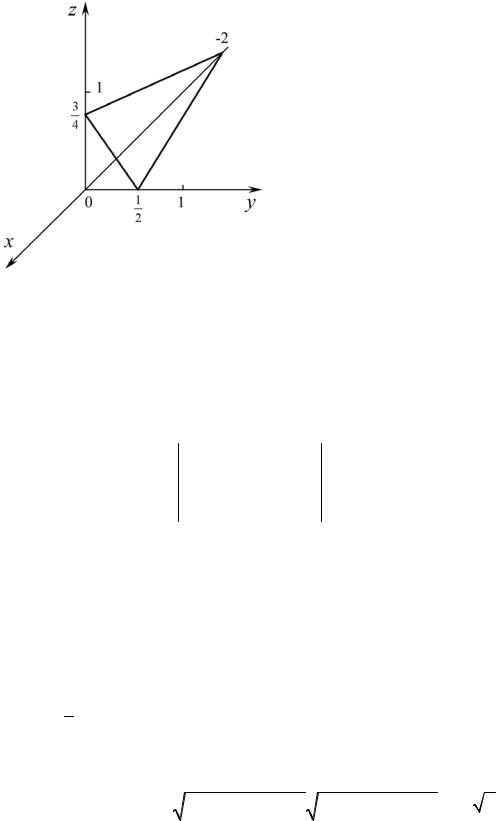
Указание. Эти же значения x, y, z

можно получить, придавая поочередно любым двум из переменных значения равные нулю:

y = 0, z = 0, 3x = −6 x = −2;
x = 0,	z = 0, −12 y = −6 y =	1	;
		2
x = 0,	y = 0, −8z = −6 z = 3 .
	4

Рис. 33

через три точки:

Задача 88. Составить уравнение плоскости, проходящей"Н

M1(1; −3;4) , M2 (0;−2;−1) и M3

(1;1;−1) .

через данные три точки,

Решение. Уравнение плоскости, проходящейи

имеет вид (52):

ти

те

x −1

y +3

z −4

org

−1

= 0 .

−5

15(x −1) −5( y +3)

− 4(ыz − 4) =matem0

или 15x −5y − 4z −14 = 0 .

−5

по элементам первой строки, получаем

Раскладывая этот определительш

Задача 89. Найти острый угол между плоскостями 7x −11y +8z +19 = 0 и

x + 4 y −10z −5 =К0 .

Решение. Первая плоскость имеет

1 = (7;−11;8) ;

нормальный вектор N

вторая – N2 = (1;4;−10) .

Угол ϕ между плоскостями равен углу между нормальными векторами.

cosϕ =

1N2

7 1 +(−11) 4 +8 (−10)

= −

72 +(−11)2 +82 12 +42 +(−10)2

Отсюда ϕ = 3π

. Острый угол между плоскостями α =π −

3π

π .

Замечание. Острый угол можно найти, пользуясь формулой cosϕ =

1N2

, так как

косинус такого угла положительный.

Задача 90. Составить уравнение плоскости, проходящей через точку M (−4;3;−7) параллельно плоскости 6x −5y + 4z −15 = 0 .


Решение. Так		как	искомая	плоскость параллельна		плоскости
6x −5y + 4z −15 = 0 , то в			качестве ее	нормального	вектора можно взять
нормальный вектор		= (6;−5;4) данной плоскости.			Используя	уравнение
	N
						, получим
плоскости, проходящей через точку M перпендикулярно вектору N
6(x + 4) −5( y −3) + 4(z +7) = 0				или 6x −5y + 4z + 67 = 0 .

Задача 91. Составить уравнение плоскости, проходящей через точки A(1;4;−5) и B(4;2;−3) и перпендикулярной плоскости 3x +5 y −6z −8 = 0 .

Решение. В качестве нормального вектора N искомой плоскости можно

взять вектор, перпендикулярный вектору

AB = (3;−2;2)

и нормальному вектору

1 = (3;5;−6) данной плоскости. Так как векторное произведениеЗ

двух векторов

есть вектор,

перпендикулярный

, то

за N можно

векторам-сомножителямВ

принять векторное произведение

AB и N1

, т.ке.

ти

те

N = AB ×N

-2

org

+24 j

+ 21k = (2;24;21) .

3 5м -6

matem

Используем далее уравнение плоскости, проходящей через данную точку

A(1;4;−5) перпендикулярно вектору N = (2;24;21) :

2(x −

+ 21(z +5) = 0

или

2x +24 y +21z +7 = 0 .

1) + 24( y − 4)

плоскости, проходящей через точку

Задача 92. Написать уравнение

M (−1;−1;2)

перпендикулярной

плоскостям

x − 2 y + z − 4 = 0

x + 2 y − 2z + 4 = 0 .

Решение. В качестве нормального вектора N искомой плоскости возьмем векторное произведение нормальных векторов N1 = (1;−2;1) и

N2 = (1;2;−2) данных плоскостей: i j k

N = N1 ×N2 = 1 -2 1 = 2i +3 j +4k = (2;3;4) . 1 2 -2

Далее остается воспользоваться уравнением плоскости, проходящей через данную точку M (−1;−1;2) перпендикулярно вектору N = (2;3;4) :

2(x +1) +3( y +1) + 4(z − 2) = 0 или 2x +3y + 4z −3 = 0 .

Задача 93.	Написать уравнение плоскостей, параллельных плоскости
x − 2 y + 2z −7 = 0	и отстоящих от нее на расстоянии, равном 5.

Решение. Запишем уравнение искомой плоскости в виде x − 2 y + 2z + D = 0 .

Найдем расстояние между плоскостями, для этого возьмем произвольную точку данной плоскости и определим ее расстояние до искомой плоскости.

Полагая x = 0, y = 0 , найдем z =

7 , т.е. получаем точку M (0;0; 7 ) .

Расстояние от точки M до плоскости x − 2 y + 2z + D = 0

Ax0 + By0 +Cz0 + D

1 0 + 2 0 + 2 7

+ D

d =

+ B

+ (−2)

+ 2

Так как по условию d =5 , то для определенияЗD получаем уравнение

7 + D

или

7 + D

=15 ,

или 7 + D

= ±15 .

Откуда D1 =8,

org

D в уравнение искомой

D2 = −22 . Подставляя значения

matem

плоскости, получаем уравнения двух плоскостей

= 0

x −2 y + 2z − 22 = 0 .

x − 2 y + 2zс+8

Задача 94.

6x −3y − 2z +35 = 0 привести к

еУравнение плоскости

нормальному видуа.

Решение. Находим нормирующий множитель (54)

µ = ±

= −

1 .

62 +32 + 22

Здесь берется знак минус, так как D =35 > 0 .

Умножив уравнение плоскости на (−

1 ) , получим нормальное уравнение

заданной плоскости

−

6 x +

3 y +

2 z −5 = 0 .

4. ПРЯМАЯ В ПРОСТРАНСТВЕ
Уравнения прямой, проходящей через точку M0 (x0 , y0 , z0 ) и параллельно
вектору a = (l, m, n) , записываются в виде
x − x0	= y − y0	= z − z0 .	(59)
l	m	n

Уравнения (59) называются каноническими уравнениями прямой, а вектор a – направляющим вектором прямой.

Если каждое из отношений (59) приравнять параметру t , то получаются

параметрические уравнения прямой

= x0 +lt,

= y0 + mt,

(60)

= z0 + nt.

Уравнения прямой,

проходящей

через

M (x , y , z ) и

две точки

1 1 1 1

M2 (x2 , y2 , z2 ) имеют вид

x − x

y − y

z − z

. В

(61)

x2 − x1

y2 − y1

− z1

те

ти

Угол между прямыми

2.org

z − z

x − x

y − y

z − z

xа− x

y − y

matem

определяется по формулеы

l1l2 + m1m2 + n2n2

cosеϕ =

(62)

l1 + m1 + n1 l2 + m2 + n2

Условие параллельности двух прямых имеет вид:

l1 = m1 = n1 . l2 m2 n2

Условие перпендикулярности двух прямых имеет вид:

l1l2 + m1m2 + n2n2 = 0 .

Угол между прямой

x −l x0 = y −my0 = z −nz0

и плоскостью

Ax + By +Cz + D = 0

(63)

(64)

(65)

(66)

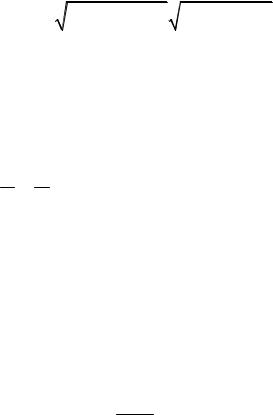
определяется по формуле

	Al + Bm +Cn
sinϕ =		.
	A2 + B2 +C2 l2 + m2 + n2

Условие параллельности прямой (65) и плоскости (66) имеет вид:

Al + Bm +Cn = 0 .

Условие перпендикулярности прямой и плоскости имеет вид:

Al = mB = Cn .

(67)

(68)

(69)

Задача 95. Составить канонические уравнения прямой, проходящей через

точку A(−5;8;−3) и параллельной вектору s =

(2;4;−1) .

Решение.

Воспользуемся

(59)

при

формулойУ

x0 = −5, y0 =8, z0 = −3, l = 2, m = 4, n = −1:

x +5

y −8

z +

ти

3а

–

те

−1

org

matem

прямой.

это и есть канонические уравненияй

Задача 96. Составить параметрические уравнения прямой, проходящей

через точку A(−7;−3;2)р, перпендикулярной плоскости x − 4 y −5z +8 −0 . Найти

точку

M прямой, соответствующую значению параметра t = 2 .

Решение. Так как нормальный вектор

N = (1;−4;−5)

данной плоскости

перпендикулярен ей, то по условию он должен быть параллелен искомой прямой. По формулам (60), где x0 = −7, y0 = −3, z0 = 2, l =1, m = −4, n = −5 ,

получаем параметрические уравнения прямой:

x = −7 +t,y = −3 − 4t,z = 2 −5t.

При t = 2 находим x = −5, y = −11, z = −8 , т.е. получим точку

M (−5;−11;−8) .

Задача 97. Написать уравнения прямой l , проходящей через точки

A(−1;2;3) и B(5;−2;1) . Лежат ли на этой прямой точки K(−7;6;5) , L(2;0;1) ?

Решение.

Используя

формулу

(61),

при

x1 = −1,

y1 = 2,

z1 =3, x2 =5,

y2 =−2, z2 =1 получим искомые канонические уравнения прямой l :

x +1

y − 2

z −3

−4

−2

L , соответственно

Подставляя в эти уравнения координаты точек

находим

−7 +1 =

6 −2

5 −3

2 +1

0 − 2 ≠ 1 −3 .

= −1,

−4

−2

−4

Следовательно,

K l , а L l .

Задача

98.

Найти

канонические

по

которой

уравнения прямой,

пересекаются плоскости x − 2 y

+3z +15 = 0 и 2x

− 4z −12 = 0 .

Решение. Направляющий

прямой

должен быть

вектор искомой

ти

N1 = (1;−2;3) и

перпендикулярен нормальным векторам заданных плоскостей

N2 = (2;3;−4) . В

качестве

вектора

взять

векторное

произведение

ожно

векторов N1 и N2 :

те

org

matem

a = N1 ×N2 =

= −i

+10j

+7k

или a = (−1;10;7) .

1 −

ы2

−4

Очевидно,

что

самой

прямой

определяется системой

уравнение

уравнений

x −

2 y +3z +15 = 0,

2x +3y − 4z −12 = 0.

Для нахождения точки M0 (x0 , y0 , z0 )

прямой положим, например, z0 = 0 .

Тогда из системы

x −2 y +15

= 0,

получаем

x0 = −3,

y0 = 6 .

2x +3y −12 = 0.

Итак, искомая точка прямой M0 (−3,6,0) .

По точке M0 и вектору a составляем канонические уравнения прямой по

формуле (59):

x−+13 = y10−6 = 7z .

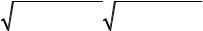
Задача 99. Найти угол ϕ между прямыми

x −1

y +5

z −7

x −4

y +5

z −6

−2

−3

−2

Решение. По формуле (62) получаем

cosϕ =

−2 1 + 6 2 +(−3) (−2)

= 16 .

22 + 62 +32 12 + 22 + 22

≈ 40D,37 .

Отсюда ϕ = arccos

Задача 100. Составить уравнения

прямой,

проходящей

через точку

A(−3;8;−9) и параллельной прямой

x = 4 −5t,

y = 2t,

= −7

+10t.

ти

Решение. Запишем уравнение данной прямой в каноническом виде

x − 4

аy

=м

те

−5

Так как

искомая

прямая

данной,

то

качестве

ее

параллельна.org

направляющего

вектора

matem

a = (−5;2;10)

можнойвзять направляющий вектор

данной прямой.

Используя теперь уравненияы

прямой (59), проходящей через точку

A и

параллельно вектору a

,аполучаем

y −

z +9

−5

Задача 101. Составить уравнения

прямой, проходящей через точку

M (−7,0,9) перпендикулярно двум данным прямым

x −3

y + 4

z −5

x +1

y −3

z −2

−2

−1

−5

Решение. Найдем направляющий вектор a

искомой прямой. Так как он

должен быть

перпендикулярен

направляющим

векторам

заданных прямых

a1 = (−2;−1;3)

a2 = (4;6;−5) ,

то вместо

него

можно

взять векторное

произведение векторов a1 и a2 :

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.2016924.3 Кб237Bezopas_dvizhenia_rus_2.docx
#
18.09.201934.95 Кб1Bilet_vse_25.docx
#
24.04.20195.11 Mб2Bilyavskiy.doc
#
06.06.20151.34 Mб9BIS3_matem_org_ua.pdf
#
06.06.20151.4 Mб12BIS4_matem_org_ua.pdf
#
06.06.20151.77 Mб16BIS5_matem_org_ua.pdf
#
28.03.20162.42 Mб8book_full.pdf
#
15.11.2019564.21 Кб1Brif_dlya_konsultantov_ISTINNAYa_iyul_2012.docx
#
26.08.2019102.02 Кб2bukhuchet.docx
#
22.11.2019185.21 Кб2BYuDZhETUVANNYa_Rob_zoshit_dlya_studentiv.docx
#
06.06.2015755.71 Кб33ch5 в работе.doc