Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный горный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

BIS5_matem_org_ua

.pdf

Скачиваний:

Добавлен:

06.06.2015

Размер:

1.77 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Задача 29. Составить уравнение окружности в каждом из следующих случаев:

1)центр окружности совпадает с началом координат и ее радиус r = 7 ;

2)центр окружности совпадает с точкой С(2;–3) и ее радиус r = 7 ;

3)окружность проходит через начало координат и ее центр совпадает с точкой С(6;–8);

4)окружность проходит через точку А(2;6) и ее центр совпадает с точкой

С(–1;2);

5)точки А(3;–2) и В(–1;6) являются концами одного из диаметров окружности.

Решение:

1) используя каноническое уравнение окружности (15), находим x2 + y2 = 49 ;

используя нормальное уравнение окружности (14),"составляем

(x −2)

+( y +3)

= 49 ;

находим сначала радиус

r окружности как длину радиус-вектора

точки С по формуле

x2 + y2 ,

r =

62 + (−8)2 =

100ти=10 .

те

уравнение окружности

Затем, используя формулу (14), составляемм .ua

(x −6)2 +( y +8)2 =100

org

;

matem

окружности по формуле

аналогично предыдущемуй, находим радиус r

r =

)2 +

( y − y

;

(xш− x

сC

+ (2 −6) = 25 = 5 .

r = (−1 − 2)

Затем составляемдуравнение окружности

+1)2 +( y −2)2

= 25 ;

C( xC , yC ) есть середина отрезка АВ, координаты

центр окружности

середины отрезка находим по формулам:

x =

xA + xB

;

y =

yA + yB

;

x =

3 +(−1)

=1;

y = −2 +6 =

= 2 .

Расстояние АВ – диаметр 2r окружности, поэтому

(2r)2 = AB 2 = (−1 −3)2 +(6 +2)2 =80 .

Отсюда r2 = 804 = 20 .

Используя нормальное уравнение (14), получим искомое уравнение окружности

(x −1)2 +( y −2)2 = 20 .

Задача 30. Составить уравнение окружности, которая касается осей координат и проходит через точку А(–2;1).

Решение. Поскольку точка А(–2;1) находится во втором квадрате и окружность, проходящая через нее, касается осей координат, то она полностью расположена во втором квадрате. Следовательно, абсцисса x0 ее центра

отрицательна, а ордината положительна.

Поэтому x0 =−r, y0 =r (r >0) . Внеся эти значения в нормальное уравнение окружности,

имеем:

(x + r)2 +( y −r)2 = r2 .

Значение

"r определим исходя

O``

из условия, чтоГокружность проходит

через точку"А(–2;1) и ее координаты

удовлетворяют

написанному

уравнениюВ .

Замена

текущих

координати

х, у данными –2 и 1

приводитти

к уравнению:

-5

-2

.ua

(−2 + r)

+(1 −r)

= r

те

org

или

matem

−6r +5 = 0 r1 =1,

r2 =5

Рис. 13

(по

теореме Виета:

r1 + r2 = 6, ).

r1 r2 = 5

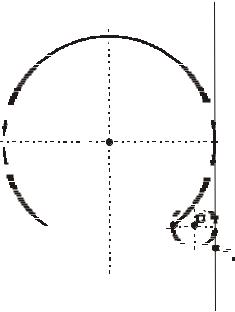
Следовательно, возможны две окружности, проходящие через точку

осей координат. У первой из них

А(–2;1) и касающиесяК

x0 = −1, y0 =1, r =1;

У второй –

x0 = −5, y0 =5, r =5 .

Уравнение первой окружности –

(x +1)2 +( y −1)2 =1 или x2 + y2 + 2x −2 y +1 = 0 .

Уравнение второй –

(x +5)2 +( y −5)2 = 25 или x2 + y2 +10x −10 y + 25 = 0 (рис. 13).

Задача 31. Найти координаты центра и радиус окружности 3x2 +3y2 −4x +6 y −12 = 0 . Построить окружность.

Рис. 14

ти

Решение. Приведем данное уравнмние.кuaнормальному виду

org

matem

(x − x0 )

+( y − y0 )

= r

Для этого разделим данноеш

уравнение на коэффициент 3 (при x2 и

−

+ 2 y −

+ y

4 =

0 .

содержащие x , в одну группу,

а содержащие

Соединим чл ны,

другую, получим:

2 − 4 x) + ( y2 + 2 y) = 4

или (x

2 −2

2 x) + ( y2

+ 2 1y) = 4 .

y2 ):

y , – в

Дополним первый и второй квадратный двучлен до полного квадрата соответственно разности и суммы двух чисел. Для этого прибавим к первому

двучлену 94 = ( 32)2 , ко второму 1 =12 , а чтобы знак равенства в уравнении сохранился, прибавим 94 и 1 также и к правой части уравнения. Имеем:

(x	2	−2x	2	+	4	) +( y	2	+2 y 1	+1)	= 4 +	4	+1 или (x −	2	)	2	+( y +1)	2	=	49	.
			3		9						9		3						9

Сравнивая это уравнение с нормальным уравнением окружности,

заключаем, что
x = 2		, y = −1, r = 7		= 2 1 .
0	3	0	3		3
	3		3		3	2
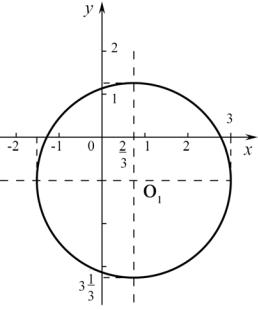
Далее		в системе координат ОХУ строим точку O (				2	,−1) – центр
окружности и радиусом r = 2 1					1	3
окружности и радиусом r = 2 1					описываем окружность (рис. 14).
				3

Задача 32. Установить, какие линии определяются следующими уравнениями:

1) x2 + y2 −6x + 4 y +13 = 0 ;

2) x + y − x + 2 y +

2 = 0 ;

3) y = + 4 − x2 ;

"Н

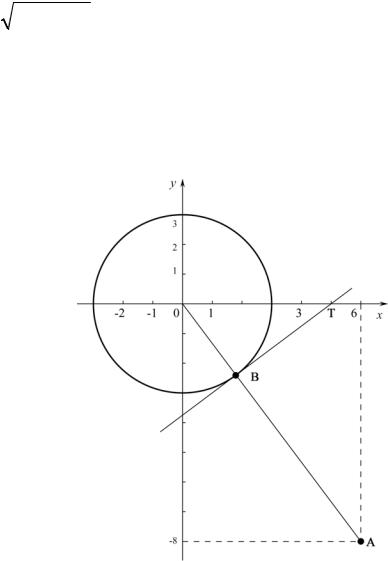
4) x = −2 − 9 − y

Изобразить, если возможно, эти линии на

Гчертеже.

Решение. 1. Представим уравнение втивиде

−6x +9) +( y

4 y +

4) = 0

илим(x −

+( y + 2)

= 0 .

.org

Так

как

ни один из

квадр

тов

(x −3)

( y + 2)

не

matem

может быть

отрицательным, то необходимое, чтобы

их сумма равнялась нулю

x −3 = 0 и y + 2 = 0а.

Откуда x =3, y =д−2 .

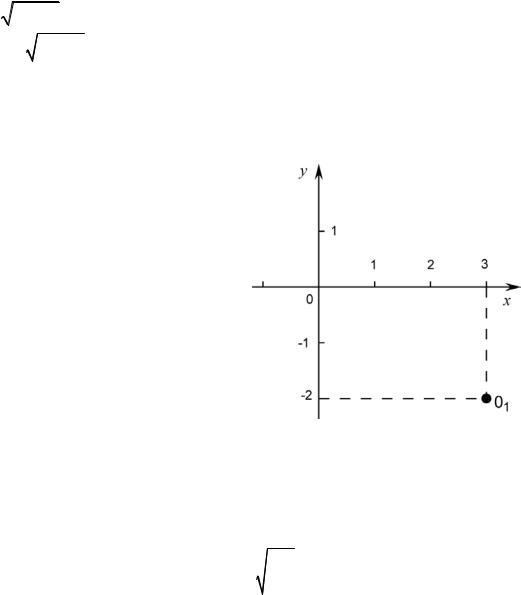
Данному

уравнениюф

удовле-

точка O1(3;−2) , и

творяет единственнаяК

это уравнение – окружность нулевого

радиуса r = 0 (рис. 15).

2. Представим данное уравнение в

виде

(x2 −2

x +

) +( y2 +2 1 y +1) = −

Рис. 15

или (x −

)

( y +1)

= −

уравнению

удовлетворяет ни одна

пара действительных

Этому

не

текущих координат, но ради общности считают, что уравнение выражает

мнимую окружность с радиусом r = −	3	(такую окружность на
	4

действительной плоскости OXY изобразить нельзя).

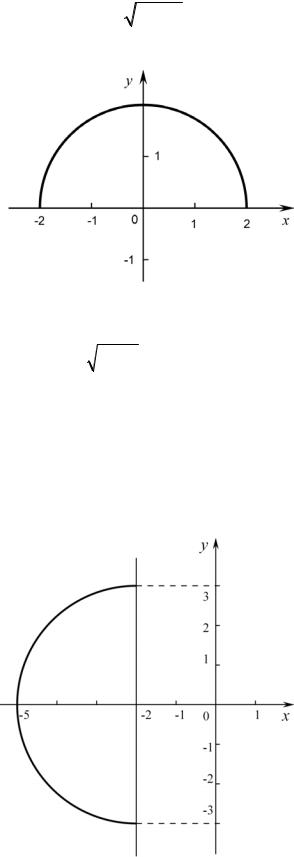
3. Этому уравнению удовлетворяют точки		с неотрицательными
ординатами		≤ x ≤ 2 , т.е.
точки верхней полуплоскости. Поскольку уравнение		легко преобразовать к
виду x2 + y2 = 4 , заключаем, что y =	4 − x2 есть уравнение верхней половины

окружности с центром в начале координат и радиусом r = 2 (рис. 16).

Рис. 16

4. Уравнению

x =−2 −

9 − y2

точки,

имеющие

удовлетворяюти

отрицательные абсциссы и ординаты, удовлетворяющиети

неравенству −3 ≤ y ≤3 ,

те

т.е. точки, лежащие в левой полуплоскостим .от прямой

= −2 . Это уравнение

org

+ y

=9 .

легко привести к нормальному уравнениюа

окружности (x + 2)

matem

Следовательно,

лежащую в

левой

оно определяет полуокружность,

полуплоскости от прямой

радиус

x = −2 и имеющую центр в точке (–2;0),

окружности r = 3 (рис. 17).

Рис. 17

Задача 33. Вычислить кратчайшее расстояние от точки А(6;–8) до окружности x2 + y2 =9 .

Решение. Точка А(6;–8) лежит вне окружности, так как ее расстояние от центра окружности

OA = 62 +(−8)2 =10 больше, чем радиус окружности r =OB =3 (рис. 18).

Радиус r перпендикулярен касательной BT к окружности в точке касания В. А поскольку он является частью прямой ОА , то AB BT . Следовательно, отрезок AB =OA −OB = 7 – кратчайшее расстояние точки А от окружности.

ти

те

org

matem

Рис. 18

Задача 34. Составить уравнение линии, сумма квадратов расстояний каждой точки которой от точек А(–1;0) и В(1;0) равна 4.

Решение.	Пусть точка	М(х, у) лежит на линии, тогда по условию
AM 2 + BM 2 = 4 .	Поскольку	AM 2 = (x +1)2 + y2 , BM 2 = (x −1)2 + y2 ,	то
(x +1)2 + y2 +(x −1)2 + y2 = 4 .		Откуда x2 + 2x +1 + y2 + x2 − 2x +1 + y2 = 4	или

x2 + y2 =1, т.е. искомой линией является окружность.

Задача 35. Составить уравнение линии, каждая точка которой находится от точки А(1;2) в два раза дальше, чем от точки В(–2;0).

Решение. Обозначим переменную точку линии через М (х, у), тогда по условию AM = 2BM , т.е.

(x −1)2 + ( y − 2)2 = 2 (x + 2)2 + y2 .

Возведя обе части последнего равенства в квадрат и раскрывая квадраты разностей и квадрат суммы, получим:

x2 −2x +1 + y2 −4 y + 4 = 4(x2 + 4x + 4 + y2 ) .

Далее складывая подобные, находим

3x2 +3y2 +18x + 4 y +11 = 0 .

Поскольку в последнем уравнении

A =C =3 и B = 0, то это уравнение определяет окружность.

Задача

36.

+6x −6 y +19

= 0

Показать,

что

уравнение

не

+ y

определяет никакого геометрического объекта.

Решение. Преобразуем уравнение

ти

+6x

+9) −9 + ( y

−6 y

+9) −

9 +19 = 0ua

те

или (x +3)2 +( y −3)2 = −1

а .org

matem

чисел не может быть отрицательным

Поскольку сумма неотрицательныхш

не удовлетворяют координаты ни одной

числом, то заданному уравнениюы

точки плоскости Oxy .

Задача

Найти

расстояние

между

центрами окружностей

37.

x2 + y2 +3x +8 y +12 = 0 .

Пересекаются

ли

эти

4x2 + 4 y2 + 20x +К9

= 0

окружности?

Решение. Приведем уравнение окружностей к нормальному виду, для чего выделим полные квадраты переменных:

1)4(x2 + 2 52 x + 254 ) −25 + 4 y2 +9 = 0 ; (x + 52)2 + y2 = 4 ;

2)(x2 + 2 32 x + 94) − 94 + ( y2 − 2 4 y +16) −16 +12 = 0 ; (x + 23)2 +( y +4)2 = 254 .

Следовательно, первая окружность имеет центр в точке O1(−52 ,0) , ее радиус r1 = 2 . Центром второй окружности служит точка O2 (− 32 , −4) , а радиус

= 2,5 . Расстояние O O =

(−

+(−4)2 =

17 ≈ 4,1 .

Поскольку

r1 + r2 = 2 + 2,5 = 4,5

больше

O1O2 = 17 ≈ 4,1, то

заданные

окружности пересекаются.

Задача 38. Написать уравнение кривой, сумма квадратов расстояний от

каждой точки которой до точек А(–а;0), В(0;а) и С(а;0) равна 3a2 .

Решение.

Пусть

– линия,

задачи;

удовлетворяющаяУ условиям

M ( x, y) Г в том и только в том случае, когда

MA + MB + MC =3a

или

3a .

(x + a) + y + x +( y − a) + (x − a) + yк=

После простых преобразований получаемти

уравнение

+ y

−

.ua

= 0

те

org

и, выделяя полный квадрат по переменной y , окончательно имеем

+( y −

)

matem

Это и есть искомоеауравнение кривой, являющейся окружностью радиуса

) .

с центром в точкееO (0;

2.2. Эллипс

Эллипс – это геометрическое место точек, сумма расстояний которых от двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Если постоянную сумму расстояний произвольной точки эллипса от фокусов F1 и F2 обозначить через 2a , а расстояние между фокусами через

2C(F1F2 = 2C) и оси декартовой прямоугольной системы координат выбрать

так, чтобы фокусы эллипса располагались на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид:

x2	+	y2	=1,	(18)
a2		b2

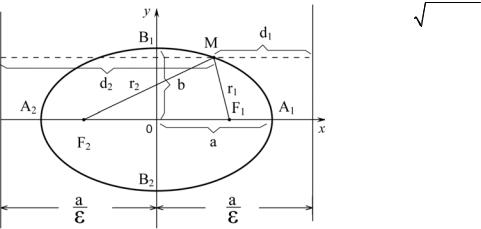
где b =

a2 −c2 ;

очевидно

a >b .

Уравнение

вида

(18)

называется

каноническим уравнением эллипса

(рис. 19).

Если

фокусы

эллипса

расположены на оси ОУ, то

уравнение эллипса имеет тот же

вид (18), но в этом случае

b > a .

Точки

A1(a;0), A2 (−a;0), B1(0;b)

B2 (0; −b) называются вершинами

Рис. 19

эллипса,

F1(c;0) и F2 (−c;0)

– его

фокусами,

отрезок

A1 A2 = 2a –

большой

осью

эллипса

(а

–

1 2

большая полуось), B B

= 2b – малой осью эллипса ( b – малая полуось).

Число ε = a ,

(19)

где а – большая полуось,

эллипса. Если

называется эксцентриситетомВ

a = b , то уравнение вида (18)

, рассматриваемую как

определяет окружностьи

(для окружности ε = 0 ).

частный случай эллипса. Для эллипса, очевидно, ε < 1

Отрезки F1M = r1

и F2 M = r2

называют фокальными радиусами точки М. Они

= a −мεx ,

(20)

rorg= a +εx .

могут быть вычислены по формулам: те

ен

a > b ,

Если эллипс

определ

уравнением

(18)

то

прямые,

перпендикулярные к фокальной осиmatemи отстоящие от центра на расстоянии

эллипса. Их уравнения:

называются директрисамир

x = −

x =

(21)

Если b > a , то директрисы определяются уравнениями

y = −

y =

Каждая директриса обладает следующим свойством:

=ε ,

(22)

где d1, d2

– расстояния произвольной точки M ( x, y) эллипса от

односторонней с соответствующим фокусом директрисы.

Множество точек М, отвечающих значениям параметра t

от 0 до 2π

удовлетворяющих уравнениям

x = a cos t

(23)

y = bsin t

представляет эллипс, в чем легко убедиться, исключая t из уравнений (23). В

самом деле, если точка

M ( x, y) такова, что

x = a cos t

и y = bsin t для

некоторого значения t [0;2π], то

x 2

y 2

= cos2 t +sin2 t =1, т.е. точка M ( x, y) принадлежит эллипсу.

Уравнения (23) называются параметрическими уравнениями эллипса.

Перенеся

центр

эллипса

точку

O1(x0 , y0 ) – начало новой системы

координат O1 XY , уравнение эллипса можно записать в виде

( x − x ) 2

( y − y

) 2

=1.

(24)

Раскрывая

квадраты

разностей в

получают общее

уравнении (24),

уравнение второй степени вида

+Cy

+ Dx + Ey + F = 0 ,

(25)

в котором A ≠ C, A C > 0

( A =

,Cк= b2

ти

Значит, при указанных значениях А и С уравнение (25), а в случае B = 0 и

уравнение (13)

могут определять эллипсте . В зависимости от значений D, E, F

эллипс

эти уравнения могут также определять мнимый.org

matem

( x − x0 )

( y − y0 )

= −1

вплоскости из уравнения

или точку ( x

)

на

( x

− x )

( y

− y

)

= 0 .

Задача 39. Составить уравнение эллипса, если его большая полуось равна 10, а эксцентриситет ε = 0,8 . Изобразить эллипс на рисунке.

Решение. Используем каноническое уравнение эллипса (18). Параметры a и c определяют из условия задачи:

2a =10 a = 5,

ε = ac = 0,8 c = 0,8a = 0,8 5 = 4.

По формуле b2 = a2 −c2 находим b2 :

b2 = 52 −42 = 9 .

Заменяя в формуле (18) a2 и b2 соответственно числами 25 и 9, получаем искомое уравнение эллипса

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.2016924.3 Кб237Bezopas_dvizhenia_rus_2.docx
#
18.09.201934.95 Кб1Bilet_vse_25.docx
#
24.04.20195.11 Mб2Bilyavskiy.doc
#
06.06.20151.34 Mб9BIS3_matem_org_ua.pdf
#
06.06.20151.4 Mб12BIS4_matem_org_ua.pdf
#
06.06.20151.77 Mб16BIS5_matem_org_ua.pdf
#
28.03.20162.42 Mб8book_full.pdf
#
15.11.2019564.21 Кб1Brif_dlya_konsultantov_ISTINNAYa_iyul_2012.docx
#
26.08.2019102.02 Кб2bukhuchet.docx
#
22.11.2019185.21 Кб2BYuDZhETUVANNYa_Rob_zoshit_dlya_studentiv.docx
#
06.06.2015755.71 Кб33ch5 в работе.doc