22

Міністерство освіти та науки, молодi та спорту України

Національний Гірничий Університет

Факультет інформаційних технологій

Кафедра системного аналізу та управління

Курсовая работа по дисциплине «МОДО»

На тему: «Исследование моделей линейного программирования на чувствительность»

Выполнила:

ст.гр.САит-11

Горбач Олеся

Проверил:

Лазорин А.И.

Днепропетровск 2014

Содержание

Введение

1. Математическая постановка задачи

   1. Графическое решение задачи ЛП

   2. Первая задача анализа на чувствительность

   3. Вторая задача анализа на чувствительность

   4. Третья задача анализа на чувствительность

2. Аналитическое решение задачи ЛП

   1. Оптимальное решение.

   2. Статус ресурсов.

   3. Ценность ресурса.

   4. Максимальное изменение запаса ресурса.

   5. Максимальное изменение коэффициентов удельной прибыли (стоимости)

3. Анализ модели на чувствительность

   1. Изменение правых частей ограничений

   2. Добавление нового ограничения

   3. Изменение условий задачи, влияющих на оптимальность решения

   4. Изменение удельных расходов ресурсов

   5. Добавление нового вида производственной деятельности

Вывод

Введение

На практике с задачами ЛП довольно часто приходится сталкиваться при анализе какого-либо вида производственной деятельности.

Формально модель является линейной, если и ограничения и целевая функция линейны. Но линейность предполагает также наличие таких свойств как пропорциональность и аддитивность.

Пропорциональность означает, что вклад каждой переменной в целевую функцию и общий объём потребления соответствующих ресурсов прямо пропорционален величине этой переменной.

Аддитивность заключается в том, что целевая функция представляет собой сумму вкладов от различных переменных. Аналогично левая часть ограничения должна представлять собой сумму расходов, каждое слагаемое которой пропорционально величине соответствующей переменной. Если, например, фирма производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на сбыте другого, то такая модель не обладает свойством аддитивности.

1. Математическая постановка задачи.

Математическую модель можно сформулировать следующим образом. Определить суточные объёмы производства x₁иx₂, при которых достигается

F= 4x₁+ 6x₂→maxучитывая ограниченияx₁– 2x₂ ≤ 2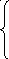

2x₁+x₂≥ 3

x₁+x₂≤ 7

x₂≤ 3

x₁,x₂≥ 0

1. Графическое решение задачи лп.

Так как модель содержит только две переменные, задачи можно решить графически. Для этого воспользуемся следующим алгоритмом:

1. На плоскости x₁0x₂ построим граничные прямые, уравнения которых получим путём замены неравенств в ограничениях на равенства.

2. Найдём допустимые полуплоскости. Например, условие x₁+x₂≤ 7

при x₁ = 0 и x₂ = 0. Значит точка (0,0) лежит в допустимой

полуплоскости.

3. Определим область допустимых решений – многоугольник АВСDE. В каждой точке, принадлежащей многоугольнику, все ограничения выполняются, поэтому имеем бесконечное множество допустимых решений, но, несмотря на это, можно найти оптимальное решение, если выяснить, в каком направлении возрастает целевая функция F = 4x₁ + 6x₂ .

4. Для этого строим вектор с( 4;6 ).

5. Строится прямая 4x₁+6x₂= 0, перпендикулярная вектору с, которая передвигается в направлении вектора с до тех пор, пока она не достигнет области недопустимых решений. Из рис.1 видно, что оптимальному решению соответствует точкаD. Так как точкаDявляется точкой пересечения прямыхx₁+x₂=7и x₁ – 2 x₂ = 2, то значенияx₁иx₂в этой точке определяются решением системы из этих двух уравнений, которое даёт следующий результат:x₁ =,x₂ =. Это значит, что суточный объём производства товара должен бытьтонны, а товараx₂-тонны. Доход в этом случае составит

F = тысяч долларов.

Рис.1 Область допустимых решений