Свойства проекции вектора на вектор

1) Прrλar

= λПрrar

b

b

+ Прrcr

2) Прr (ar

+ cr) = Прrar

b

b

b

аr

аr +b

Скалярным произведением векторов а и b наз. скаляр , обозначаемый ar b и равный

произведению их модулей на косинус угла между ними, т.е.

ar br = аr br cos(ar,br)

( 1 )

Скалярное произведение векторов a и b

и

их

проекции друг на друга связаны

соотношениями

r

r

r

r

r

r

( 2 )

a

b

=

a

Прarb

=

b

Прbra

ar b = b ar

СВОЙСТВА СКАЛЯРНОГО ПРИЗВЕДЕНИЯ.

1)

(коммутативность)

2)

(λ ar) br = λ

(ar br)(ассоциативность)

3)

ar(br + cr)= arbr

+bcr (дистрибутивность)

r

b , тогда

r

r

r

r

π

=

r

r

0

= 0 .

Пусть нам известно , что a

a

b =

а

b

cos

a

b

Ч.Т.Д.

2

ОПР 2

Скалярное произведение вектора a самого на себя называется

скалярным квадратом и

обозначается

аr2

ТЕОРЕМА 3 (Теорема о скалярном квадрате)

Скалярный квадрат вектора равен квадрату его модуля , т.е. :

Доказательство:

аr2

=

аr

2

(3)

аr2

= аr аr =

аr

аr

cos 0 =

аr

2

ПРИМЕР:

ar +b

ar −b ,

Какому условию должны удовлетворять векторы

и

чтобы они были

перпендикулярны?

(ar +b )(ar −b )= 0 , ar2 −b 2

= 0 , ar2

= b 2

теорема 3

r

2

=

r

2

,

r

=

r

a

b

a

b

Ответ : для этого достаточно , чтобы

r

=

r

a

b

3)ортогональный и нормированный базис называется ортонормированным или

Декартовым .

В декартовом базисе базисные орты обозначаются :

ir,

rj, kr.

r

r

r

.

r

r

r

r

r

=

r

=

i

j,

j

k , i

k ,

i

j

k

=1

a

x

= Прrar

a

у

= Прrar

a

z

= Прrar

i

j

к

Доказательство:

rj + a

kr)=§ 6 , 2 свойство =

Прrar

= Пр

(a

ir

+ a

i

i

x

ry

z

r

= § 6 , 1свойство=

Пр.r a

i + Пр.r a

j

+ Пр.r a

k

i

x

i

y

i

z

r

= ax Пр.ir i + ay Пр.ir

j + az Пр.ir k =§ 6 , определение=

ir

1

1

rj

0

kr

0

= ax

cos 0 + ay

cos90o + az

cos90o = ах

ar +br = {ax +bx , ay +by , az +bz }

ar −br = {ax −bx , ay −by , az −bz }

λar = {λax ,λay , λaz }

Доказательство:

r

r

r

r

r

r

j +bz k = § 4 , опр.5, 3 сво-во=

a

+b

= ax i

+ ay j

+ az k

+bx i +by

(ax +bx )ir + (ay +by )rj +(az +bz )k

ОПР 1

z

Введем следующие обозначения :

ar

α = (arx)

, β = (ary) , γ = (arz)

Тогда

γ

cosα , cos β, cosγ - называются

β

направляющими косинусами вектора.

в декартовом базисе , равно сумме произведений их соответствующих координат

rv

= axbx + ayby

+ az bz

(1)

ab

Доказательство:

ir2

= rj 2

Отметим еще раз , то что

= k 2

=1 ,

i j = jk = ki

= 0

arbr

= (ax ir + ay

rj + az kr)(bx ir

+by rj +bz k )= 0

0

rr

= a

b

r

+ a

b

r

+ a

b

r

b

+a

b

)i j + (a b + a

b

)i k + (a

b

+ a

b

=

x

i

2

у

у

j 2

z

k 2 + (a

x

y

y

x

x

y

)jk

x

z

x z

z

z

y

z

= axbx

+ a y by

+ az bz

Получается (1), ЧТД

ТЕОРЕМАU

3U (Теорема Пифагора)

ar = axi + ay j + az k

В Декартовом базисе модуль вектора

равен

ar =

ax

2 + ay

2 + az

2

(2)

Доказательство:

ar =

ar 2 =§ 7 , Т 3 =

ar2

= (1) =

ax ax

+ a y a y

+ az az =

ax

2 +ay

2 +az

2 = ЧТД

ТЕОРЕМАU

4

rU

Координаты a в декартовом базисе можно записать следующим образом :

ax =

ar

cosα ,

ay

=

ar

cosβ ,

az =

ar

cosγ

(3)

Доказательство:

= Прirar =

ar

cos (ar,i ) = опр.1 =

ar

cos (ar, x) =

ar

По Теореме 1 §8

, ax

cosα ,

ЧТД.

ТЕОРЕМАU

5U

Координаты

единичного вектора равны его направляющим косинусам

Если

nr

=1

, то

nr

=

{cosα,cos β,cosγ}

0

0

cosα =

ax

;

cos β =

ay

ax 2 +ay 2 +az 2

ax 2 + ay 2 + az 2

cos γ

=

az

ТЕОРЕМАU

7

Сумма квадратов направляющих косинусов равна 1 , т.е.

cos2 α +cos2 β +cos2 γ =1

(5)

ТЕОРЕМАU

8U (угол между векторами)

и b ={bx ;by ;bz } в декартовом базисе

Косинус

угла

между

векторами a = {ax ;ay ;az }

находится по следующей формуле:

r

r

axbx

+ayby +az bz

(6)

cos (a;b )=

az 2 +ay 2 +ay 2 bx 2 +by 2 +bz 2

Доказательство:

cos (ar;br)

cos (ar;br)=

ar

По опр. 1 §7

arbr =

ar

br

br

подставляя сюда (1) и (2) §9

r

получаем

axbx

+ayby +az bz

a

b

r

r

,

ЧТД.

cos (a;b )=

az 2 +ay 2 +ay 2 bx 2 +by 2 +bz 2

ТЕОРЕМАU

9 U (условие перпендикулярности векторов)

В декартовом базисе условие перпендикулярности векторов ar ={ax ;ay ;az }и br ={bx ;by ;bz }

имеет вид :

(7)

axbx

+ a y by + az bz

= 0

Доказательство:

§ 7 ,

Согласно Теор.2

если векторы перпендикулярны,

то их скалярное произведение

равно 0 . Следовательно, из формулы (1) данного параграфа вытекает (7)

ТЕОРЕМАU

10U (Условие коллинеарности 2-х векторов )

Два

вектора

ar ={ax ;ay ;az }

и b ={bx ;by ;bz } коллинеарны, если их соответствующие

координаты пропорциональны

ar

=

a

x

=

ay

=

a

z

= λ

(8)

r

bx

by

bz

b

Доказательство:

Пусть ar

br, тогда § 4, опр.5

ar =λb , но λb = {λbx ; λby ; λbz }, приравнивая между собой

соотв. координаты получаем ax = λbx ,

ay = λby ,

az = λbz , откуда получается (8).

ТЕОРЕМАU

11U (координаты вектора, заданного точками начала и конца)

Если

M1 (x1 y1z1 ) и M 2 (x2 y2 z2 ) , то M1M 2 (x2 − x1 , y2 − y1 , z2 − z1 );

Т.е. из координат конца вектора вычитаются соответствующие координаты начала .

Доказательство:

Согласно опр.4 §8

z

OM1 ={x1, y1, z1}

M2B B

M1B B

OM 2 ={x2 , y2 , z2 }

Согласно определению суммы векторов

0

y

OM 2 =OM 1 +M1M 2

OM 2 −OM 1 = M1M 2 ,согласно теореме1 получаем

x

то,ЧТД.

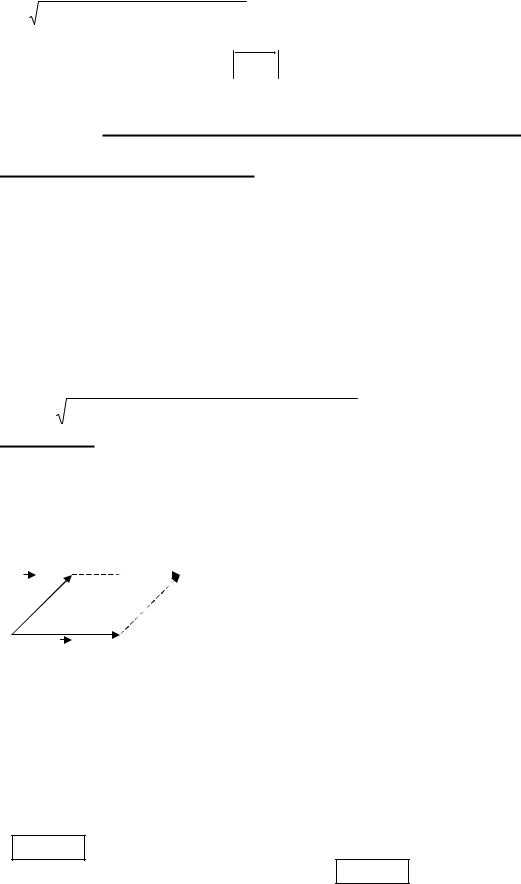
ТЕОРЕМАU

12

(x1 y1z1 ) и M 2 (x2 y2 z2 )

Расстояние между 2-мя точками , расстояние d,между точками M1

определяется по формуле:

d = (x2 − x1 )2 +(y2 − y1 )2 +(z2 − z1 )2

(9)

Доказательство:

обозначаемый как аr×b и в декартовом базисе вычисляемый по формуле:

r

r

=

ir

rj

kr

(1)

a

×b

ax

a y

az

bx

by

bz

Lля нахождения координат и модуля этого вектора разложим (1) по элементам 1-ой

строки:

аr×b = (aybz −az by )i +(az bx −axbz )j +(axby −ay bx )k

(2)

(2)- это разложение векторного произведения по базисным ортам i , j,k . Тогда

аr×br

= (ay bz −a z by )2 +(azbx −axbz )2 +(axby −ay bx )2

(3)

ТЕОРЕМАU

1U (О модуле векторного произведения)

ar×br

=

ar

br

sin (ar;br)

(4)

b

S

a

ТЕОРЕМАU

2U (Направление векторного произведения)

r

r

Векторное произведение а

×b перпендикулярно плоскости , в которой лежат вектора a и

brr иrнаправлено по правилу правой руки:

а-указательный палец, br

-средний палец, тогда

а×b - большой палец.

Доказательство:

Найдем скалярное произведение

ar (ar×b) = (1) §9 = ax (aybz −azby )+ay (az bx

−axbz )+az (axby −aybx )=

= ax aybz

− ax azby + ay azbx −ax aybz + ax azby − ay azbx = 0

r

r

r

a

а

×b

А

S

С

r

SABC=1/2SB

ABCD=1/2B

r

=1/2

AB × AC

а

×b

AB ={−2;3;1 }

AC ={−1;−1;−1}

AB × AC =

ir

rj

kr

= −2ir−3rj +5kr

−2 3 1