§ 1.3. Монотонные последовательности

1.3.1. Предел монотонной ограниченной последовательности

Определение. Последовательность называетсявозрастающей (убывающей), если при любом выполняется неравенство(). Последовательностьназываетсяневозрастающей (неубывающей), если при любом выполняется неравенство(). Во всех этих случаях последовательность называетсямонотонной.

Теорема. Неубывающая ограниченная сверху последовательность имеет предел.

Доказательство. Пусть последовательность неубывающая ограниченная сверху. Тогда найдётся такое числочто при всехвыполняется неравенствот.е. множество членов последовательности ограниченно сверху, значит, имеет супремумПокажем, чтоДействительно, по определению супремума при всехвыполняется неравенствои для любогонайдётсятакое, чтоТогда при всехимеемт.е.Теорема доказана.

Кроме того, мы доказали, что предел неубывающей ограниченной последовательности не меньше каждого её члена.

Следствие. Невозрастающая ограниченная снизу последовательность имеет предел.

Доказательство. Если последовательность невозрастающая ограниченная снизу, то последовательностьнеубывающая ограниченная сверху. Следовательно, существуетТогда существует и

1.3.2. Бесконечно большие последовательности

Определение. Последовательность называетсябесконечно большой, если для любого найдётсятакое, что при всехвыполняется неравенствоПри этом говорят, что пределравен бесконечности:

Если для любого найдётсятакое, что при всехвыполняется неравенството

Если для любого найдётсятакое, что при всехвыполняется неравенството

Теорема. Если последовательность неубывающая неограниченная сверху, то

Доказательство. Так как последовательность неограниченная сверху, то для любогонайдётсятакое, чтоТогда, т.к.неубывающая, при всехвыполняются неравенстваЗначит,

Аналогично, если последовательность невозрастающая неограниченная снизу, то

Таким образом, справедлива общая теорема о монотонных последовательностях.

Теорема. У монотонной последовательности существует предел, конечный или бесконечный.

1.3.4. Число е

Числом сочетаний из элементов по(обозначается) называется количество способов выбрать из множества, состоящего изэлементов, подмножество, состоящее изэлементов,Справедливо равенство, называемоебиномом Ньютона

Теорема-определение. Последовательность 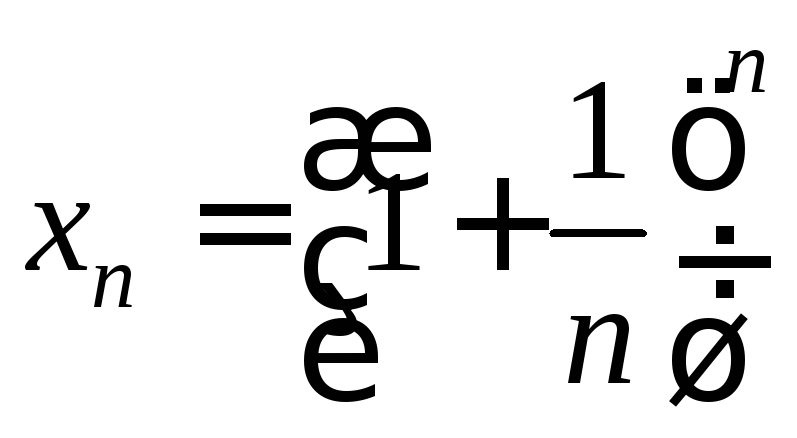имеет предел, и этот предел называется числом е.

Доказательство. Для того, чтобы доказать, что последовательность имеет предел, покажем, что она возрастает и ограниченна сверху. По формуле бинома Ньютона имеем

Тогда

Очевидно, что все слагаемые, начиная со второго, в меньше соответствующего слагаемого впоследовательностьявляется возрастающей.

Так как

то последовательность является ограниченной.

Следовательно, существует Теорема доказана.

Таким образом, согласно определению,

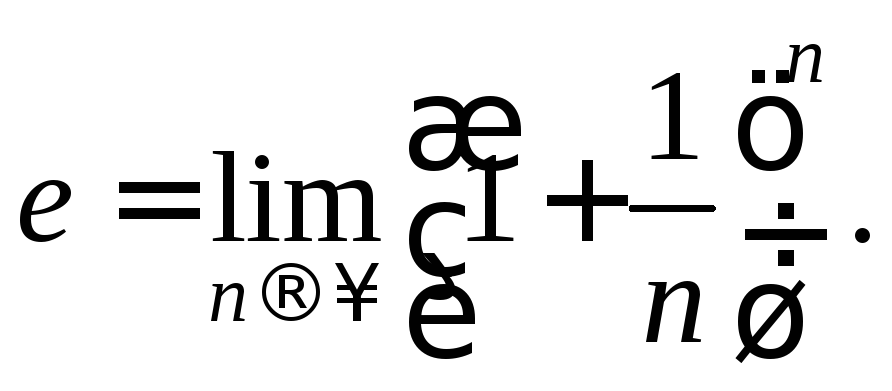
1.3.5. Теорема о вложенных стягивающихся отрезках

Определение. Система отрезков называется системой вложенных стягивающихся отрезков, если при любоми

Теорема. Система вложенных стягивающихся отрезков имеет единственную общую точку.

Доказательство. Так как то последовательностьявляется неубывающей. Кроме того, для любоговыполняется неравенствоследовательно, последовательностьявляется ограниченной. Следовательно, существуетТак как для любыхивыполняется неравенствотоКроме того,значит,при любомТаким образом,является общей точкой всех отрезковПредположим теперь, что общих точек две -иТак кактоНозначитТеорема доказана.