- •Часть 3. Системы дифференциальных уравнений.
- •Занятие 13. Системы дифференциальных уравнений в нормальной форме. Понятие общего решения. Задача Коши для системы. Решение системы сведением к одному ду более высокого порядка.
- •Занятие 14. Решение системы ду методом Эйлера.
- •Занятие 15. Решение системы дифференциальных уравнений: методом неопределённых коэффициентов и методом вариации произвольных постоянных.
- •Занятие 16. Исследование устойчивости решений однородных систем с постоянными коэффициентами. Исследование устойчивости по первому приближению.
- •Исследование устойчивости по первому приближению
Исследование устойчивости по первому приближению
Теперь, для придания общности используемым алгебраическим выражениям, не теряя их компактности, рассмотрим систему 3-х дифференциальных уравнений 1-го порядка:
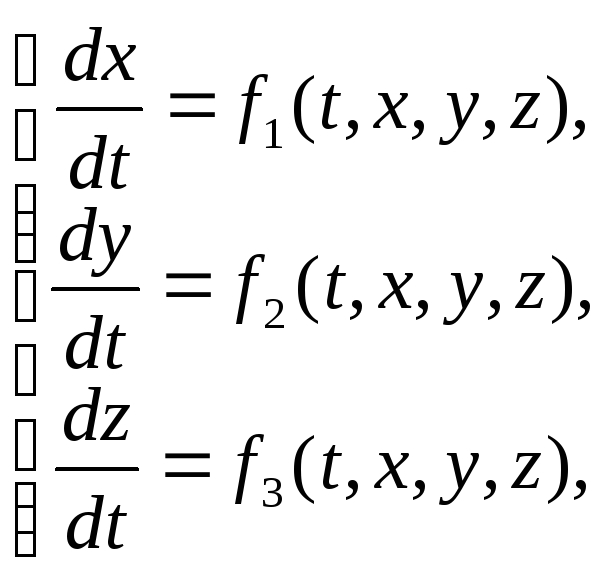 (3)
(3)
где функции
![]() ,
,![]() ,
,![]() имеют непрерывные производные по
переменным
имеют непрерывные производные по
переменным
![]() ,
причём вдоль тривиального решения:
,
причём вдоль тривиального решения:
![]() ≡0,
≡0,
![]() ≡0,
≡0,
![]() ≡0
эти производные постоянны, то есть:
≡0
эти производные постоянны, то есть:
![]() =
=![]() ,
,
![]() =
=![]() ,
, ![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() ,
, ![]() =
=![]() , (4)
, (4)
![]() =
=![]() ,
,
![]() =
=![]() ,
, ![]() =
=![]() ,
,
где коэффициенты
![]() – действительные числа (постоянные). В
сделанных предположениях для функций:
– действительные числа (постоянные). В
сделанных предположениях для функций:
![]() ,
,![]() ,
,![]() можем воспользоваться разложением в
ряд Тейлора:
можем воспользоваться разложением в
ряд Тейлора: ![]() =
=![]() +
+![]() ,
,
![]() =
=![]() +
+![]() , (5)
, (5)
![]() =
=![]() +
+![]() ,
,
где
![]() ,
,![]() ,
,![]() – бесконечно малые порядка выше первого
в окрестности точки:
– бесконечно малые порядка выше первого
в окрестности точки:
![]() .
Перепишем систему (3),
применяя выражения (5):
.
Перепишем систему (3),
применяя выражения (5):
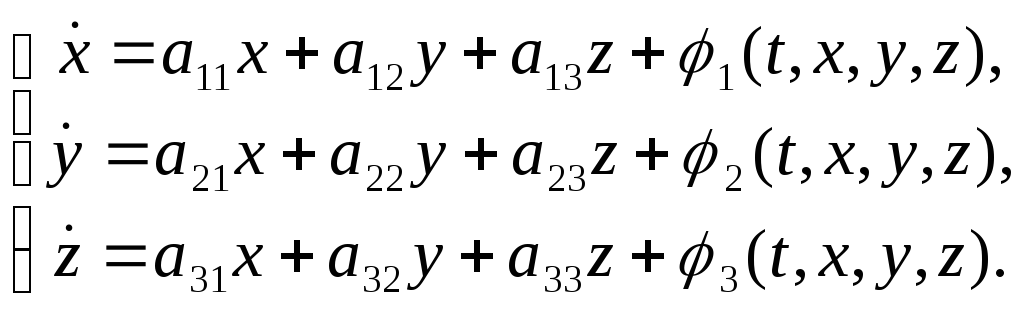 (6)
(6)
Замечание: Так как системы (3) и (6) эквивалентны, то решение вопросов устойчивости для них одинаково: если решение устойчиво для (3), то оно устойчиво и для (6)!
Теперь введём в
систему уравнений «неточность»: отбросим
бесконечно малые φ1,φ2,φ3
и заменим систему (6)
системой: 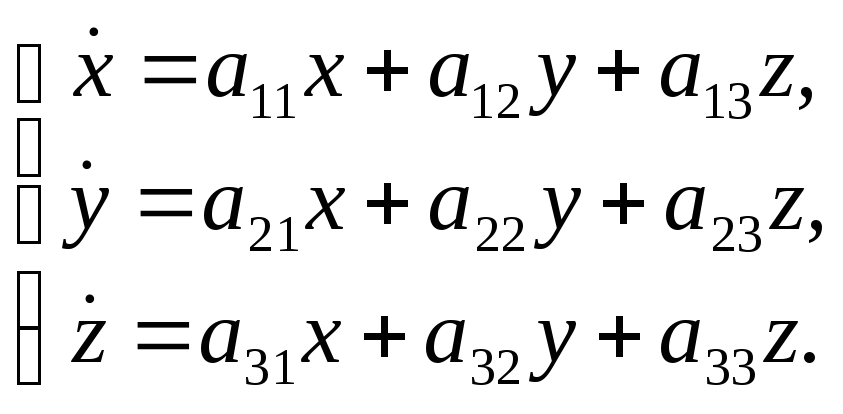 (7)
(7)
Систему (7) называют системой первого приближения для нелинейной системы дифференциальных уравнений (3).
Замечание: До Ляпунова при исследовании вопроса об устойчивости ограничивались в основном изучением устойчивости в первом приближении, считая, что полученный результат можно отнести и к исходной, нелинейной, системе. Ляпунов показал, что в общем случае это неверно, в то же время он дал ряд примеров нелинейных систем, для которых вопрос об устойчивости решается до конца по первому приближению!
Запишем без
доказательства теоремы, которые наглядно
показывают, как используются определённые
в выражениях (3)-(7)
величины.
![]()
|
Теорема: (14.1) |
Если:
1)
корни характеристического уравнения
системы (5)
имеют
отрицательную действительную часть,
и для функций
2)
|
Замечание: Очевидно, что если тривиальное решение устойчиво для системы (6), то оно устойчиво и для системы (7), причём асимптотически. В таком случае имеем: если тривиальное решение однородной системы (7) устойчиво, то оно устойчиво асимптотически!
Так же наглядно применение теоремы, определяющей достаточные условия неустойчивости решений системы:
|
Теорема: (14.2) |
Если:
1)
хотя бы один корень характеристического
уравнения системы (5)
имеет
положительную действительную часть,
и для функций
2)
|
Если у нескольких характеристических корней, не являющихся кратными, действительные части равны нулю, а у остальных отрицательные, то движение будет устойчивым, но не асимптотически. Если среди корней имеются кратные, то устойчивости, в общем случае, не будет, даже если у остальных вещественная часть отрицательна!
Использование
результатов теорем становится особенно
наглядным, если применить классификацию
точек покоя по тому, как «ведут себя
траектории возмущённого движения» в
окрестности этих точек. Для изображения
траекторий движения на плоскости
![]() в окрестности точки покоя воспользуемся
системой дифференциальных уравнений:
в окрестности точки покоя воспользуемся
системой дифференциальных уравнений:
 →
→ 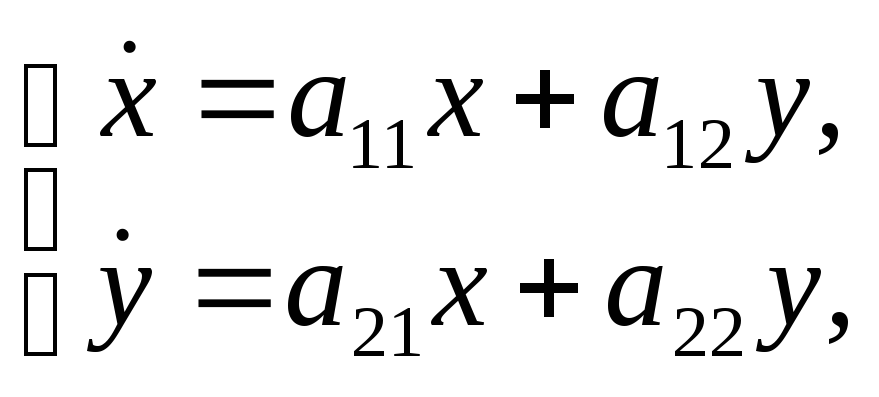 (8)
(8)
при начальных
условиях:
![]() =0,
=0,![]() =0.
=0.
В соответствии с теоремами об устойчивости решений имеем аналитическая характеристика точек покоя:
▪ если ни один из корней k1, k2 характеристического уравнения не лежит справа от мнимой оси, причем хотя бы один корень отличен от нуля, то решение устойчиво;
▪ если же хотя бы один корень лежит слева от мнимой оси или оба корня равны нулю, то решение неустойчиво.
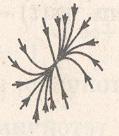
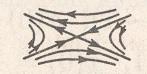
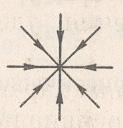
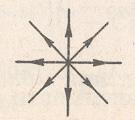
На рисунках, представленных в таблице 1, легко видим геометрические характеристики точек покоя:
▪ если точка покоя устойчива, то при небольших отклонениях от нее с течением времени движущаяся точка возвратится в точку покоя;
▪ если точка покоя неустойчива, то при небольших отклонениях от нее с течением времени движущаяся точка удалится от точки покоя как угодно далеко.
В таблице 1 представлен случай, когда характеристические корни системы ДУ действительны и различны, определена устойчивость системы решений и название точки покоя в соответствии с принятой классификацией.
Таблица 1
|
Корни
|
Характер точки покоя |
Устойчивость точки покоя |
|
Устойчивый узел |
|
Асимптотически устойчива. |
|
Неустойчивый узел |
|
Неустойчива. |
|
Седло |
|
Неустойчива. |
В таблице 2 представлен случай, когда характеристические корни системы ДУ комплексные (сопряжённые), определена устойчивость системы решений и название точки покоя в соответствии с принятой классификацией.
Таблица 2
|
Корни
|
Характер точки покоя |
Устойчивость точки покоя |
|
. Устойчивый фокус |
|
Асимптотически устойчива. |
|
Неустойчивый фокус |
|
Неустойчива. |
|
Седло |
|
Устойчива. |
В таблице 3 представлен случай, когда характеристические корни системы ДУ действительные кратные, определена устойчивость системы решений и название точки покоя в соответствии с принятой классификацией. Так как для создания «зрительного образа» мы рассматриваем только системы ДУ 2-го порядка, то кратность комплексных корней не рассматриваем.
Таблица 3
|
Корни
|
Характер точки покоя |
Устойчивость точки покоя |
|
Устойчивый узел
|
|
Асимптотически устойчива. |
|
|
||
|
Неустойчивый узел |
|
Неустойчива. |
|
|
Рассмотрим несколько Примеров исследования устойчивости, начав с линейных систем вида (7), которые могли бы быть результатом линеаризации некоторой нелинейной системы дифференциальных уравнений вида (3).
••• ≡ •••
Пример
1–456:
Исследовать устойчивость решения
системы в точке покоя:
![]()
Решение:
1). Найдем
характеристические корни заданной
однородной системы дифференциальных
уравнений: ∆(k)=![]() =0,
откуда получаем:
=0,
откуда получаем:
![]() =
=![]() =
=![]() .
.
2). Так как α>0, β≠0, то система неустойчива: неустойчивый фокус.
Ответ: система неустойчива: неустойчивый фокус.
Пример
2–458:
Исследовать устойчивость решения
системы в точке покоя:
![]()
Решение:
1). Найдем
характеристические корни заданной
однородной системы дифференциальных
уравнений: ∆(k)=![]() =0,
откуда получаем:
=0,
откуда получаем:
![]() =
=![]() =
=![]() .
.
2). Так как α>0, β≠0, то система неустойчива: неустойчивый фокус.
Ответ: система неустойчива: неустойчивый фокус.
Пример
3–460:
Исследовать устойчивость решения
системы в точке покоя:
![]()
Решение:
1). Найдем
характеристические корни заданной
однородной системы дифференциальных
уравнений: ∆(k)=![]() =0,
откуда получаем:
=0,
откуда получаем:
![]() =
=![]() .
.
2).
Так как корни
![]() ,
то система
асимптотически устойчива: устойчивый
узел.
,
то система
асимптотически устойчива: устойчивый
узел.
Ответ: система неустойчива: устойчивый узел.
Пример
4–462:
Исследовать устойчивость решения
системы в точке покоя:
![]()
Решение:
1). Найдем
характеристические корни заданной
однородной системы дифференциальных
уравнений: ∆(k)=![]() =0,
откуда получаем:
=0,
откуда получаем:
![]() =
=![]() .
.
2). Рассмотрим поведение системы в зависимости от значений параметра α:
▪ пусть
корни действительные:
![]() ,
,
![]() <
0 →
<
0 →
![]() и
и
![]() <
<![]() → можно неравенство возвести в квадрат:
→ можно неравенство возвести в квадрат:
![]()
![]() ,
откуда:
,
откуда:
![]() ,
но
,
но
![]() не имеет решения → обеспечить устойчивость
невозможно;
не имеет решения → обеспечить устойчивость
невозможно;
▪ пусть
корни действительные:
![]() =
=![]() →
→
![]() → это требует
→ это требует
![]() =0,
или
=0,
или
![]() =4
при условии:
=4
при условии:
![]() → такое невозможно → и в этом случае
обеспечить устойчивость невозможно;
→ такое невозможно → и в этом случае
обеспечить устойчивость невозможно;
▪ пусть
корни комплексные:
![]() =
=![]() .
Необходимо выполнение условий
.
Необходимо выполнение условий
![]() → это требует (2-е неравенство: метод
интервалов!)
→ это требует (2-е неравенство: метод
интервалов!)
![]() при условии первого неравенства:
при условии первого неравенства:
![]() → такое невозможно → и в этом случае
обеспечить устойчивость невозможно;
→ такое невозможно → и в этом случае
обеспечить устойчивость невозможно;
Ответ:
устойчивость системы за счёт выбора
параметра
![]() обеспечить не удалось.
обеспечить не удалось.
Вопросы для самопроверки:
-
Каково назначение раздела теории ДУ: теория устойчивости?
-
Что такое: невозмущённое движение и возмущённое движение?
-
Что такое точка покоя?
-
Что значит: устойчивость тривиального решения системы?
-
Какие случаи устойчивости точки покоя реализуются, если характеристические корни системы действительные, разные?
-
Какие случаи устойчивости точки покоя реализуются, если характеристические корни системы комплексные?
-
Какие случаи устойчивости точки покоя реализуются, если характеристические корни системы действительные, кратные?
-
Как случаи устойчивости точки покоя изображаются на комплексной плоскости?
☺☺