Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Михайлов ТФКП практикум2013

.pdf

Скачиваний:

1470

Добавлен:

05.06.2015

Размер:

3.91 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2517 18 19 20 21 22 23 24 25 > Следующая >>>

			1			1
I = ∫ (1+ z + z2 )e z dz + ∫						(1+ z + z2 )e		dz +
I = ∫ (1+ z + z2 )e z dz + ∫						(1+ z + z2 )e	z−1	dz +
	z	=3		z	=3
	z	=3		z	=3

+ ∫ (1+ z + z2 )e z−2 dz = I1 + I2 + I3.

z =3

Сосчитаем эти три интеграла. Подынтегральная функция в интеграле I1 имеет одну особую точку внутри контура интегрирования

z = 0 (существенно особая точка). Разложим функцию в ряд Лорана в этой точке:

∞

f (z) = (1 + z + z

)e z = (1 + z + z

) ∑

n=0 n! z

= (1 + z + z2 )

1 +

+... .

3!z

Соберем все коэффициенты при 1z :

c−1 =1+ 12 + 3!1 = 53 .

Таким образом, I1 = 2πi 53 .

Аналогично поступим, вычисляя интеграл I2 , подынтегральная функция в котором содержит также одну особую точку z =1 .

Предварительно многочлен 1 + z + z2

представим в виде многочле-

на по степеням z −1:

1+ z + z2 =1+(z −1) +1+ (z −1)

+1 2

= (z −1)2

+3(z −1) +3.

Разложение в ряд Лорана в точке z =1 будет иметь вид:

∞

f (z) = (1 + z + z2 )e z−1 = (z −

+3(z −1) +3 n∑=0

(z −1)n

= (z −1)2 +3(z −

1) + 3

1 +

+... .

z −1

2 (z −1)2

3!(z −

1)3

161

Опять соберем коэффициенты при z −1 , чтобы получить c−1 : res[ f (z),1] = c−1 = 3 + 32 + 3!1 = 143 .

Следовательно I2 = 2πi 143 . Действуя таким же образом, най-

дем, что интеграл I3 = 2πi 293 . Окончательно получим

I= 2πi 5 +14 + 29 = 32πi .

3 3 3


Пример 11.7 ([3], № 4.127).			1		C∫		dz	, где С – окруж-
Пример 11.7 ([3], № 4.127).				2πi	C∫	z2 + z +1		, где С – окруж-
ность	z	= r ≠ 1 .	1
ность	z	= r ≠ 1 .
Решение. Функция f (z) =							– двузначная. Однако в
Решение. Функция f (z) =			z2 + z +1				– двузначная. Однако в

окрестности точки z = 0 она допускает разделение на две независимые однозначные аналитические ветви, отличающиеся знаком, так как точка z = 0 не является точкой ветвления этой функции. Особыми точками функции являются ее точки ветвления, которые найдем, приравняв подкоренное выражение нулю:

z2 + z +1 = 0	z	=	−1±i 3	.

	1,2		2

Оба корня по модулю равны единице. Поэтому, если радиус контура интегрирования r < 1, то внутри контура особых точек нет, и интеграл от каждой из двух ветвей равен 0. Если r > 1, то вне контура особых точек нет, но вычет в бесконечно удаленной точке не равен нулю, так как при z →∞

f (z) =		1	±	1	,
	z2	+ z +1		z

res[ f (z),∞] = −c−1 = ±1.

Как известно, контурный интеграл, вычисляемый по внешним точкам, равен

162

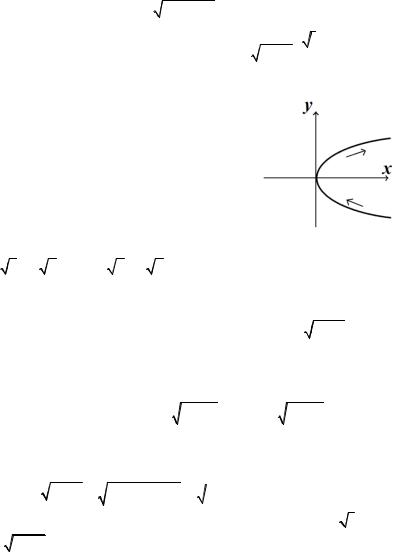
−2πi∑res[f ( z), zk ],

где zk – особые точки вне контура. В данном случае (при r >1)

C∫

= ±1.

2πi

z2 + z +1

Пр имер 11.8 ([3], № 4.128).

∫

(

=1)

, где С –

2πi

(

)

парабола y2 = x , обходимая в

сторону возрастания у.

Решение. Контур С можно

рассм атри-

вать как замкнутый, проходящий через

бесконечно

удаленную

точку,

которой

ветви параболы замыкаются (рис. 11.1).

Бесконечность – правильная точка для обе-

их ветвей подынтегральной функции. Най-

дем особые точки, попадающие внутрь

контура, приравняв нулю многочлен z4 +1 .

Получим

две

точки

внутри

контура

Рис. 11.1

и z

– пол юсы первого порядка. Вычеты

z =

−i

вычислим по формуле

, приняв за φ функцию

, а за ψ

ψ′

z2 +

функ цию

z4 +1 ;

z1,2

res f (z), z

= 1

4z3 z2 +1

1,2

z4 z2 +1

1,2

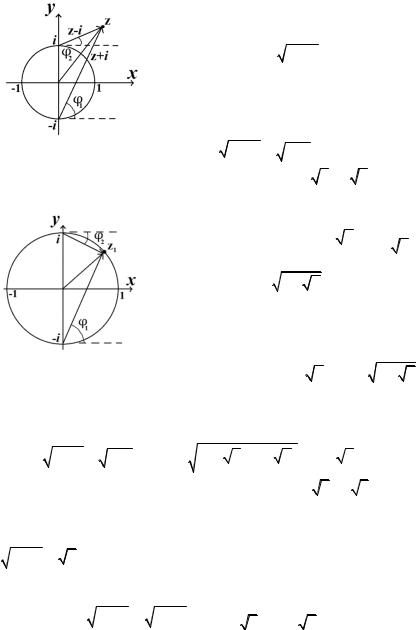
где

z4 = −1 .

Обозначим

z +i = ρ eiφ1 ,

z −i = ρ

eiφ2 .

По определе-

1,2

нию корня

+φ2 +2πk

i φ1

)

z2 +1 =

z +i

z −i

(

= 0,1

ρρ

Так как для выбора одной ветви из двух дано условие

1 =1 , то

есть

z2 +1

z=0

=1, то при z = 0

z +i

= ρ eiφ1

имеем

163

ρ =1; φ =

, z −i = ρ

eiφ2

ρ2 =1; φ2

= −

+1 = eiπk

=1 k = 0

(рис. 11.2).

Следовательно, мы должны рассматри-

вать ветвь корня, задаваемую выражением

φ +φ

Рис. 11.2

z2 +1 =

ρρ

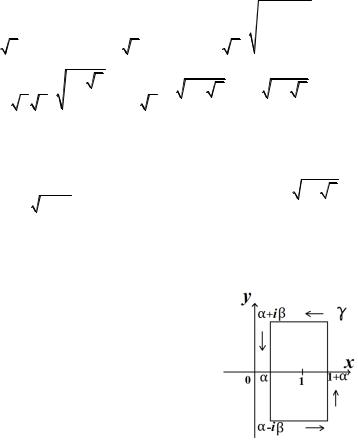
Вычислим значение этой ветви в точке

. Вектор

z +i

имеет в этой точке модуль

ρ2

−2cos

3π

= 2 + 2

= 2 +

2 ,

ρ1 =

2 +

2 ,

его

аргумент

3π

(рис.

11.3),

вектор

z −i

Рис. 11.3

имеет в этой точке модуль

ρ22 =1+1−

2cos

= 2 −

2 ,

ρ2

2 −

2 ,

его аргумент φ2

= −

. Получаем, что

φ +φ

(

)(

)

ei 1 2 2

= 4

−

2 +

ei 8 = 4 2

ei 8 .

z2 +1 =

ρρ

Аналогично

рассматривается

точка

z = z2

−i

Ввиду

симметрии этих двух точек относительно оси х сразу получаем, что

z22 +1 = 4 2 e−i

. Для суммы вычетов получим значение:

e−i

−

= −

2 e

−i

164

	1		i	π			π			1			π		1		1+cos		π
						−i						2cos							4
= −			e 8		+e		8	= −						= −						=
		2									2		8		24	2		2
4	4								4	4
= −			1		1+			2	= −		1		2 +		2 = −		1	1+ 2 .
	24 2 2							2			24 2 2						4

Так как по условию обход контура происходит по часовой стрелке (т.е. в отрицательном направлении), то надо взять полученный результат с противоположным знаком:

∫

= −

res

[

f (z), z

+res

[

(z), z

= 1 1+ 2.

2πi

(

)

1 ]

]

z +1 z

Пример 11.9 ([3], № 4.129).

C∫

= e

z ln a

), где а > 0,

2πi

az sin πz

а С – проходимая снизу вверх прямая х = α, 0 < α <1 .

Решение.

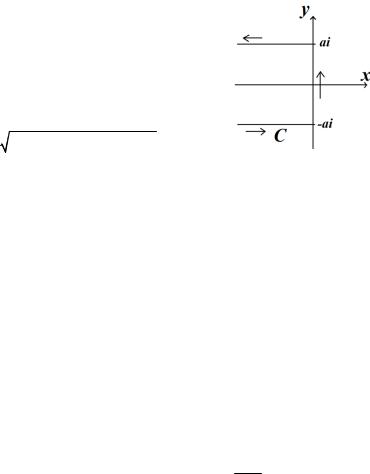
Рассмотрим контур γ,

пред-

ставленный на рис. 11.4. Внутри контура

функция

f (z) =

имеет единствен-

az sin πz

ную особую точку z = 1 – полюс первого

порядка. Вычет в этой точке вычислим по

формуле

Полагая

φ(z) =

ψ'

ψ( z ) = sin πz ,

ψ'( z ) = πcosπz ,

φ(1)

Рис. 11.4

res[ f (z),1] =

−1

ψ'(1)

aπ

Таким образом,

∫γ

= −

2πi

az sin πz

aπ

С другой стороны, этот интеграл равен сумме четырех интегралов по четырем сторонам прямоугольника, образующего контур γ. Рассмотрим каждый из них. Интеграл по нижнему горизонтально-

165

1+α

му отрезку z = x −iβ равен

∫α

. Оценим его

2πi

e( x−iβ)ln a sin π(x −iβ)

значение по модулю при β→+∞ :

1+α

∫α

≤

2πi

e(x−iβ)ln a (sin πx cos πiβ−cos πxsin πiβ)

1+α

≤

∫α

0 ,

2π

ex ln a sin2 πx ch2πβ+cos2 πx sh2πβ

так как под корнем в знаменателе экспоненциально растущая с ростом β функция. Аналогично оценивается интеграл по верхнему горизонтальному отрезку. Рассмотрим интегралы по вертикальным прямым. Обозначим вычисляемый интеграл:

C∫

= I .

2πi

az sin πz

Интеграл по левой вертикальной прямой (где z = α + iy ) равен

1 −β

idy

→

1 −∞

idy

= −I;

∫β

β→+∞

+∞∫

2πi

e(α+iy)ln a sin π(α+iy)

2πi

e(α+iy)ln a sin(πα+πiy)

интеграл по правой вертикальной прямой ( z = 1 + α + iy ) равен

1 β

idy

−∫β

2πi

eln ae(α+iy)ln a sin π(1+α +iy)

idy

= −

→

−

2πi eln a

−∫β e(α+iy)ln a sin (πα + πiy) при β→+∞

Получаем равенство

−I −

= −

I =

aπ

π(a +1)

Пример 11.10 ([3], № 4.130).

C∫

ez dz

, где контур интегриро-

2πi

cos z

вания С указан на рис. 11.5.

Решение. Контур С сделаем замкнутым, проведя через точку z = n (n – целое отрицательное число) вертикальный отрезок. Можно

166

показать, что интеграл по этому отрезку при

n →−∞ стремится к нулю, потому что при n →−∞

en+iy idy

−∫a

≤

cos(n +iy)

≤en ∫

→0.

cos

n ch

−a

y +sin

Тогда интеграл равен сумме вычетов в изо-

Рис. 11.5

лированных особых точках подынтеграль-

ной функции. Это будут точки

cos z = 0 zk

+ πk

(k = −1, −2,...) ,

+πk

res[ f (z), zk ]

= (−1)

k +1

−cos πk

−sin

πk

(k = −1, −2,...) ,

−∞

∞

1 e

= −∑(−1)k e

+πk

= −e

∑e−πk (−1)k .

2πi C∫ cos z

k =−1

k =1

Под знаком суммы стоит бесконечно убывающая геометрическая прогрессия со знаменателем q = −e−π и первым членом

a1 = −e−π . По формуле суммы прогрессии S = 1a−1q получим, что

∞

−e

−π

∑(−1)k e−πk =

= −

1+e

−π

k =1

Таким образом,

ez dz

∫

= −e

2 −

2πi

1+e

C cos z

167

Вычисление определенных интегралов

Интегралы типа ∫02π R(sinφ,cosφ)dφ, где R (sin φ, cos φ) – ра-

циональная функция переменных sin φ, cos φ,					вычисляются пере-
ходом к комплексной переменной			z = eiφ и		интегрированием в
комплексной плоскости по контуру		z		=1 (см. п.11.1).

Пример 11.11 ([3], № 4.131).
2π	dφ
∫0		(a >1) .
	a +cos φ

Решение. Вводим комплексную переменную z =eiφ , dz = ieiφdφ,

откуда dφ = dz

. По формуле Эйлера

eiφ +e−iφ

z + z−1

cosφ =

2π

dφ

∫0

= ∫

= i

∫

a +cos φ

z + z

−1

z2 +2az +1

|z|=1 iz a +

|z|=1

Знаменатель подынтегральной функции обращается в нуль в

точках	z		= −a ±	a2 −1 . При a >1 из этих двух точек только
	1,2
точка	z	= −a + a2		−1 попадает внутрь контура интегрирования
	1

z =1 (единичная окружность с центром в начале координат), так как, по теореме Виета, произведение z1z2 =1 (т.е. если один корень

внутри единичной окружности, то другой – вне ее). В этой точке функция имеет полюс первого порядка, так как квадратный трех-

член разлагается на множители z2 +2az +1 = ( z − z						)(z − z	2	) . Для
					1		2
вычисления интеграла найдем вычет в точке					z = −a + a2 −1 по
формуле (10.2):					1
формуле (10.2):		1
res[ f (z), z	] = lim	1			(z − z	) =
res[ f (z), z	] = lim	)(z − z		)	(z − z	) =
1	z→z1 (z − z	)(z − z	2	)	1
	1		2

168

− z2

−a + a2 −1 −(−a − a2

−1) 2 a2 −1

Искомый интеграл равен:

2π

dφ

2π

∫0

= 2πi i

a +cosφ

a2 −1

2π

dφ

Пример 11.12

([3], № 4.134).

∫

( a

– ком-

1−2a cosφ+a2

плексное число и a ≠ ±1).

Решение. Как и в предыдущем примере, введем комплексную переменную z = eiφ :

2π

dφ

∫

=−

1−2acosφ+a2

z +z−1

1+a2

=1 iz 1−2a

+a2

=1 z

−

z +1

Корни квадратного трехчлена, стоящего в знаменателе:

z	= a2 +1	± a2 −1 ;	z = a ; z	2	= 1 .
1,2	2a	2a	1	2	a
	2a	2a			a

При a <1 внутри контура интегрирования находится точка z1 , а z2 – вне контура. Вычет в точке z1 (полюс первого порядка) равен

res[ f (z), z

] = lim

f (z) (z − z

) = lim

(z − z1 )

)

z→z1

(z − z

)(z − z

(z1 − z2 )

a −

a2 −1

Поэтому искомый интеграл равен

2π

dφ

∫

= −

∫

1− 2a cos φ+ a

=1 ( z − z1 )( z − z2 )

= −

2πi

2π

a2 −1

1− a2

169

В случае, если

> 1, внутрь контура попадает точка

z2 =

res f

, z

= lim

−z

(

)

(z −z1 )(z −z2 ) (

z2 −z1

−a2

z→z2

2 )

−a

Интеграл равен

2π

. Если же

a = ±1 , то

a2 −1

2π

dφ

2π

dφ

∫

= ∫

1−2a cosφ+a

2(1 ±cosφ)

и подынтегральная функция имеет в точке φ = 0

(или φ = π

соот-

ветственно)

особенность типа

т.е. интеграл не существует да-

же в смысле главного значения. Наконец, если

= 1,

но

a ≠ ±1,

т.е. a = eiα(α ≠ 0,π,2π) , то

2π

eiφdφ

−

∫

= − a

∫0

(z − z1 )(z − z2 )

(eiφ −eiα )(eiφ −e−iα )

2π

dφ

= −

∫0 (1 −ei(α−φ) )(eiφ −e−iα ) .

В точках φ = ±α подынтегральная функция имеет особенность типа φ1−α , т.е. главное значение интеграла существует (оно в этом случае равно нулю).

Рекомендуемый перечень задач для решения в аудитории:

[3], № 4.115, 4.117, 4.120, 4.121, 4.122, 4.131.

Резерв:

[3], № 4.123, 4.128, 4.129, 4.130, 4.134.

Для самостоятельной работы дома:

[3], № 4.118, 4.119, 4.124, 4.132.

На усмотрение преподавателя: [3], № 4.127, 4.133.

170

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 2517 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
04.06.20152.52 Mб74методы оптимизации шпоры.doc
#
22.08.201925.59 Кб6Метрология.docx
#
04.06.20156.71 Mб475Механика 9 кл 2009 в2.doc
#
05.06.201586.64 Кб9мжд. право.docx
#
04.06.20151.11 Mб42мировая экономика_лекции_.doc
#
05.06.20153.91 Mб1470Михайлов ТФКП практикум2013.pdf
#
05.06.2015979.95 Кб23Михеенко Макроэкономика.pdf
#
05.06.20153.62 Mб34Михеенко Микроэкономика.pdf
#
11.11.2019128.33 Кб7МО_ИСО 10019-2007 - Рук-во по выбору консультан...rtf
#
09.08.2019169.47 Кб16моделир.doc
#
05.06.2015439.43 Кб102Моднейший справочник по ТИ.pdf