
- •1. Двойные интегралы
- •Задача об объёме цилиндрического бруса
- •Условия существования двойного интеграла
- •1.3. Свойства двойных интегралов
- •Вычисление двойных интегралов
- •3. Замена переменных в двойном интеграле
- •4. Тройной интеграл
- •4.1. Определение и условия существования тройного интеграла
- •4.2. Вычисление тройного интеграла в декартовых координатах
- •5. Вычисление тройного интеграла в криволинейных системах координат
- •5.1. Замена переменных в тройном интеграле
- •5.2. Поверхности второго порядка
- •5.3. Примеры
- •Объём тела удобно вычислять тройным интегралом:
- •6. Криволинейный интеграл первого рода
- •7. Поверхностный интеграл первого рода
- •Литература
5.3. Примеры
Пример 5.1. Вычислить интеграл в цилиндрических координатах:
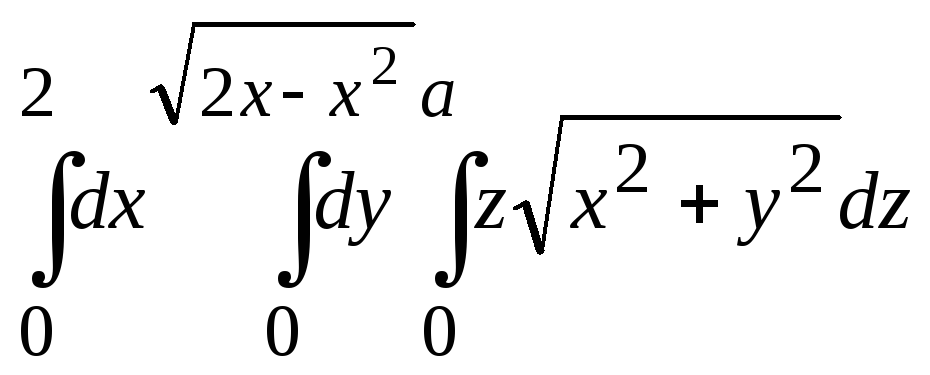 .
.
Решение.
Восстановим область интегрирования
![]() по известным пределам интегрирования:
по известным пределам интегрирования:
![]()
Область
![]() (проекция области
(проекция области![]() на плоскость
на плоскость![]() )
расположена в первой четверти и ограничена
прямой
)
расположена в первой четверти и ограничена
прямой![]() и линией
и линией![]() .
.
Преобразуем последнее выражение. После возведения в квадрат получим
![]() , (5.3)
, (5.3)
а после простых преобразований будем иметь
![]() .
.
Это
уравнение окружности радиусом
![]() ,
центр которой смещён в положительную
сторону по оси
,
центр которой смещён в положительную
сторону по оси![]() на радиус. Границей области
на радиус. Границей области![]() является правая половина этой окружности.
является правая половина этой окружности.
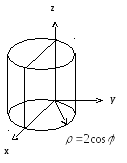
Рис. 5.9
Уравнение окружности в цилиндрических координатах получим, подставив в (5.3) соотношения:
![]() ;
;
![]() ;
;
![]() или
или
![]() .
.
Точка
пробегает правую половину окружности
при изменении угла
![]() от 0 до
от 0 до![]() ;
подынтегральное выражение в цилиндрических
координатах имеет вид:
;
подынтегральное выражение в цилиндрических
координатах имеет вид:
![]() .
.
Тело
![]() изображено на рис. 5.9.
изображено на рис. 5.9.
Интеграл вычисляем в цилиндрических координатах:
![]()
![]()
![]()
![]() .
.
Пример 5.2. Вычислить интеграл:
![]() ,
,
если
область интегрирования
![]() ограничена сферой
ограничена сферой
![]() .
.
Уравнение сферы простыми преобразованиями приводится к виду
![]() .
.
Это
– сфера радиусом
![]() ,
смещенная вверх по оси
,
смещенная вверх по оси![]() на радиус (рис. 5.10).
на радиус (рис. 5.10).
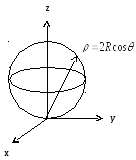
Рис. 5.10
Решение. Вычисления проведём в сферических координатах. Уравнение границы области преобразуем, подставив в уравнение сферы соотношения
![]() .
.
![]() ,
или
,
или
![]() .
.
Подставив те же соотношения в подынтегральное выражение, получим
![]() .
.
Области изменения переменных:
![]() .
.
Интеграл в сферических координатах легко вычислить:
![]()
![]()
![]() .
.
Объём тела удобно вычислять тройным интегралом:
 .
.
В цилиндрических координатах интеграл принимает вид:
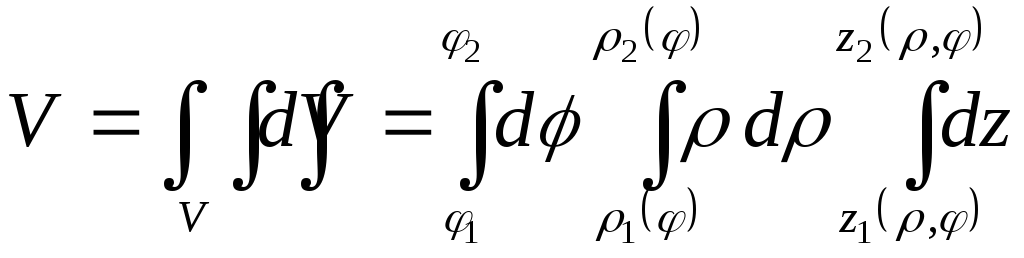 .
.
В сферических координатах:
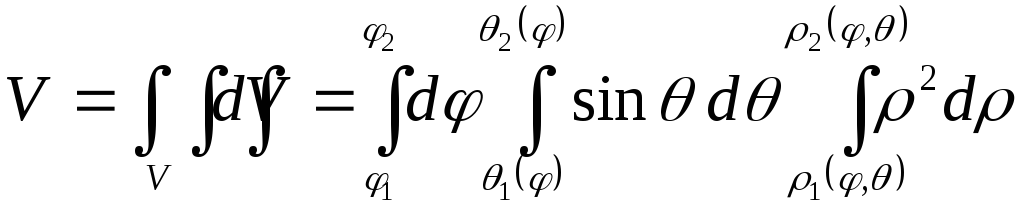 .
.
Пример 5.3. Вычислить объём тела, ограниченного сферой
![]() и
конусом
и
конусом
![]() (рис.
5.11).
(рис.
5.11).
Решение. Уравнение сферы простыми преобразованиями приводится к виду:
![]() .
.
В сферических координатах уравнение сферы
![]() .
.
Уравнение конуса
![]() .
.
Области изменения переменных
![]() .
.


Рис. 5.11
Искомый объём вычислим в сферических координатах:
![]()
![]()
![]() .
.
Вычисление интеграла в данной задаче можно произвести в цилиндрических координатах.
Преобразуем уравнения сферы и конуса, подставив в них соотношения
![]() .
.
Уравнение верхней половины сферы
![]() .
.
Уравнение верхней половины конуса
![]() .
.
Проекция
объёма
![]() на плоскость
на плоскость![]()
круг радиусом
круг радиусом
![]() .
Области
изменения переменных
.
Области
изменения переменных
![]() .
.
Эти данные позволяют расставить пределы в повторных интегралах и вычислить искомый объём:
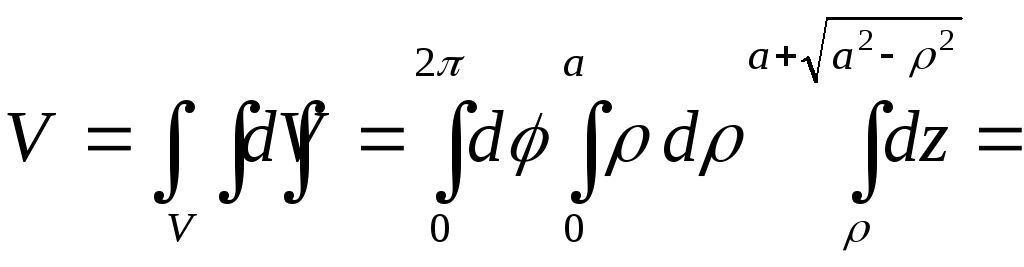
![]()
 .
.
Пример 5.4. Вычислить объём тела Вивиани, образованного пересечением сферы
![]()
и цилиндра с вертикальными образующими
![]() .
.
(На рис. 5.12 приведено изображение только верхней половины тела Вивиани.)

Рис. 5.12
Решение. Вычислим интеграл в цилиндрических координатах. Преобразуем уравнения сферы и цилиндра, подставив в них соотношения
![]() .
.
Уравнение сферы
![]() .
.
Уравнение цилиндра
![]() .
.
Вычислим объём четверти тела Вивиани, лежащей в первом октанте, и результат умножим на 4, что возможно, так как тело симметрично.
Области изменения переменных
![]() .
.
Вычисление тройного интеграла сведется к вычислению трех повторных интегралов, пределы интегрирования в которых соответствуют данным, приведенным выше:
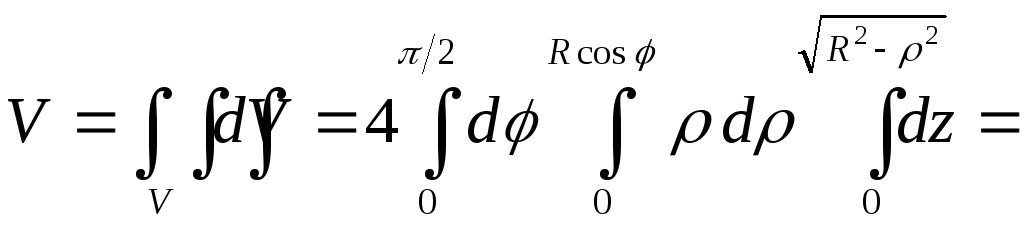
![]()

![]()
![]()
![]() .
.
Решить самостоятельно: [1] № 3590, 3592, 3593.
