4. Тройной интеграл

4.1. Определение и условия существования тройного интеграла

При построении определения тройного интеграла основную роль играет понятие объёма. Условие существования объёма для трёхмерного тела состоит в том, чтобы ограничивающие его поверхности описывались кусочно-гладкими функциями. Только такие поверхности мы и будем рассматривать, что обеспечит существование объёмов во всех нужных нам случаях.

Пусть в некоторой пространственной области задана функция. Этой функцией может быть задана, например, плотность распределенных в объёме масс. Будем решать задачу определения массы, заключенной в объёме.

Разобьём область с помощью сети поверхностей на части. (Для объёмов этих частей сохраним обозначения). В каждом элементефиксируем произвольную точку, значение функции в этой точкеумножим на объёми составим интегральную сумму:

.

Определение. Конечный предел интегральной суммыпри стремлении к нулю наибольшего из диаметров частичных объёмови , если он существует для любого разбиения объёманаи не зависит от выбора точек, называется тройным интегралом от функциив области.

Интеграл обозначается символом:

.

Конечный предел подобного вида может существовать только для ограниченной функции.

Для решения вопроса о существовании тройного интеграла вводятся в рассмотрение, кроме интегральной суммы , еще нижняя и верхняя суммы Дарбу:

и ,

где

.

Для существования интеграла необходимо и достаточно, чтобы

или ,

где есть колебание функциив области.

Из этих условий следует, что всякая непрерывная функция интегрируема. Можно несколько расширить эти условия, а именно: интегрируема всякая ограниченная функция, все разрывы которой лежат на конечном числе кусочно-гладких поверхностей.

Свойства тройных интегралов полностью совпадают со свойствами двойных, поэтому не будем на них останавливаться.

4.2. Вычисление тройного интеграла в декартовых координатах

Область , в которой вычисляется тройной интеграл, есть замкнутая пространственная область. Снизу и сверху она ограничена поверхностями, определяемыми уравнениямии, а с боков – цилиндрической поверхностью с образующими, параллельными оси (рис. 4.1).

Переменные иизменяются в области, которая является проекцией на плоскостьпространственной области.

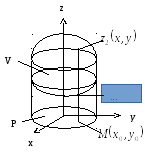
Рис. 4.1

Элемент объёма в прямоугольной декартовой системе координат

.

Тройной интеграл можно представить повторным интегралом:

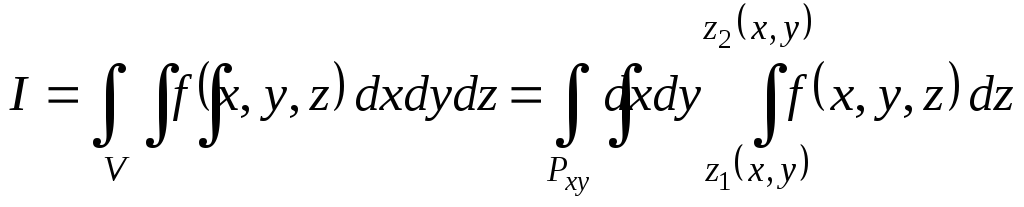. (4.1)

Функция предполагается непрерывной в замкнутой области, что обеспечивает существование исходного тройного интеграла, двойного интеграла по областии внутреннего интеграла

.

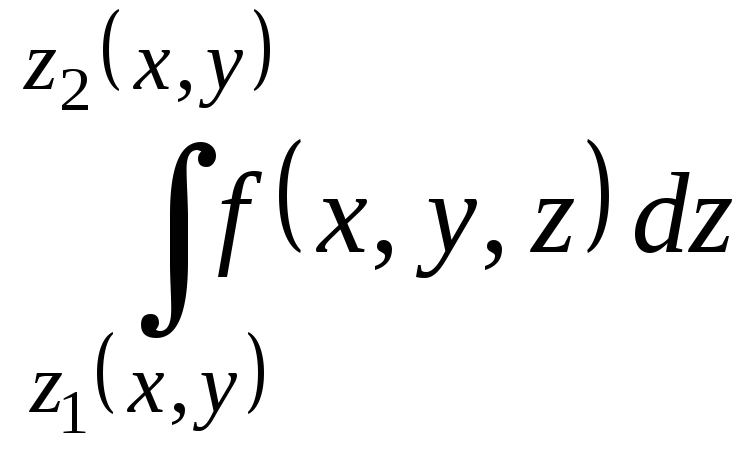При вычислении внутреннего интеграла переменные исчитаются постоянными и единственной переменной величиной является. Линию интегрирования в этом случае можно представить перпендикуляром, проведенным из произвольной фиксированной точки области, а сама областьдолжна быть такой, чтобы перпендикуляр пересекал ограничивающие её поверхности только в двух точках.

(В более сложных случаях область может быть разбита на части, и интегрирование в каждой части проведено отдельно.)

Нижний предел интеграла определяется как координата точки входа перпендикуляра в область  , а верхний предел – как координата точки выхода . Каждой произвольно фиксированной точке областивнутренний интеграл ставит в соответствие некоторое число и тем самым определяет в областинекоторую функцию. Подставив её в двойной интеграл в формуле (4.1), сведём вычисление тройного интеграла к вычислению двойного интеграла

.

Если область ограничена непрерывными кривымии, и проецируется но осьв отрезок, то двойной интеграл можно вычислить повторным интегрированием:

.

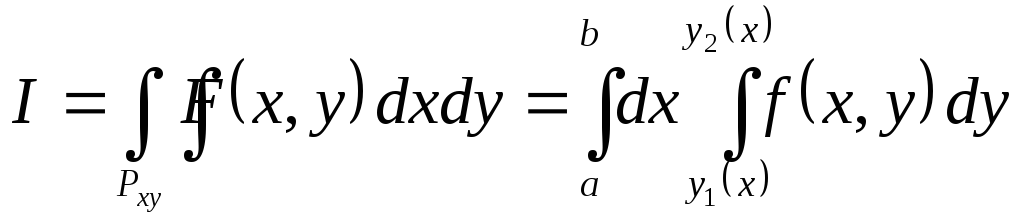Тем самым вычисление тройного интеграла может быть сведено к трём последовательно вычисляемым интегралам:

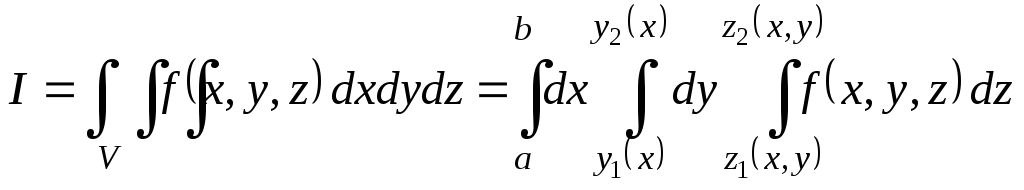. (4.2)

Порядок интегрирования может быть изменён, а так как в формуле три переменных и, то число способов вычисления тройного интеграла оказывается равным числу перестановок трёх элементов, то есть шести.

Возможен несколько иной взгляд на переход от тройного интеграла к повторному. Пусть тело расположено между плоскостямии, перпендикулярными к оси, а в сечении телаплоскостьюполучается фигура. (Плоскость перпендикулярна к оси, а произвольная точка, удовлетворяющая условию .) Тройной интеграл в этом случае можно представить так:

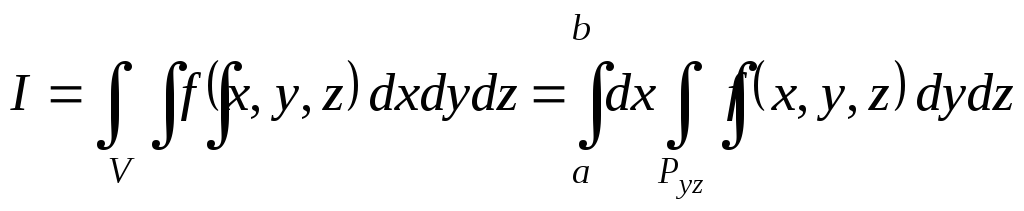. (4.3)

Изменение порядка интегрирования в повторном интеграле здесь также возможно; двойной интеграл вычисляется обычным образом.

Если функция , то тройной интеграл оказывается равным объёму тела:

. (4.4)

Вычисление объёма тела с помощью тройного интеграла во многих случаях оказывается более наглядным и эффективным, чем с помощью двойного интеграла.

Пример 4.1 Вычислить интеграл:

,

где  пирамида, гранями которой являются координатныеплоскостии плоскость (рис. 4.2).

Решение.

.

Обоснуем расстановку пределов.

Пирамида ограничена снизу плоскостью , сверху – плоскостью, поэтому переменнаяво внутреннем интеграле может изменяться отна основании пирамиды дона наклонной плоскости.

Проекцией области на плоскость является прямоуголь-ный треугольник, катеты которого лежат на осяхи, а гипотенуза есть линия пересечения плоскостии плоскости. Уравнение гипотенузы:.

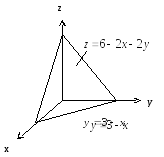
Рис. 4.2

Область проецируется на осьв отрезок, что даёт пределы внешнего интеграла. Переменнаяпри любом фиксированномможет изменяться от значенияна катете до значенияна гипотенузе треугольника. Именно такими оказываются пределы интеграла по переменной.

Вычислим последовательно интегралы, начиная с последнего:

.

.

Пример 4.2. Вычислить интеграл:

,

г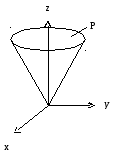де объёмограничен конусоми плоскостью(рис. 4.3).

Рис. 4.3

Решение. Перейдём к повторному интегралу:

.

Здесь фигура получена сечением конуса плоскостью, проходящей на высотеперпендикулярно к оси. Это круг радиусом , а двойной интеграл, представляющий его площадь,

,

откуда следует

.

Пример 4.3 Вычислить интеграл:

,

где объём  общая часть двух сфер (рис. 4.4):

и .

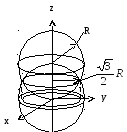
Рис. 4.4

Решение. Преобразуем уравнение второй сферы:

,

вторая сфера смещена вверх по оси на радиус, а центр первой сферы – в начале координат.

Линия пересечения двух сфер лежит на плоскости .

Сечения тела плоскостями, параллельными плоскости, суть круги, радиусыкоторых зависят от переменной.

Если , тои площадь соответствующего круга.

Если же , тои площадь круга в сечении верхней половины тела .

Объём тела будем вычислять как сумму двух повторных интегралов, гдеи площади кругов, образованных в сечениях горизонтальными плоскостями в нижней и верхней половинах тела :

.

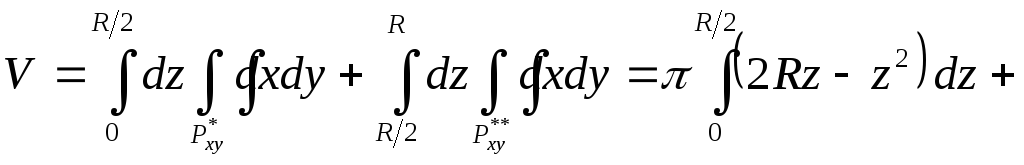
Решить самостоятельно: [1] № 3610, 3611, 3614, 3615.