Задача 1

Строительная фирма организовала выпуск деревянных домов двух видов А и В. Для производства первой партии домов фирма приобрела брус - на $100 тыс., вагонку – на $150 тыс. и обрезную доску – на $160 тыс. На постройку дома вида А требуется брус – на $1 тыс. и вагонка – на $3 тыс., а на постройку дома вида В – брус на $2 тыс., вагонка – на $1 тыс. и обрезная доска – на $4 тыс.

Фирма планирует продажу домов вида А по цене $10 тыс., а вида В – по цене $30 тыс.

1. Определить оптимальный план выпуска домов и прибыль от их реализации.

2. Определить наличие излишков приобретенных стройматериалов. Оценить, какую сумму можно дополнительно выручить за счет продажи излишков стройматериалов (по закупочным ценам).

3. Фирма решила не продавать излишки стройматериалов, а на имеющиеся финансовые резервы в размере $10 тыс. закупить дополнительно необходимые стройматериалы. Определить, какой вид стройматериалов целесообразно дополнительно закупить и какую дополнительную прибыль можно за счет этого получить.

Издержками считать стоимость стройматериалов.

Решение

1) Представим данные в табличной форме:

	А	В	Стоимость $тыс.
Брус	1	2	100
Вагонка	3	1	150
Обрезная доска	0	4	160
Цена дома $ тыс.	10	30
	х1	х2

Формализуем задачу:

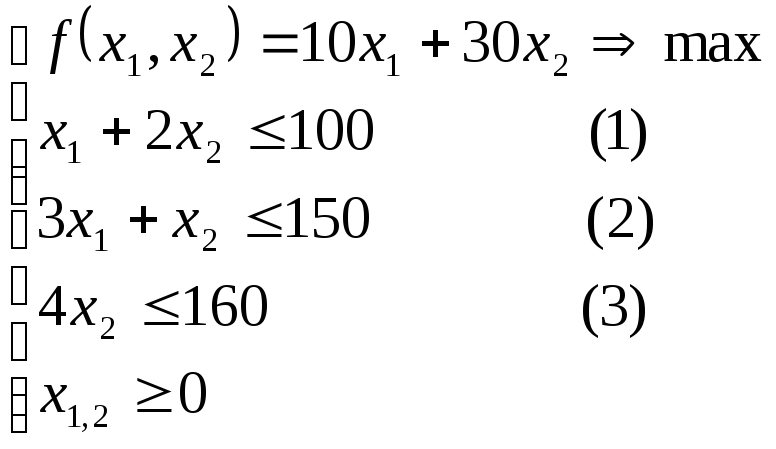
Изобразим допустимое множество и линию уровня целевой функции – см. рис. 4.16.

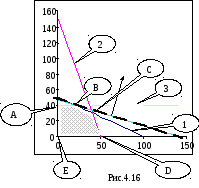
Как видно из рис. 4.16, максимум целевой функции достигается в точке В, в которой пересекаются ограничения 1 и 3. Найдем эту точку:

.

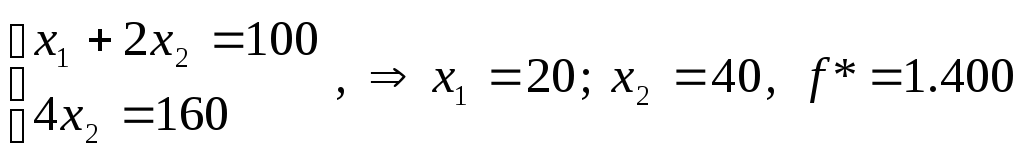Таким образом, оптимальный план постройки домов: (20; 40). При этом фирма получит доход в размере $1.400 тыс., а прибыль составит 1.400 – 100 – 150 – 160 = 990 (тыс. долларов).

2. Из рис. 4.16 видно, что ограничение 2 не активно. Это значит, что вагонка закуплена в избытке и ее количество можно было бы сократить без изменения оптимального решения и значения целевой функции (дохода). Допустим, что фирма имеет возможность продать излишки по закупочной цене. Определим объем излишков (в тыс. долларов). Пусть мы оставляем вагонки для постройки домов на 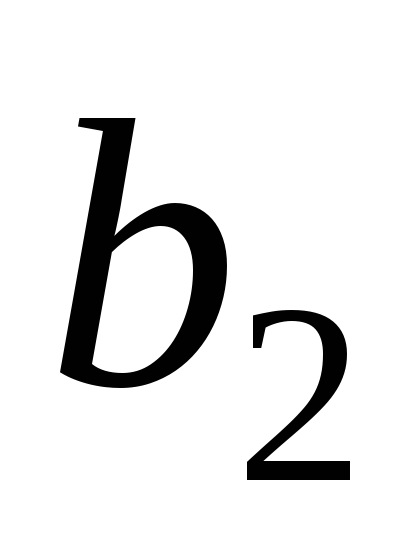тыс. долларов. Тогда вместо 2 имеет место неравенство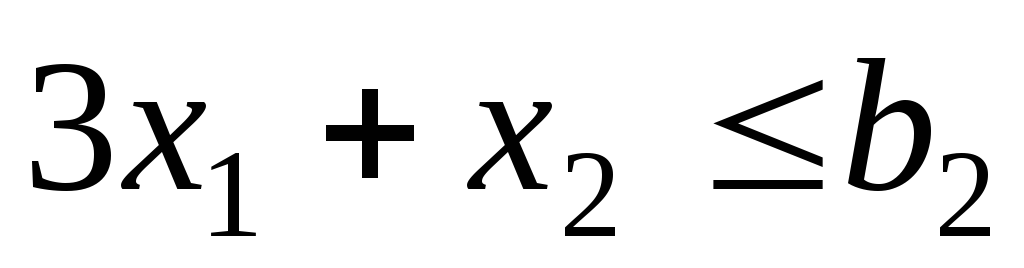. Соответствующая граничная линия, очевидно, будет параллельна линии 2. Для того, чтобы оптимальная точка осталась на месте, нужно, чтобы линия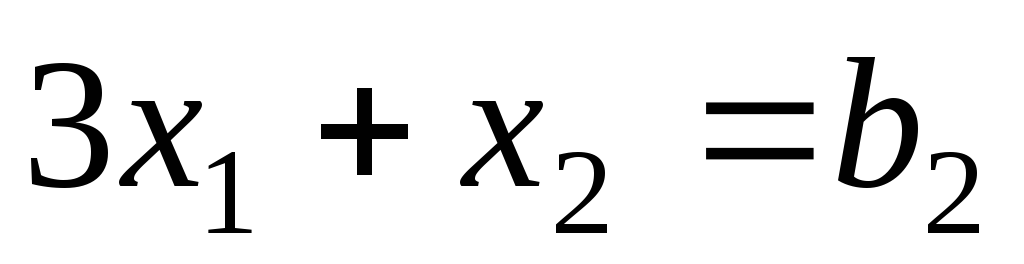была правее точки В или проходила через нее. В случае прохождения данной линии через точку В мы будем иметь минимальное значение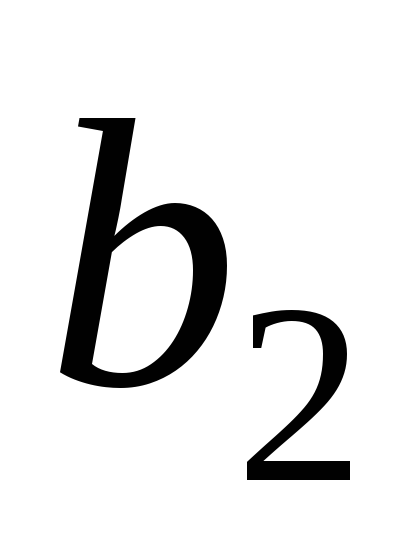и, таким образом, максимальную дополнительную выручку от продажи излишков:.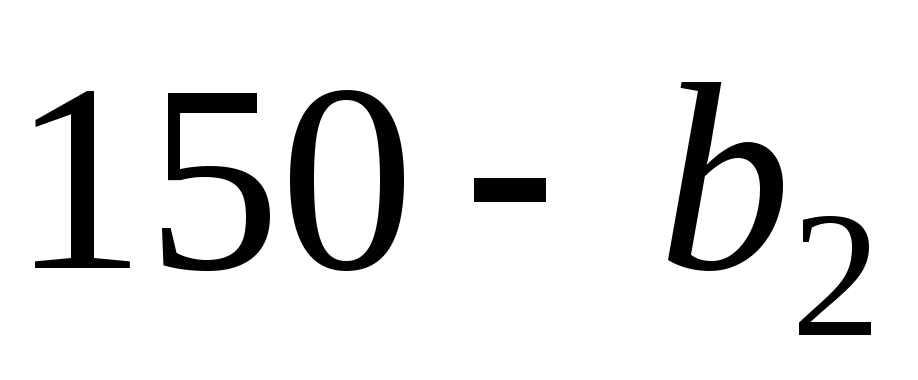

Итак, имеем: , и дополнительная выручка от продажи излишков равна 150 – 100 = 50 (тыс. долларов).

2. Пусть фирма имеет резерв финансовых средств на дополнительную закупку стройматериалов в размере $10 тыс. Оценим, какой вид стройматериалов целесообразно закупить.

Поскольку все константы измеряются в единых единицах (тыс. долларов), то ответ на этот вопрос непосредственно дадут множители Лагранжа (двойственные переменные) . Итак, перейдем к двойственной задаче:

.

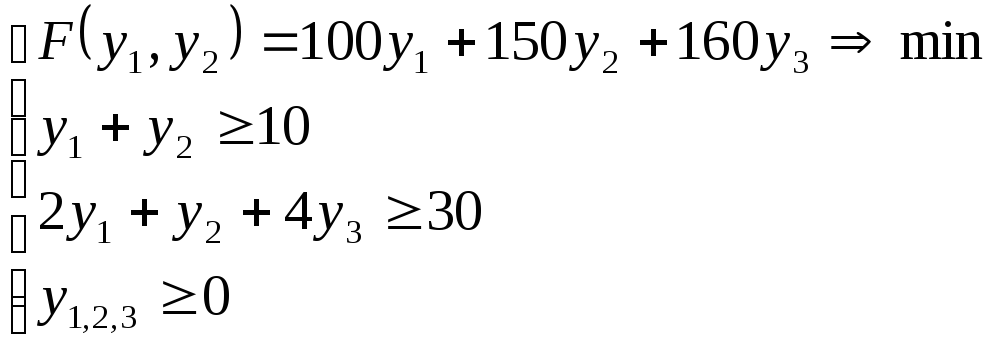Так как в оптимальной точке прямой задачи ограничение 2 не активно, то в оптимальной точке двойственной задачи , а так как, то оба функциональных ограничения должны выполняться как равенства:

.

Отсюда видно, что выгоднее всего дополнительно закупить брус (). Посмотрим, до каких размеров можно увеличивать запас бруса. Очевидно, значениесохранится, по крайней мере, до тех пор, пока не изменится базис, т.е. пока при передвижении прямойпараллельно самой себе активным не станет ограничение 2. Предельное значениеможно получить, подставив в условиеточку С, в которой пересекаются ограничения 2 и 3:

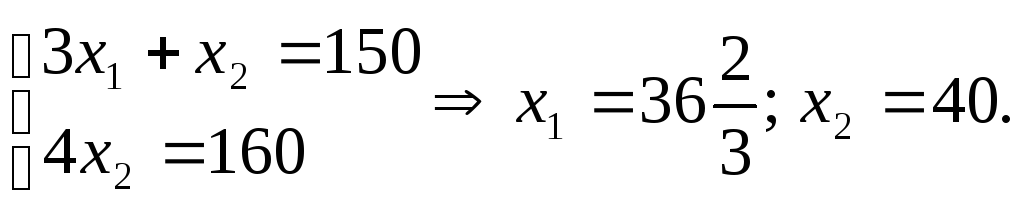
В этой точке

Таким образом, сохранит свое значение при увеличениина 116²/₃ –100 = = 16²/₃ (тыс. долларов), что больше имеющегося резерва финансовых средств. Таким образом, $10 тыс. целесообразно использовать полностью для дополнительной закупки бруса. При этом оптимальный доход увеличится на (тыс. долларов), а прибыль на 100 – 10 = 90 (тыс. долларов).

Методом, подобным описанному можно проводить более глубокий анализ зависимости оптимального значения целевой функции от констант ограничений. Покажем как это делается на примере разобранной задачи для зависимости , где считаем, что константа первого ограничения является параметром, а все остальные параметры фиксированы и равны тем, что даны в условии задачи.

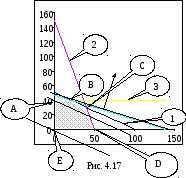
Как уже отмечалось, при изменении граница 1 будет параллельно перемещаться. На рис. 4.17 изображены критические положения этой границы, когда происходит смена базиса.

Очевидно, при допустимое множество состоит из одной точки Е и.

При перемещении границы до пересечения с точкой А оптимальное решение будет в точке и оптимальное значение целевой функции равно. В точке А.

При дальнейшем перемещении границы до точки С() оптимальное решение будет лежать на границе 3:

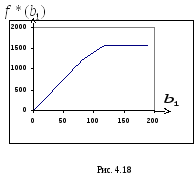
При дальнейшем перемещении границы первое ограничение перестает быть активным и целевая функция не изменяется: - см. рис. 4.18.

Если фирма может управлять ценами на произведенную продукцию, может иметь смысл проводить анализ чувствительности оптимального значения целевой функции к коэффициентам . Проведем для примера анализ зависимости.

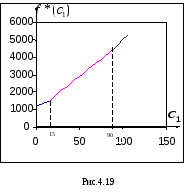
Итак, имеем: ,. Для построения графикасоставим таблицу:

Оптималь-ная точка / отрезок		Координаты точки/ уравнение отрезка		Градиенты активных ограничений		Градиент оптимизирующей целевой функции
	A		(0;40)		(-1;0), (0;4)		-		-	-
	AB				(0;4)		(0;30)		0	1200
	B		(20;40)		(0;4), (1;2)				(0;15)
	BC				(1;2)		(15;30)		15	1500
	C		(40;30)		(1;2), (3;1)				(15;90)
	CD				(3;1)		(90;30)		90	4500
	D		(50;0)		(3;1), (0;-1)				(90;)
	DE				(0;-1)		-		-	-
	E		(0;0)		(0;-1), (-1;0)		-		-	-
	EA				(-1;0)		-		-	-

Заметим, что если активно одно ограничение (отрезок), то градиент целевой функции должен быть пропорционален градиенту соответствующего ограничения.

График изображен на рис. 4.19.