Теорема о существовании решений

Задача линейного программирования вида (4.4) или (4.5) имеет решение тогда и только тогда, когда допустимые множества прямой и двойственной задачи оба не пусты.

Действительно, если в прямой задаче допустимое множество пусто, то условие Куна-Таккера не выполняется ни при каких значениях х иу, а значит, и не может быть оптимума ни в одной из задач.

Обратно, если оба допустимых множества не пусты, то существуют допустимые точки и, причем для любых допустимых точекх иу:и, т.е. максимизируемая функцияограничена сверху, а минимизируемая () – снизу. Ввиду линейности функций и замкнутости допустимых множеств отсюда следует наличие глобальных оптимумов.

Теорема о совпадении оптимальных значений

Допустимые векторы х иуявляются решениями задач (4.4) и (4.5) тогда и только тогда, когда значения целевых функций обеих задач на этих векторах совпадают:.

Это утверждение непосредственно следует из неравенства (4.9) и условия задач (4.4) и (4.5) – требований максимизации и минимизации целевых функций.

Теорема о дополняющей нежесткости

Допустимые векторы х иуявляются решениями задач (4.4) и (4.5) тогда и только тогда, когда они удовлетворяют условиям дополняющей нежесткости:

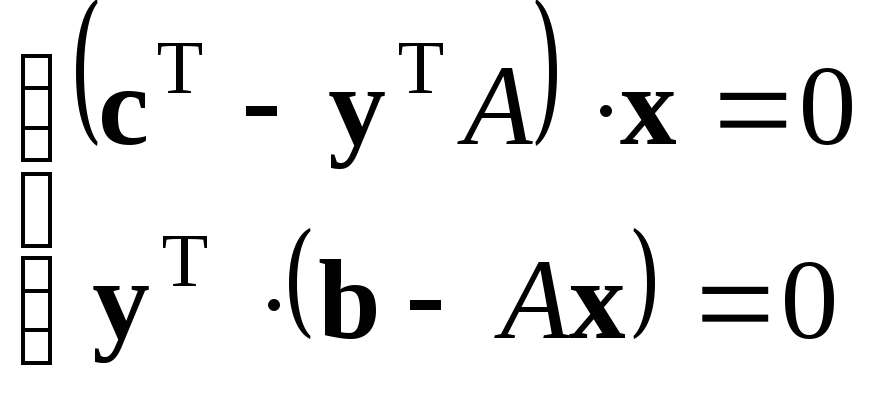. (4.11)

Это утверждения вытекает из предыдущей теоремы и системы условий (4.10).

Ввиду практической важности последней теоремы для решения задач графическим способом рассмотрим условия (4.8) подробнее. Для этого представим их в скалярной форме:

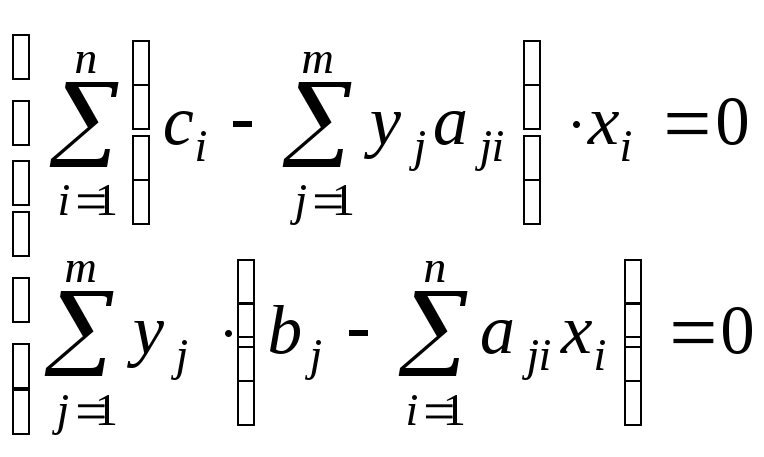(4.12)

Поскольку мы рассматриваем только допустимые точки, то и,а значит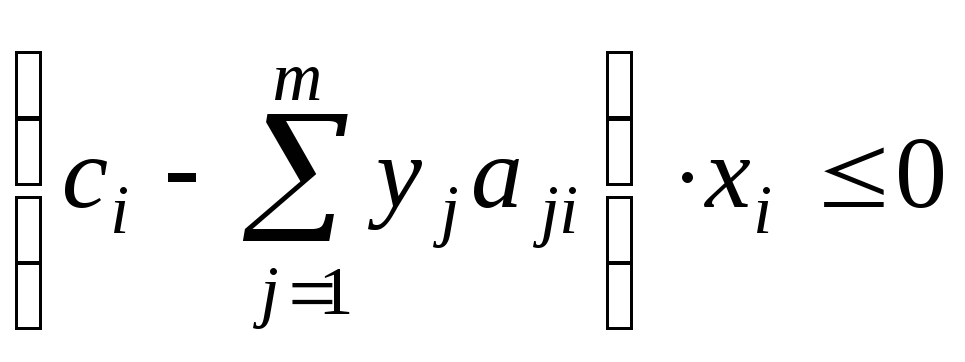,т.е. каждое слагаемое в первом неравенстве (4.12) неположительно. Однако сумма их равна нулю. Очевидно, это возможно только при равенстве нулю каждого слагаемого. Таким образом,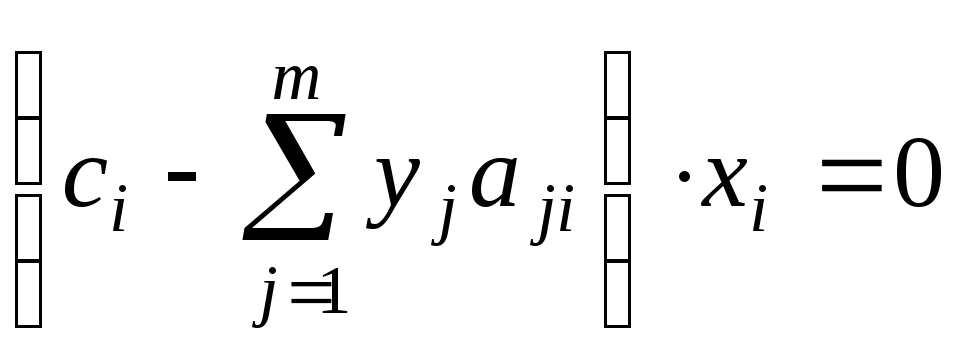,а это, в свою очередь, означает, что в каждом таком произведении хотя бы один из сомножителей равен нулю.

Иными словами, можно сказать, что если в оптимальной точке (прямой задачи) , то, или, что то же самое,, т.е. соответствующее ограничение в оптимальной точке двойственной задачи превращается в равенство (активно). И наоборот, если в оптимальной точке двойственной задачи, т.е. некоторое ограничение не активно, то соответствующая переменная в оптимальной точке прямой задаче равна нулю:.

Аналогичные рассуждения справедливы относительно второго равенства из (4.12) с той лишь разницей, что там все сомножители неотрицательны.

Суммируя сказанное, теорему о дополняющей нежесткости можно сформулировать следующим образом:

1⁰ Если в оптимальной точке прямой задачи некоторое ограничение не активно (неравенство выполняется строго), то в оптимальной точке двойственной задачи соответствующая переменная равна нулю.

2⁰ Если в прямой задаче некоторая переменная не равна нулю (строго положительна), то в оптимальной точке двойственной задачи соответствующее ограничение обращается в равенство (активно).

Напомним, что понятия прямой и двойственной задач относительны: любую из взаимно двойственных задач можно считать прямой, тогда другая будет двойственной к ней.

Двойственные задачи допускают следующую экономическую интерпретацию.

Будем называть прямой задачей задачу на максимум вида (4.4), а двойственной – задачу на минимум вида (4.5).