
get_2 физика
.pdf
ванку равен отношению энергии, затраченной на деформацию болванки, ко всей затраченной энергии E1 :
η = E E1 , или η = (E1 − E2 ) E1 . |
(4) |
|||
Подставляя в выражение (4) E2 |
из (3), получим выражение |
|||
для КПД: |
|
|
|
|
η = |
m2 |
|
. |
|
m + m |
2 |
|
||
1 |
|
|
||
После подстановки числовых значений найдем: η = 92,6 %.
Ответ: E1 = 400 Дж, E2 = 29,6 Дж, E = 370 Дж, η = 92,6 %.
Пример 12. Тело массой 1,0 кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного
телом, от времени задана уравнением s = 2t 2 + 4t + 1. Определить работу силы за 10 секунд с начала ее действия и зависимость кинетической энергии от времени.
Дано:
m = 1,0 кг,
s = 2t 2 + 4t + 1.
Найти: A , Eк = f (t).
Решение. Работа, совершаемая силой, выражается через ин-
теграл [4.4] A = ò F cos αds (1).
Сила, действующая на тело, по второму закону Ньютона [2.1]
равна F = ma или F = m |
d 2 s |
(2). Мгновенное значение ускорения |
|
dt 2 |
|||
|
|
определяется первой производной от скорости по времени или второй производной от пути по времени [1.10]. В соответствии с этим находим:
υ = |
ds |
|
= 4t + 4 , |
(3) |
|||
dt |
|||||||
|
|
|
|
|
|||
a = |
d 2 s |
= 4,0 м/с2. |
(4) |
||||
|
|||||||
|
|
dt 2 |
|
|
|
||
|
|
|
|
|
|
51 |
|

Тогда F = m |
d 2 s |
= 4m |
(5). Из выражения (3) определим ds : |
|
dt 2 |
||||
|
|
|
ds = (4t + 4)dt (6). Подставив (5) и (6) в выражение (1), учтя, что
cos α = 1 (направление силы совпадает с направлением перемещения), получим:
A = ò 4m(4t + 4)dt .
Из этого выражения определим работу, совершаемую силой за 10 с после начала ее действия:
10 |
ét 2 |
|
|
10 |
ù |
|
|||
|
10 |
|
|
||||||
A =16m ò |
(t +1)dt =16mê |
|
|
0 |
+t |
0 |
ú |
= |
|
2 |
|||||||||
0 |
ë |
|
|
|
|
û |
|
||
=16 ×1,0 × (0,5 ×100 +10) = 960 Дж.
Кинетическая энергия поступательно движущегося тела [4.11] определяется выражением:
Eк = mu2 / 2 . |
(7) |
Подставляя (3) в (7), получим: |
|
Eк = m(4t + 4)2 / 2 = m(16t 2 + 32t +16) / 2 = m(8t 2 |
+ 16t + 8) . |
Ответ: A = 960 Дж, Eк = m(8t 2 + 16t + 8) .
Пример 13. Радиус Земли равен 6370 км, ускорение свободного падения на поверхности Земли 9,81м/с2. Определить ее среднюю плотность.
Дано:
Rз = 6370 км = 6,37 ×106 м,
G = 6,67 ×10−11 м3/(кг×с2).
Найти:  r
r .
.
Решение. Сила, с которой тело массой m притягивается к Земле, выражается законом всемирного тяготения [3.1]:
F = G mM , (1) Rз2
52

где G – гравитационная постоянная, M – масса Земли, Rз – ра-
диус Земли.
Считая Землю шаром, выразим ее массу через объем (объем
шара) и среднюю плотность r : |
|
||
M =V r = |
4 |
pRз3 r . |
(2) |
|
|||
3 |
|
|
|
У поверхности Земли сила гравитационного взаимодействия |
|||
F сообщает телу массой m ускорение g |
(ускорение свободного |
||
падения), т.е. действует сила тяжести [3.2], тогда выражение (1) запишется в виде:
mg = G mM . Rз2
Исключая массу тела и подставляя массу Земли из соотношения (2), получим:
g = 4pGRз  r
r , 3
, 3
откуда получим искомое выражение для средней плотности Земли:
 r
r = 3g . 4pGRз
= 3g . 4pGRз
Подставляя числовые значения величин, находим:
|
3 × 9,81 |
3 |
r = |
|
= 5500 кг/м . |
4 × 6,67 ×10−11 × 6,37 ×106 |
Ответ:  r
r = 5500 кг/м3.
= 5500 кг/м3.
Пример 14. Какую скорость нужно сообщить ракете, чтобы она, стартовав с Земли, не вернулась на планету? Сопротивление атмосферы и движение Земли не учитывать.
Дано:
Rз = 6,37 ×106 м, g = 9,8 м/с2.
Найти: u0 .
53

Решение. С удалением ракеты от Земли будет увеличиваться ее потенциальная энергия и уменьшаться кинетическая. По закону сохранения механической энергии [4.12]:
Eк1 + Eп1 = Eк2 + Eп2 .
Так как кинетическая энергия тела, движущегося с некоторой скоростью [4.11] Eк = mu2 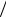 2 , а потенциальная энергия тела в поле тяготения [4.9] Eп = -Gm1m2
2 , а потенциальная энергия тела в поле тяготения [4.9] Eп = -Gm1m2 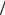 R , то получим выражение:
R , то получим выражение:
mu2 |
|
|
|
mM |
|
|
mu2 |
|
|
mM |
|
|
|||||
0 |
- G |
|
|
|
|
= |
|
|
|
|
- G |
|
|
|
или, после преобразований, |
||
2 |
|
R |
3 |
|
|
2 |
|
R |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
mu |
2 |
|
|
æ |
|
|
|
GM |
ö |
|
|
||||
mu0 |
|
|
|
|
ç GM |
|
÷ |
|
|
||||||||
|
- |
|
|
|
= mç |
|
- |
|
|
÷ |
, |
(1) |
|||||
2 |
|
2 |
|
R |
|
R |
|||||||||||
|
|
|
|
|
|
|
|
è |
3 |
|
|
|
|
ø |
|
|
|
где m – масса ракеты; M – масса Земли; G – гравитационная постоянная; u0 и υ – скорости ракеты относительно Земли в начальный и рассматриваемый моменты; Rз и R – расстояния от центра Земли до ракеты в начальный и рассматриваемый моменты.
После преобразования равенства (1) имеем:
u02 - u2 = 2GM (1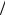 Rз -1
Rз -1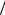 R).
R).
Ракета не вернется на Землю, если ее скорость υ в бесконечности будет равна нулю, т. е. υ = 0 при R → ∞ . В этом случае:
u02 = 2GM Rз . |
(2) |
Из закона всемирного тяготения [3.1] следует, что на поверх-
ности Земли GmM R2 |
= mg , откуда: |
3 |
|
GM = gRз2 , |
(3) |
где g – ускорение свободного падения на поверхности Земли.
Подставляя (2) в (3), находим u02 = 2gRз , или u0 = 
 2gRз .
2gRз .
Считая, что ракета приобретает нужную скорость u0 уже вблизи поверхности Земли, находим:
u0 = 
 2 × 9,8 × 6,37 ×106 =11,2 ×103 м/с = 11,2 км/с.
2 × 9,8 × 6,37 ×106 =11,2 ×103 м/с = 11,2 км/с.
54
Такая скорость необходима для преодоления гравитационного поля Земли. Она называется второй космической или параболической скоростью.
Ответ: υ0 = 11,2 км/с.
Пример 15. Через блок в виде диска, имеющий массу m = 80 г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m1 = 100 г и m2 = 200 г. С каким ускорением
будут двигаться грузы, если их представить самим себе? Трением пренебречь.
Дано:
m = 80 г = 0,080 кг, m1 = 100 г = 0,10 кг, m2 = 200 г = 0,20 кг.
Найти: a .
Решение. Применим к решению задачи основные законы поступательного и вращательного движения. На каждый из движущихся грузов действуют две силы: сила тяжести mg , направлен-
ная вниз, и сила T натяжения нити, направленная вверх. Используя решение примера 7 и рис. 1.13, можем записать:
T1 = m1 g + m1a , |
(1) |
T2 = m2 g − m2 a . |
(2) |
Согласно основному закону динамики вращательного движения относительно неподвижной оси [5.19], вращающий момент M , приложенный к диску, равен произведению момента инерции
I на его угловое ускорение ε : |
|
M = Iε . |
(3) |
Определим вращающий момент. Силы натяжения нитей действуют не только на грузы, но и на диск. По третьему закону Нью-
тона, силы T1′ и T2′ , приложенные к ободу диска, равны соответственно силам T1 и T2 , но по направлению им противоположны.
55

При движении грузов диск ускоренно вращается против часовой стрелки, следовательно, T2′ > T1′ . Вращающий момент, приложен-
|
|
|
|
|
|
|
|
|
ный к диску, равен разности моментов сил, |
||||||||||||
|
|
|
|
|
|
|
|
|
действующих на него, с учетом того, что |
||||||||||||
|
|
|
|
|
|
|
|
|
момент силы равен произведению силы на |
||||||||||||
|
|
|
|
|
|
|
|
|
плечо (радиус диска), т. е.: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
M = T |
′ |
r - T |
′ |
r = |
æ |
′ |
- T |
′ |
ö |
||
|
|
|
|
|
|
|
|
|
|
|
|
çT |
|
|
÷r , |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
è 2 |
|
1 |
|
ø |
|
|
|
|
|
|
|
|
|
где r – |
радиус |
диска. Вектор результи- |
||||||||||
|
|
|
|
|
|
|
|
|
рующего момента сил направлен вдоль |
||||||||||||
|
|
|
|
|
|
|
|
|
оси вращения OZ (рис. 1.17). Момент сил |
||||||||||||
|
Рис. 1.17 |
|
|
|
тяжести диска и реакции со стороны оси |
||||||||||||||||
|
|
|
|
|
|
|
|
|
вращения равен нулю, т.к. линии действия |
||||||||||||
этих сил |
|
пересекают |
|
|
ось вращения. |
Момент |
инерции диска |
||||||||||||||
I = mr 2 |
|
2 , |
угловое ускорение |
связано с |
линейным ускорением |
||||||||||||||||
грузов соотношением |
e = a r . Подставив в соотношение (3) вы- |
||||||||||||||||||||
ражения для M , I |
и ε , получим: |
|
|
|
|
|
|
|
|||||||||||||
æ |
|
¢ |
|
|
¢ ö |
mr 2 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
çT |
|
|
- T |
÷r = |
|
|
× |
|
|
, |
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
r |
|
|
|
|
|
|
|
|
|
|||||||
è |
2 |
|
|
1 |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откуда: T ¢ - T ¢ = |
ma |
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Так как T1′ = T1 и T2′ = T2′ , то можно заменить силы T1′ и T2′ их выражениями (1) и (2), тогда:
m2 g - m2 a - m1 g - m1a = m2 a , или
|
|
|
æ |
|
|
m ö |
|
(m |
|
- m )g = çm |
|
+ m + |
|
÷a , |
|
|
|
2 |
|||||
|
2 |
1 |
è |
2 |
1 |
ø |
|
откуда получаем окончательное выражение для ускорения:
|
m2 - m1 |
|||
a = |
|
|
|
g . |
m + m |
2 |
+ m 2 |
||
1 |
|
|
||
После подстановки числовых значений получим:
56
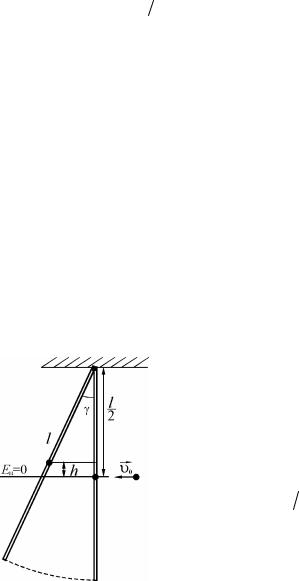
a = |
|
0,20 - 0,10 |
×10 = 2,88 м/с2. |
|
0,10 |
+ 0,20 + 0,08 2 |
|||
|
|
Ответ: a = 2,88 м/с2.
Пример 16. Стержень длиной l = 1,50 м и массой M =10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня (рис. 1.18). В середину стержня ударяет пуля массой m =10 г, летящая в горизонтальном направлении со скоростью u0 = 500 м/с, и застревает в стержне. На какой угол γ
отклонился стержень после удара?
Дано:
l= 1,50 м, M =10 кг,
m=10 г,
u0 = 500 м/с.
Найти: γ .
Решение. Удар пули следует рассматривать как неупругий: после удара и пуля, и соответствующая точка стержня будут двигаться с одинаковыми скоростями.
Рассмотрим подробнее явления, происходящие при ударе. Сначала пуля, ударившись о стержень, за ничтожно малый промежуток времени приводит его и саму себя в движение с угловой скоростью ω . Система приобретает кинетическую энергию вращательного движения [5.22]:
Eк = (I + I0 )w2 |
2 , |
(1) |
где I и I0 – |
моменты |
инерции |
стержня и пули относительно оси вращения соответственно.
Рис. 1.18
57
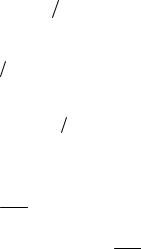
|
Учтем, что масса пули значительно меньше массы стержня |
||
( m << M ), следовательно, |
I0 << I . Пренебрегая I0 , (1) можно за- |
||
писать в виде: |
|
(1′ ) |
|
Eк = Iω2 2 . |
|
||
Затем стержень вместе с пулей поворачивается на искомый |
|||
угол |
γ , причем |
центр |
масс его поднимается на высоту |
h = (l |
2)(1 − cos γ), |
которая определяется, как в примере 9. В от- |
|
клоненном положении стержень (его центр масс) будет обладать потенциальной энергией [4.10]:
Eп = Mg(l 2)(1 − cos γ). |
(2) |
Потенциальная энергия получена за счет кинетической энергии и равна ей по закону сохранения механической энергии [4.12]. Приравняв правые части равенств (1) и (2), получим:
Mgl2 (1 − cos γ)= Iω2 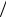 2 .
2 .
Отсюда cos γ =1 − Iω2 .
Mgl
Подставив в это соотношение выражение для момента инерции стержня [5.17] относительно оси, проходящей через один из
его концов, I = Ml 2 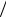 3 , получим:
3 , получим:
cos γ =1 − |
lω2 |
. |
(3) |
|
3g |
||||
|
|
|
Чтобы из выражения (3) найти γ , необходимо вначале опре-
делить значение угловой скорости ω . В момент удара на пулю и на стержень действуют силы (тяжести, реакции опоры), линии действия которых проходят через ось вращения. Моменты этих сил относительно оси вращения равны нулю. Поэтому при ударе пули о стержень будет справедлив закон сохранения момента импульса.
В начальный момент удара угловая скорость стержня ω0 = 0 , поэтому его момент импульса [5.12] L01 = Iω0 = 0. Пуля коснулась стержня и начала углубляться в стержень, сообщая ему угло-
58

вое ускорение и участвуя во вращении стержня около оси. Начальный момент импульса пули [5.11] L01 = mu0 r , где r – рас-
стояние точки попадания от оси вращения. В конечный момент удара стержень имел угловую скорость ω , а пуля – линейную скорость υ , равную линейной скорости точек стержня, находящихся на расстоянии r от оси вращения. Так как υ = ωr , то конечный
момент импульса пули L2 = mur = mr 2 w .
Применив закон сохранения момента импульса [5.21], можем записать:
L |
01 |
+ L |
02 |
= L + L |
2 |
, или mu |
0 |
r = Iw + mr 2 w, |
|||||||||||
откуда: |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
mu0 r |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
w = |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|||||
|
I + mr 2 |
|
|
|
|
|
|
|
|
|
|
||||||||
где I = Ml 2 |
3 – момент инерции стержня. |
||||||||||||||||||
Если учесть, что в (4) mr 2 |
<< I = Ml 2 3 , а также что |
||||||||||||||||||
то после несложных преобразований получим: |
|||||||||||||||||||
w = |
|
3mu0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2Ml |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставив числовые значения величин в (5), найдём: |
|||||||||||||||||||
w = |
|
3 ×10−2 |
× 500 |
= 0,50 с |
-1 |
|
|
|
|
|
|
||||||||
|
|
|
. |
|
|
|
|
|
|
||||||||||
|
|
2 ×10 ×1,5 |
1,5(0,50)2 |
|
|||||||||||||||
Из (3) получим: cos g =1 - |
» 0,99 , |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||
3 × 9,81
следовательно, g = 8°07′ .
Ответ: g = 8°07′ .
(4)
r = l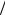 2 ,
2 ,
(5)
Пример 17. Маховик массой 4,0 кг свободно вращается с частотой 720 мин-1 вокруг горизонтальной оси, проходящей через его центр. Массу маховика считать равномерно распределенной по его ободу радиусом 40 см. Через 30 с под действием тормозящего момента маховик остановился. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.
59

Дано:
m= 4,0 кг,
n= 720 мин-1 =12 с-1,
t = 30 с,
R = 40 см = 0,40 м.
Найти: M , N .
Решение. Для определения тормозящего момента M сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения [5.20]:
M = I |
dw |
. |
|
|
|
|
|||
|
dt |
|
|
|
После интегрирования получим: |
||||
t |
|
ω |
|
|
M ò dt = I ò dw , Þ M (t - t0 )= I (w - w0 ), |
||||
0 |
|
ω0 |
|
|
M t = I |
ω , |
(1) |
||
где I – момент инерции маховика относительно оси, проходящей |
||||
через центр масс, |
ω – изменение угловой скорости за время t . |
|||
По условию задачи, Dw = - w0 = w0 , где w0 – начальная уг-
ловая скорость, так как конечная угловая скорость ω = 0 . Выразим начальную угловую скорость через частоту вращения маховика, тогда w0 = 2pn и ω = 2πn . Момент инерции маховика с учетом
того, что вся масса распределена по его ободу I = mR 2 , где m – масса маховика, R – его радиус. Тогда выражение (1) примет вид:
2pnmR2 = MDt ,
откуда M = 2pnmR2  Dt ,
Dt ,
числовое значение момента тормозящих сил:
M = 2 × 3,14 ×12 × 4,0 × 0,16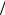 30 =1,61Н×м.
30 =1,61Н×м.
Так как тормозящий момент имеет постоянное значение, то угол поворота маховика до остановки может быть определен из выражения для равнозамедленного вращения [1.31]:
j = w0 Dt - eDt 2 2 , |
(2) |
где e – угловое ускорение.
60
