
get_2 физика
.pdfdLO |
r |
|
|
= M O . |
(5.3) |
||
dt |
|||
|
|
Закон сохранения момента импульса: если момент внешних сил относительно неподвижной точки О равен нулю, то момент импульса системы относительно этой же точки остается по- стоянным во времени, т.е.:
L = const . |
(5.4) |
Плечо силы относительно оси вращения – кратчайшее рас-
стояние от оси вращения до линии действия силы (перпендикуляр, проведенный от оси к линии действия силы).
Момент силы относительно оси вращения представляет собой проекцию вектора момента силы относительно точки O на направление оси вращения при условии, что точка O лежит на этой оси. Момент силы в этом случае равен произведению величины действующей силы на плечо:
M = Fl = Fr sin α , |
(5.5) |
где l – плечо силы (рис. 1.6), r – расстояние от оси вращения до точки приложения силы, α – угол между r и F .
Если сила вращает тело по часовой стрелке, то ее момент принято считать отрицательным, если же она вращает тело против часовой стрелки – положительным. Если же линия действия силы пересекает ось вращения или ей параллельна, то момент такой си-
лы будет равным нулю.
Уравнение моментов относительно оси вращения: произ-
водная по времени от проекции момента импульса материальной точки на ось вращения Z равна проекции момента действующей силы на эту же ось:
dLz |
= M z . |
(5.6) |
|
dt |
|||
|
|
||
|
|
21 |
Момент инерции материальной точки относительно некото-
рой оси – скалярная физическая величина, равная произведению ее массы на квадрат расстояния до оси вращения:
I = mr 2 |
, |
(5.7) |
где r – |
расстояние от оси вращения до материальной точки. |
|
Момент инерции системы материальных точек относи-
тельно оси – скалярная физическая величина, равная сумме произведений масс n материальных точек системы (частей тела) на квадраты их расстояний до оси вращения:
n |
|
|
I = å mi ri |
2 , |
(5.8) |
i=1 |
|
|
где mi – масса точки (части тела), ri |
– расстояние от оси враще- |
|
ния до точки (части тела). |
|
|
Момент инерции сплошного твердого тела: |
||
I = ò r 2 dm , |
I = ρò r 2 dV , |
(5.9) |
|
V |
|
где ρ – плотность тела, V – объем тела.
Момент импульса материальной точки относительно оси представляет собой проекцию вектора момента импульса материальной точки на ось вращения и равен произведению величины импульса точки на плечо:
L = pl = pr sin α , |
(5.10) |
где l – плечо (рис. 1.7), |
r – расстояние от оси вращения до точки, |
α – угол между r и p . |
|
Если материальная точка вращается по окружности радиуса r , то
момент импульса относительно оси вращения равен: |
|
L = mυr . |
(5.11) |
Для системы материальных точек (твердого тела) момент импульса относительно оси есть сумма моментов импульсов движения отдельных точек (частей тела):
22

L = |
å |
m |
υ r = ω |
m r 2 |
= Iω. |
(5.12) |
|
|
i |
i i |
å |
i i |
|
|
|
|
i |
|
|
i |
|
|
|
Момент инерции тонкого полого цилиндра радиуса R относительно его геометрической оси:
I = mR 2 . |
(5.13) |
Момент инерции тонкого сплошного цилиндра |
|
или диска радиуса R относительно его |
|
геометрической оси: |
|
I = mR2 2 . |
(5.14) |
Момент инерции шара радиуса R относительно его геометрической оси:
I = (2 5)mR2 . |
(5.15) |
Момент инерции тонкого стержня длины l |
|
относительно оси, перпендикулярной стержню |
|
и проходящей через его центр масс: |
|
I = ml 2 12 . |
(5.16) |
Момент инерции тонкого стержня длиной
l относительно оси, перпендикулярной стержню и
проходящей через один из его концов:
I = ml 2 3 . |
(5.17) |
Теорема Гюйгенса-Штейнера для нахождения момента инерции твердого тела относительно произвольной оси: момент инерции тела относительно некоторой произвольной оси Z равен моменту инерции относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела на квадрат расстояния между осями:
I z = Icz + md 2 , |
(5.18) |
|
23 |
где Icz – момент инерции относительно оси, проходящей через центр масс, d – расстояние между этими осями.
Вращение абсолютно твердого тела вокруг неподвижной оси под действием момента сил описывается основным уравнением
динамики вращательного движения:
r |
(5.19) |
Iε = M . |
Используя выражение для момента импульса твердого тела при вращении относительно оси, можно получить соотношения, устанавливающие связь между моментом силы, моментом инерции,
угловой скоростью и угловым ускорением: |
|
||||||||
r |
|
r |
|
r |
r |
|
|||
|
d(Iω) |
|
|
dω |
|
||||
M = |
dL |
= |
|
= I |
= Iε . |
(5.20) |
|||
dt |
dt |
dt |
|||||||
|
|
|
|
|
|||||
Закон сохранения момента импульса: момент импульса системы материальных точек (твердого тела) относительно неподвижной оси вращения сохраняется, т. е. не изменяется с течением времени, в случае равенства нулю момента внешних сил:
n r
å Ii ωi = const .
i=1
Кинетическая энергия тела, вращающегося относительно неподвижной оси:
Eвр = Iω2 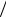 2 .
2 .
Кинетическая энергия тела, катящегося по плоскости без проскальзывания ( υ = ωr ):
Eк = mυ2 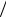 2 + Iω2
2 + Iω2 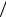 2 ,
2 ,
(5.21)
(5.22)
(5.23)
где первое слагаемое – кинетическая энергия поступательного движения центра масс, а второе – кинетическая энергия вращения тела относительно оси, проходящей через центр масс.
24
Работа при вращательном движении твердого тела:
δA = Mdϕ , |
(5.24) |
A = ò Mdϕ , |
(5.25) |
где M – момент внешних сил относительно оси вращения, dϕ – изменение угла поворота под действием момента сил.
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Колебания – это движения или процессы, характеризующиеся определенной повторяемостью во времени. Механические колебания характеризуются периодическими изменениями величин, описывающих механическое движение.
Колебания, при которых смещение изменяется по закону синуса или косинуса, называются гармоническими.
Колебания системы, совершаемые за счет первоначально сообщенной ей энергии без внешних воздействий, называются свободными. При отсутствии сил трения свободные колебания будут незатухающими (протекающими бесконечно долго).
Дифференциальное уравнение свободных гармонических колебаний:
&& |
|
|
2 |
|
|
|
|
(6.1) |
x |
+ ω0 x = 0 , |
|
||||||
где |
&& |
= |
d 2 x |
, ω0 |
= 2π T = 2πν – циклическая частота собственных |
|||
|
|
|
||||||
x |
dt |
2 |
|
|||||
|
|
|
|
|
|
|
||
колебаний.
Решением этого дифференциального уравнения является уравне-
ние гармонических колебаний:
x = xmax cos(ω0t + ϕ0 ), |
(6.2) |
где ϕ0 – начальная фаза, ϕ = ω0t + ϕ0 – фаза, xmax – амплитуда колебаний.
Фаза – физическая величина, характеризующая положение колеблющейся системы в любой момент времени.
25
Амплитуда колебаний – максимальное значение периодически изменяющейся, т.е. колеблющейся, величины.
Полная механическая энергия тела при гармоническом коле-
бательном движении постоянна и равна сумме его кинетической и потенциальной энергий:
E = Eк + Eп = |
mω2 x2 |
= const . |
|
|
max |
(6.3) |
|||
2 |
||||
|
|
|
Период колебаний – промежуток времени, за который совершается одно полное колебание.
Период колебаний математического маятника:
T = 2π |
|
l |
, |
(6.4) |
||
g |
||||||
|
|
|
|
|
||
где l – длина маятника, |
g – ускорение свободного падения. |
|||||
Период колебаний пружинного маятника: |
||||||
T = 2π |
|
m |
|
, |
(6.5) |
|
|
|
k |
|
|
|
|
где m – масса маятника, k – коэффициент пропорциональности между силой и смещением в законе Гука (коэффициент жесткости пружины).
Период колебаний физического маятника:
T = 2π |
|
I |
|
, |
(6.6) |
|
mga |
||||
где I |
– момент инерции относительно оси вращения, |
a – рас- |
|||
стояние от оси вращения до центра тяжести.
7.ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Релятивистская механика изучает движение тел, имеющих скорость, близкую к скорости света в вакууме.
26
Энергия покоя частицы: |
|
E0 = m0c2 , |
(7.1) |
где m0 – масса покоя частицы, c – скорость света в вакууме.
Релятивистская масса:
m = |
m0 |
, |
(7.2) |
1 - u2
c2
где υ – скорость движения частицы относительно инерциальной системы отсчета.
Релятивистский импульс:
p = mu , |
p = |
|
m0 u |
|
. |
(7.3) |
|
|
|
|
|
||||
|
|
1 - |
u2 |
|
|||
|
|
c |
2 |
|
|
||
|
|
|
|
|
|
||
Полная энергия частицы:
E = mc2 = |
m |
c2 |
|
|
||
0 |
|
|
|
. |
||
|
|
|
|
|
||
|
1 - |
u2 |
||||
|
c |
2 |
|
|||
|
|
|
|
|
||
Кинетическая энергия релятивистской частицы:
|
|
æ |
1 |
ö |
||
Eк = E - E0 = m0 c |
2 |
ç |
÷ |
|||
|
ç |
|
|
|
-1÷ . |
|
|
|
|
|
|||
|
1 - u2 c2 |
|||||
|
|
è |
ø |
|||
Лоренцево сокращение длины в релятивистской механике:
(7.4)
(7.5)
l = l0 |
1 - |
u2 |
, |
(7.6) |
|
c2 |
|||||
|
|
|
|
||
где l0 |
– |
длина покоящегося стержня (собственная длина), l – |
|||
длина стержня, движущегося со скоростью υ (близкой к скорости света) относительно лабораторной (условно неподвижной) инерциальной системы. Стержень расположен вдоль оси, совпадающей с направлением движения.
27
Замедление хода движущихся часов в релятивистской механике:
t = |
t0 |
, |
(7.7) |
1 − υ2
c2
где t0 – собственное время движущихся часов (интервал време-
ни между двумя событиями, которые произошли в одной и той же точке собственной системы отсчета, связанной с движущимся со скоростью υ объектом), t – интервал времени относительно лабораторной (неподвижной) системы отсчета, измеренный по часам, находящимся в разных точках пространства этой системы.
Релятивистское уравнение динамики частицы:
|
dp |
|
r |
|
|
= F , |
(7.8) |
||
|
dt |
|||
|
p = mυ – релятивистский импульс частицы. |
|
||
где |
|
|||
8. ЭЛЕМЕНТЫ МЕХАНИКИ СПЛОШНЫХ СРЕД
Давление жидкости – физическая величина, определяемая отношением силы Fн , действующей со стороны жидкости на пло-
щадку S перпендикулярно ее поверхности к величине ее площади:
p = |
Fн |
. |
(8.1) |
|
|||
|
S |
|
|
Единицей измерения давления в системе СИ является один Паскаль (1 Па). 1 Па равен давлению, оказываемому силой в 1 Н, действующей нормально на площадку 1 м2.
Закон Паскаля: давление, оказываемое на жидкость (газ), пере-
дается по всем направлениям и во все точки в объеме жидкости (газа) одинаково.
Если жидкость слабо сжимаема, то ее плотность практически не зависит от давления.
28

Гидростатическое давление столба несжимаемой жидкости изменяется линейно с высотой, т.е.
p = ρgh , |
(8.2) |
где ρ – плотность жидкости, g |
– ускорение свободного падения, |
h – высота столба жидкости.
Закон Архимеда: на тело, погруженное в жидкость (газ), дей- ствует со стороны этой жидкости (газа) направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа):
FA = ρgV , |
(8.3) |
где ρ – плотность жидкости или газа, куда помещено тело, V – объем погруженной в жидкость или газ части тела.
Движение жидкости (газа) называется течением. Линия, в каждой точке которой касательная к ней совпадает с направлением вектора скорости частиц жидкости (газа), называется линией тока.
Трубка тока – часть жидкости (газа), ограниченная линиями тока.
Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока, что отражается в уравнении неразрывности
струи:
S1υ1 = S2 υ2 , |
(8.4) |
где υ1 и υ2 – скорости движения потока в поперечных сечениях S1 и S2 трубки тока соответственно.
При стационарном* течении идеальной, т.е. невязкой, жидкости (газа) выполняется закон сохранения энергии, который представ-
ляет собой уравнение Бернулли: сумма динамического, гидро- статического и статического давлений при стационарном тече-
* При стационарном течении скорости потока в каждом сечении не изменяются со временем.
29
нии среды есть величина постоянная для всех точек данной линии тока, т.е.:
p + |
ρυ2 |
+ ρgh = const , |
(8.5) |
|
2 |
||||
|
|
p – статическое давление, |
||
где ρ – плотность жидкости или газа, |
||||
h – высота, на которой находится сечение трубки тока по отношению к нулевому уровню (для горизонтальных трубок h = 0 ),
ρgh – гидростатическое давление, |
ρυ2 |
– динамическое давление |
|
2 |
|||
|
|
(обусловленное движением жидкости).
Нормальное напряжение при растяжении-сжатии:
σ = |
|
F |
, |
|
|
|
(8.6) |
|
|
|
|
|
|||
|
|
S |
|
|
|
|
|
где F – нормальная составляющая силы (перпендикулярно попе- |
|||||||
речному сечению), приложенной к стержню, S |
– площадь попе- |
||||||
речного сечения стержня. |
|
||||||
Относительная деформация: |
|
||||||
ε = |
l − l0 |
= |
l |
, |
(8.7) |
||
|
l0 |
l0 |
|||||
|
|
|
|
|
|||
где l0 и l – первоначальная и конечная длина стержня соответственно, l – абсолютная деформация.
Пластическая деформация – деформация, которая сохраняется в теле после прекращения действия внешних сил.
Упругая деформация наблюдается в случае, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму тела.
Закон Гука для растяжения-сжатия (упругие деформа-
ции): для малых деформаций относительное удлинение и напря- жение пропорциональны друг другу:
σ = εE , |
(8.8) |
30
