
stat_2
.pdfЦель работы
Часто на практике необходимо исследовать, как изменение одной переменной величины X влияет на другую величину Y. Например, как количество цемента X влияет на прочность бетона Y. Такое влияние иногда может описываться простой функциональной связью Y = F (X) между переменными. Однако для многих изучаемых процессов это скорее исключение, чем правило. Тем не менее, исследователь все-таки отмечает некую существенную связь между переменными. Эта, так называемая, корреляционная связь и будет предметом нашего изучения в данной лабораторной работе. На основе статистического анализа полученных экспериментальных данных, которые будут представлены, как
правило, в виде таблицы чисел (x1, y1), (x2, y2), ..., (xn, yn), студент долженнаучитьсяследующему:
-устанавливать наличие или отсутствие связи (корреляционной) между изучаемыми величинами X и Y;
-предсказывать тип зависимости между переменными X и Y, то есть выдвигать модель исследуемой связи (как правило, это будет полином не слишком высокой степени);
-оценивать параметры предложенной модели, например, коэффициенты соответствующего полинома;
-проверять адекватность построенной модели реальному процессу, то есть овладеть процедурой проверки гипотез о значимости упомянутых коэффициентов.
Содержание работы
1. Установление наличия корреляционной зависимости между случайными величинами X и Y:
-определение выборочного коэффициента корреляции по результатам выборки (эксперимента);
-установление значимости выборочного коэффициента корреляции;
-выводы о зависимости или независимости случайных величин
X и Y.
3
2.Выбор регрессионной модели и ее статистический анализ:
-выбор уравнения регрессии;
-оценка коэффициентов регрессионного уравнения по методу наименьших квадратов;
-проверка точности оценки регрессии и установление адекватности выбранной модели изучаемому процессу.
Порядок проведения работы
-Изучить теоретический материал.
-По данным выборки найти выборочный коэффициент корреляции rXY .
-Установить значимость отличия от нуля rXY .
-Если сделан вывод о том, что между X и Y существует корреляционная связь, выбрать уравнение линии (модель) регрессии
Y на X.
-Оценить параметры выбранной модели по результатам выборки.
-Проверить точность оценки регрессии, то есть найти доверительные интервалы для параметров регрессии.
-Провести расчеты на ПЭВМ.
-Сделать основные выводы.
-Составить отчет о выполнении работы.
Требования к отчету
Отчетовыполненииработыдолженсостоятьизследующихразделов:
Постановка задачи. Анализ решения задачи. Результаты счета на ПЭВМ.
Основные выводы и рекомендации.
4
1. УСТАНОВЛЕНИЕ НАЛИЧИЯ ЗАВИСИМОСТИ МЕЖДУ ДВУМЯ СЛУЧАЙНЫМИ ВЕЛИЧИНАМИ ПО РЕЗУЛЬТАТАМ ИХ ВЫБОРОК
В предыдущей лабораторной работе мы изучали одну случайную величину X, ее вероятностные и статистические характеристики, полученные на основе имеющейся выборки значений этой случайной величины. Большой интерес для широкого класса научных и инженерных задач представляет обнаружение взаимных связей между двумя и более случайными величинами. Например, существует ли связь между курением и ожидаемой продолжительностью жизни, или между умственными способностями и успеваемостью. Очевидно, что привычной для нас строгой функциональной зависимости, когда каждому значению X по определенному правилу соответствует значение Y, то есть Y = f (X), здесь мы установить не можем. Слишком много самых различных случайных факторов влияют как на величину X, так и на величину Y. Тем не менее, зачастую невооруженным глазом видно, что какая-то зависимость между изучаемыми величинами X и Y существует. Например, вес и рост человека, естественно, тесно связаны между собой, но они не определяют друг друга однозначно. Точно так же прочность бетона, очевидно, зависит от количества цемента, но эта зависимость явно не функциональная.
Рассмотрим задачу о том, как сделать надежный вывод о наличии или отсутствии зависимости между двумя случайными величинами на основе экспериментальных данных. Слово «надежный» означает (как и в лабораторной работе №1), что вероятность истинности сделанного вывода должна быть близка к единице.
Для исследования такой зависимости во второй половине XIX века английский ученый Фрэнсис Гальтон (двоюродный брат Чарльза Дарвина) и его ученики (например, Карл Пирсон) ввели такие важные понятия, как корреляция и регрессия, которые стали основными понятиями в теории вероятностей и математической статистике, а также в связанных с ними научных дисциплинах. При этом саму зависимость между случайными величинами назвали
корреляционной.
5

1.1.Коэффициент корреляции
Винженерных приложениях упомянутая выше задача о наличии зависимости между двумя случайными величинами обычно сводится к установлению связи между некоторыми предполагаемыми
возбуждениями-факторами x1, x2, .., xn и наблюдаемым откликом y изучаемой системы (рис. 1.1).
x1
x2
y
xn
Рис. 1.1
Рассмотрим вначале взаимосвязь между одним фактором x и откликом y, то есть взаимосвязь между двумя случайными величинами X и Y. В теории вероятностей для установления степени зависимости между двумя случайными величинами вводится числовая характеристика, которая называется коэффициентом корреляции или просто корреляцией. При этом такую зависимость называют
корреляционной зависимостью. Для двух случайных величин X и Y
коэффициент корреляции определяется следующим образом:
ρX Y = ρ(X ,Y ) = |
M[(X − M X )(Y − MY )] |
, |
(1.1) |
|
σX σY |
||||
|
|
|
где M X , σX и MY , σY – математическое ожидание и среднеквадратическое отклонение случайных величин X и Y соответственно.
Величину, которая стоит в числителе правой части этой формулы, называют ковариацией и часто обозначают C( X ,Y ) :
C ( X ,Y ) =M[(X − M X )(Y − MY )] .
Легко увидеть, что если X = Y, то
C(X , X ) =σ2X , C(Y ,Y ) =σY2 .
6
При этом выполняется неравенство
| C(X ,Y ) | ≤ σX σY .
Это означает, что коэффициент корреляции заключен между −1 и 1:
−1 ≤ ρ( X ,Y ) ≤ 1 .
Формулу для коэффициента корреляции (1.1) легко преобразовать в более наглядную и удобную с точки зрения вычислений. Учитывая, что
M[(X − M X )(Y − MY )] = M[XY − XM X −YMY + M X MY ] = = M ( XY ) − M X MY − MY M X + M X MY = M ( XY ) − M X MY ,
получаем формулу:
ρ(X ,Y ) = M (XY ) − M X MY .
σX σY
Если случайные величины X и Y – независимы, то коэффициент корреляции ρ( X ,Y ) =0 , так как M (X Y ) =M (X ) M (Y ) . Обратное утверждение, вообще говоря, неверно, то есть, некоррелированные случайные величины не обязательно независимы.
Определенный выше коэффициент корреляции принадлежит к числу наиболее трудных для понимания числовых характеристик случайных величин. Если такие характеристики, как частота, вероятность, математическое ожидание, дисперсия, стандартное отклонение, осознаются достаточно легко, то термин "коэффициент корреляции" оказывается сложным для понимания. Это объясняется в первую очередь сложностью математического выражения для этого коэффициента и отсутствием соответствующего понятия в повседневной жизни. Поэтому напомним здесь основные свойства коэффициента корреляции:
1.Коэффициент корреляции ρ(X ,Y ) симметричен относительно X и Y и может изменяться в пределах от −1 до 1.
7

2.Равенство | ρ( X ,Y ) | =1 указывает на наличие точной ли-
нейной связи вида y = ρσσYX (x − M X ) +MY между рассматриваемыми величинами X и Y, возможные значения которых в этом случае расположены на одной прямой.
3.При значениях ρ(X ,Y ) , по модулю близких к единице, точки с координатами X и Y с большой вероятностью располагаются в окрестностях некоторой прямой, непараллельной ни одной из осей координат. По мере уменьшения | ρ(X ,Y ) | эта вероятность падает, и при ρ(X ,Y ) , близком к нулю, такая прямая вообще не может быть обнаружена. Однако это не исключает возможности нелинейной связи между рассматриваемыми величинами.
Таким образом, коэффициент корреляции является характеристикой степени зависимости между двумя случайными величинами. В заключение отметим, что
-при | ρ( X ,Y ) | =1 величины X и Y являются полностью коррелированными; при | ρ(X ,Y ) | , близком к единице; – сильно коррелированными; при ρ(X ,Y ) , близком к нулю; – слабо коррелированными и при ρ(X ,Y ) = 0 – некоррелированными;
-при ρ(X ,Y ) > 0 корреляционная связь между величинами X
иY – положительная; при ρ(X ,Y ) < 0 – отрицательная. При этом в первом случае возрастанию X с большой вероятностью соответствует возрастание Y, а во втором – убывание.
1.2. Представление исходных данных
Приступая к анализу экспериментальных данных, мы не имеем сведений о наличии корреляционной связи между случайными величинами X и Y. Поэтому первая задача, которую необходимо решить,
– это сделать обоснованный вывод о наличии этой зависимости или об отсутствии таковой. Как и в случае исследования одной случайной величины, материалом, на базе которого мы решаем эту задачу, является выборка значений случайных величин X и Y.
8

Пусть в результате n экспериментов (проведенных в одних и тех жеусловиях) зафиксированыn парзначений(x1, y1), (x2, y2),..., (xn, yn), где xi – значение, которое приняла случайная величина X в i-м эксперименте, а yi – значение, которое приняла случайная величина Y в этом же эксперименте. Этот набор данных называется выборкой объема n пары случайных величин.
В случае большого объема выборки (n – достаточно велико) и частого повторения в выборке некоторых значений xi и yi ее удоб-
но представлять в виде корреляционной таблицы
X \ Y |
y1 |
y2 |
… |
yl |
|
x1 |
m11 |
m12 |
… |
m1l |
mX1 |
x2 |
m21 |
m22 |
… |
m2l |
mX 2 |
… |
… |
… |
|
… |
… |
xk |
mk1 |
mk 2 |
… |
mkl |
mX k |
mY |
mY |
… |
mY |
1 |
2 |
|
l |
Здесь mij – частота появления пары значений (xi , y j ) в выборке; x1 < x2 <... < xk – различные значения, которые приняла случайная величина X; mX1 ,..., mX k – частоты появления этих значений в вы-
k
борке (∑mX i = n) . Аналогично, y1 < y2 <... < yl – различные зна-
i=1
чения, которые приняла случайная величина Y; mY1 ,..., mYl – часто-
l
ты появления этих значений в выборке (∑mYi = n) .
i=1
Если при большом объеме выборки велико также и число различных значений xi и yi , то таблицу имеет смысл представить в виде интервальной корреляционной таблицы (аналог группированного статистического ряда, см. лабораторную работу №1)
9

X \ Y |
[ y |
, y ) |
[ y , y |
2 |
) |
… |
[ y − |
, y ] |
|
0 |
1 |
1 |
|
|
l 1 |
l |
|
[x0 , x1) |
m11 |
m12 |
|
|
… |
m1l |
||
[x1, x2 ) |
m21 |
m22 |
|
… |
m2l |
|||
… |
… |
… |
|
|
|
… |
||
[xk −1, xk ] |
mk1 |
mk 2 |
|
… |
mkl |
|||
Здесь частота mij – количество пар значений (xζ, yθ) выборки, для которых значение xζ попадает в интервал [xi−1, xi ) , а значение yθ – в интервал [ y j −1, y j ) . Количество интервалов, их длина, а также граничные значения x0 , y0 , xk , yl определяются так же, как и для группированного статистическогоряда(см. лабораторнуюработу№1, с. 22–23).
Замечание. Следует отметить, что часто информация для статистического исследования сразу поступает в виде интервальной корреляционной таблицы.
Для дальнейших вычислений информацию, представленную в виде интервальной корреляционной таблицы, надо преобразовать в обычную корреляционную таблицу, взяв в качестве значений вариант середины соответствующих интервалов,
|
X \ Y |
|
y* |
|
|
|
y* |
… |
y* |
|
|
|
|
|
1 |
|
|
|
2 |
|
l |
|
|
x* |
|
m11 |
|
|
m12 |
… |
m1l |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x* |
|
m21 |
|
|
m22 |
… |
m2l |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
… |
|
… |
|
|
… |
|
… |
|
|
|
xk* |
|
mk1 |
|
|
mk 2 |
… |
mkl |
|
Здесь x* = |
x + x |
, y* = |
y j + y j −1 |
|
|
|
||||
i i−1 |
|
|
|
. |
|
|
||||
|
|
|
|
|
|
|
||||
|
i |
2 |
|
j |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разберем сказанное на примере. Пусть получена выборка случайных величин X и Y (X – рост студента в см, Y – его масса в кг).
10

Таблица. Данныеоростеимассестудентов(X –роствсм, Y – массавкг):
|
X |
|
178 |
188 |
178 |
|
165 |
175 |
185 |
|
183 |
175 |
183 |
|
|
Y |
|
63 |
95 |
67 |
|
66 |
83 |
75 |
|
70 |
77 |
79 |
|
|
|
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
X |
|
193 |
188 |
183 |
|
173 |
178 |
|
173 |
185 |
|
|
|
|
Y |
|
70 |
84 |
84 |
|
75 |
100 |
84 |
|
82 |
77 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
165 |
185 |
188 |
|
163 |
183 |
183 |
|
170 |
185 |
|
|
|
Y |
|
61 |
79 |
82 |
|
68 |
77 |
75 |
|
66 |
77 |
|
|
Объем |
выборки n = 25. |
Найдем количество интервалов по формуле |
||||||||||||
k≥[log2 n]+1 (см. лабораторнуюработу№1, с.33), k≥[log2 25]+1=4+1=5 .
Итак, можно взять k = 5. Так как xmin =163 и xmax =193 , то длина интер-
вала для случайной величины X будет равна h = |
193−163 |
=6 , |
x |
|
=163 , |
|||
|
|
0 |
||||||
|
x |
5 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x5 |
=193 . Аналогично, ymin =61, ymax =100, hy = |
100−61 |
=7,8 . Округлим |
|||||
|
||||||||
|
|
|
5 |
|
|
|
|
|
hy до 8 и возьмем y0 =60 , y5 =100 . Построим интервальную корреляционнуютаблицу
X \ Y |
[60;68) |
[68;76) |
[76;84) |
[84;92) |
[92;100] |
[163;169) |
2 |
1 |
|
|
|
[169;175) |
|
1 |
1 |
|
|
[175;181) |
3 |
|
2 |
1 |
1 |
[181,187) |
|
3 |
5 |
1 |
|
[187,193] |
|
1 |
1 |
1 |
1 |
Преобразуем ее в обычную корреляционную таблицу |
|
||||||
|
|
|
|
|
|
|
|
|
X \ Y |
64 |
72 |
80 |
88 |
96 |
mY j |
|
166 |
2 |
1 |
|
|
|
3 |
|
172 |
3 |
1 |
1 |
|
|
2 |
|
178 |
|
2 |
1 |
1 |
7 |
|
|
184 |
|
3 |
5 |
1 |
|
9 |
|
190 |
|
1 |
1 |
1 |
1 |
4 |
|
mX i |
5 |
6 |
9 |
3 |
2 |
25 |
11
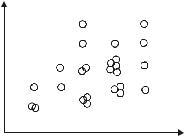
Пустые клетки означают, что соответствующая им частота равна 0. Для большей наглядности исходные данные представляют в ви-
де так называемого корреляционного поля (рис. 1.2).
Y
96
88
80
72
64
X
0 |
166 |
172 |
178 |
184 |
190 |
Рис. 1.2
Для этого в системе координат xOy строят точки (xi , y j ) , причем их
количество соответствует частоте из корреляционной таблицы. При частоте, большей единицы, изображается облако близко расположенных друг к другу точек с соответствующими координатами.
1.3.Оценка коэффициента корреляции по результатам эксперимента
Пусть имеется выборка значений пары случайных величин X и Y, которая представлена в виде набора (x1, y1), (x2, y2),..., (xn, yn) или в виде корреляционной таблицы.
По аналогии с оценками математического ожидания и дисперсии будем утверждать, что достаточно хорошей оценкой коэффициента корреляции ρ(X ,Y ) будет выборочный коэффициент корреляции
r ( X ,Y ) , определяемый формулой
|
|
n |
|
|
|
|
|
||||
|
∑(xi − |
X |
)( yi − |
Y |
) |
|
|||||
r (X ,Y ) = ρ( X ,Y ) = |
|
i=1 |
. |
||||||||
n |
|
|
|
n |
|
|
|
|
|||
[∑ |
(xi − |
X |
)2 ∑( yi − |
Y |
)2 ]1/ 2 |
|
|||||
|
i=1 |
|
|
|
i=1 |
|
|||||
12
