
stat_2
.pdf
4. МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
При решении инженерных задач часто требуется найти зависимость между случайной величиной η и переменными величинами
ξ1,ξ2 , ...,ξm , значения которых x1 , x2 ,..., xm задаются заранее при планировании эксперимента. Однако при проведении n экспериментов эти значения x1 j , x2 j , ..., xmj ( j =1, n) обычно измеряются с
некоторыми малыми ошибками (погрешности приборов и т.п.). Неизвестные значения ξ1,ξ2 , ...,ξm могут иметь случайную ва-
риацию, а значения x1 , x2 , ..., xm не являются случайными, так как они заданы заранее. При таком подходе величины xi (i =1, m) назы-
вают контролируемыми переменными.
Так как переменные xi не коррелированы с ошибками измерений, то для получения зависимости между xi и у, где у – значение случайной величины η, можно использовать обычный метод наименьших квадратов, как и ранее, при рассмотрении случая линейной регрессии двумерного случайного вектора.
Заметим, что переменная η является случайной величиной, так как
при проведении эксперимента невозможно учесть все факторы, оказывающиевлияниенаэтупеременную, втомчислеошибкиизмерений.
При исследовании взаимосвязи между случайной величиной η и переменными ξ1 , ξ2 , ..., ξm обычнорассматриваютсяследующиевопросы:
-выбор модели регрессии;
-нахождение оценок параметров выбранного уравнения и построение доверительных интервалов параметров уравнения по заданному уровню значимости α;
-проверка согласованности выбранной модели с эксперименталь-
ными данными и уточнение вида полученного уравнения. Выбор модели регрессии производится обычно из эмпирических
соображений. Эту задачу здесь мы рассматривать подробно не будем ввиду ее сложности.
Далее рассматриваются две задачи:
33

-построение линейного уравнения регрессии и доверительных интервалов для его параметров;
-проверка согласованности полученной модели с экспериментальными данными наиболее простыми способами.
4.1 Нахождение оценок параметров линейного уравнения регрессии
Ограничимся построением линейного уравнения регрессии
η = α*0 + α1*ξ1 + α*2ξ2 +... + α*mξm .
Другими словами будем искать наилучшее приближение функции η функцией вида
ϕ(x1 , ..., xm , a0 , a1 , ..., am ) = a0 + a1 x1 +... + am xm .
Пусть в j-м эксперименте величины ξ1 , ξ2 , ..., ξm приняли значения x1 j , x2 j , ..., xm j , а случайная величина η – значения y j ( j =1,n) .
Согласно методу наименьших квадратов в качестве оценок параметров α*0 , α1* , ..., α*m принимаются значения a0* , a1* , ..., am* , при которых достигает минимума функция
n
Φ(a0 , a1 , ..., am ) = ∑( y j −a0 −a1 x1 j −...am xm j )2 .
j =1
Из необходимых условий экстремума функции Φ(a0 , a1, ..., am ) следует, что параметры a0 , a1, ..., am являются решениями системы
∂Φ(a0 , a1 , ..., am ) = 0, i = 0, 1, ..., m
∂ai
Введем следующие обозначения:
X – n ×(m +1) -мерная матрица наблюдений контролируемых пе-
ременных, в которую введен дополнительно первый столбец, состоящий из единиц;
Y – n-мерный вектор-столбец наблюдаемых значений случайной величины η;
34

A – (m +1) -мерный столбец параметров ai (i = 0, 1, ..., m) :
1 |
x |
... |
x |
|
|
|
|
|
11 |
|
m1 |
|
|
|
1 |
x12 |
... |
xm2 |
|
Y |
X = |
|
|
... ... |
, |
||
... ... |
|
|
||||
|
1 |
x |
... |
x |
|
|
|
|
1n |
|
mn |
|
|
y1
=y2
...
yn
|
a |
|
|
0 |
|
|
a1 |
|
, |
A = |
. |
|
... |
|
|
|
|
|
am |
|
В матричных обозначениях эта система примет вид
|
(X T X )A = X TY , |
здесь X T – |
матрица, транспонированная к матрице X. Решение |
этой системы находим по формуле |
|
|
A = (X T X )−1 X TY , |
где ( X T X )−1 |
– матрица, обратная матрице ( X T X ) . Искомое выбо- |
рочное уравнение регрессии имеет вид:
y = a0 + a1x1 +... + am xm .
При большом числе переменных задача нахождения вектора решается на ЭВМ с помощью стандартных программ.
4.2 Построение доверительных интервалов параметров уравнения регрессии
Построение доверительных интервалов параметров ai (i=0, 1, ..., m) легко проводится в случае, если остатки εj = y j − y j ( j =1, n) распределены по нормальному закону с параметрами M (ε) = 0, D(ε) = σ2 .
Здесь y j – наблюдаемое в j-м эксперименте значение η, y j – зна-
чение y, полученное из уравнения регрессии при подстановке значений x1 j , x2 j , ..., xm j , заданных в j-м эксперименте. При малом
числе опытов (n < 50) применяют приближенные методы проверки нормального распределения остатков. Можно считать, что остатки
35
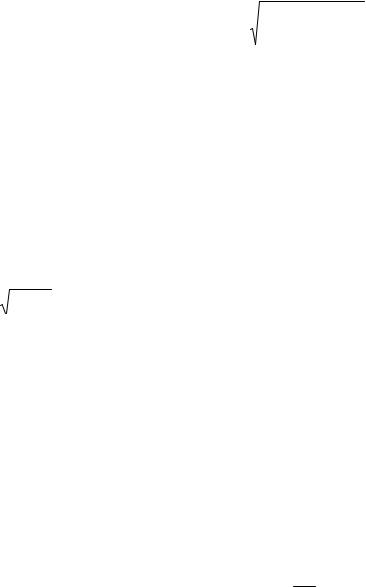
εj распределены по нормальному закону, если не менее 95% из
n
них лежат в интервале ( −2Sε, 2Sε) , где Sε = ∑ε2j /(n − m +1) –
j =1
оценка дисперсии.
Случай, когда остатки ε j не подчиняются нормальному закону
распределения, рассматривать не будем ввиду его сложности.
Для построения 100 (1 −α)% -х доверительных интервалов для α*j ( j = 0, 1, ..., m) по таблице распределения Стьюдента по заданному уровню значимости α и числу степеней свободы ν = n − m −1
находим критическое значение статистики t |
α (ν) . Доверительные |
|
1− |
2 |
|
интервалы имеют вид |
||
|
|
a −t |
α |
(ν) S |
ai |
< α* < a +t |
α |
(ν) S |
a i |
, |
|||
|
i |
1− |
|
i |
i |
1− |
|
|
||||
|
|
2 |
|
|
|
|
2 |
|
|
|
||
где Sa = Sε |
ai(+−1,1)i+1 , i = 0,1,...,m . |
|
|
|
|
|
|
|||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
Здесь Sa i |
– средние квадратические ошибки коэффициентов ai , |
|||||||||||
Sε – вычисленная выше оценка дисперсии, |
ai(+−1,1)i+1 – диагональный |
|||||||||||
элемент матрицы (X T X)−1 |
размера |
(m +1)×(m +1) , соответствую- |
||||||||||
щий переменной xi . |
|
|
|
|
|
|
|
|
|
|
||
4.3 Проверка согласованности модели с экспериментальными данными
Если в уравнении регрессии какая-то из контролируемых переменных xi незначимо влияет на переменную у, то эту переменную xi следует исключить из уравнения регрессии.
Выявление статистически незначимых переменных xi можно рассматривать как проверку гипотезы H0 : α*i = 0 (i =1,m) , то есть η не коррелирована с ξi .
36

Если остатки εj распределены по нормальному закону, то гипо-
теза H0 может быть проверена с помощью статистик ti = ai , i =1, m .
Sai
Эти статистики имеют распределение Стьюдента с ν = n −m −1 степенями свободы при условии справедливости гипотезы H0 .
По таблицам распределения Стьюдента находим критическое
значение t α (ν) , где α – выбранный уровень значимости. Если
1− 2
выполняется условие | ti | > t |
− |
α (ν) , то нулевая гипотеза отвергает- |
1 |
2 |
|
|
|
ся, то есть следует считать, что проверяемый коэффициент уравнения регрессии α*i существенно отличен от нуля или, что то же самое, контролируемая переменная xi оказывает значимое влияние
на переменную у.
Если последнее неравенство не выполняется, то переменная xi
влияет незначимо на переменную y. В этом случае уравнение регрессии нужно строить заново, учитывая в нем все переменные, кроме xi . Построение линейной регрессионной модели, у которой
все факторы xi существенно влияют на переменную у, может за-
кончиться не на первом, а на втором, третьем и т. д. этапе. На каждом из них заново проводится оценка коэффициентов регрессии и анализ влияния каждой переменной.
Если несмещенная оценка среднего квадратического отклонения Sε , вычисляемого по приведенной выше формуле, допустима для
данной задачи, то считаем, что модель хорошо согласуется с экспериментом. Обычно, в практических задачах требуют, чтобы Sε не
превышало 10% абсолютной величины наименьшего значения случайной величины η.
Если Sε велико, то модель регрессии нужно уточнить, то есть
взять большее число опытов и произвести все вычисления заново. Если и это не поможет, то можно сделать вывод о том, что выбран-
37

ная модель плохо согласуется с экспериментом. В этом случае нужно выбирать другой вид зависимости.
Пример. Произведено 10 измерений прочности строительного материала у при равном содержании в нем некоторых компонент ξ1,ξ2 . Заданные при проведении эксперимента значения x1 j , x2 j
компонент ξ1,ξ2 |
и полученные значения y j |
прочности η( j = |
1,10) |
|
|||||||||||
сведены в таблицу. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
1 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
|
|||
|
x1 |
0 |
1 |
|
2 |
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
|
|
|
x2 |
17,5 |
13,7 |
|
10,8 |
8,5 |
5,2 |
5 |
|
4,95 |
4,92 |
4,9 |
4,89 |
|
|
|
y |
13,25 |
15,95 |
|
17,63 |
18,63 |
19,2 |
19,37 |
|
19,5 |
19,6 |
19,67 |
19,7 |
|
|
Предполагая, что зависимость между величиной η и величинами ξ1,ξ2 линейная:
1)найти оценки a0 , a1, a2 параметров α*0 , α1*, α*2 уравнения регрессии;
2)найти 95%-e доверительные интервалы параметров α*0 , α1*, α*2 ;
3)проверить согласованность полученной модели регрессии с экспериментом.
Решение.
1.Для нахождения оценок a0 , a1, a2 коэффициентов выборочного
уравнения регрессии y = a0 + a1x1 + a2 x2 необходимо решить систе-
му алгебраических уравнений вида. Матрица коэффициентов X T X
этой системы и матрица-столбец свободных членов X TY записываются следующим образом:
|
n |
∑x1 |
|
∑x1 |
∑x12 |
X T X = |
||
|
∑x |
∑x x |
|
2 |
1 2 |
В нашем случае вычисления дают
∑x2
∑x1x2 ,
∑x22
|
∑y |
|
|
X TY = |
∑x1y . |
|
∑x2y |
38
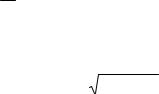
|
10 |
45 |
80,36 |
|
|
|
182,5 |
|
|
45 |
285 |
253,95 |
|
, |
|
869,61 |
|
X T X = |
|
X TY = |
. |
|||||
|
80,36 |
253,95 |
|
|
|
|
|
|
|
831,501 |
|
1381,512 |
|
||||
Решая систему (X T X )A = X TY линейных алгебраических уравнений третьего порядка, находим
a0 22,3634 A = a1 = −0,0473 .
a2 −0,4854
Значит, выборочное уравнение регрессии имеет вид
|
|
|
|
y = 22,3634 −0,0473x1 −0,4854x2 . |
(4.1) |
||
|
2. Прежде, чем находить доверительные интервалы параметров |
||||||
α* |
, α*, α* |
уравнения регрессии, убедимся, что |
остатки |
||||
0 |
1 |
2 |
|
|
|
|
|
εj |
= y j − |
|
( j = |
|
|
||
y j |
1, 10) распределены по нормальному закону. Так |
||||||
как число опытов мало, применим приближенный метод проверки. Для удобства вычислений составим таблицу
|
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
y j |
13,25 |
15,95 |
17,63 |
18,63 |
19,2 |
19,37 |
19,5 |
19,6 |
19,67 |
19,7 |
|
|
|
|
13,869 |
15,666 |
17,027 |
18,096 |
19,65 |
19,7 |
19,677 |
19,644 |
19,607 |
19,564 |
|
y j |
|||||||||||
|
εj |
−0,619 |
0,234 |
0,603 |
0,534 |
−0,45 |
−0,33 |
−0,177 |
−0,044 |
0,063 |
0,136 |
|
Значения y j вычисляются, исходя из уравнения регрессии (4.1).
|
n |
Используя данные таблицы, находим ∑ε2j =1,4805 . Средняя квад- |
|
|
j =1 |
ратическая |
ошибка Sε = 1,4805 / 7 = 0,4599 . Так как в интервал |
( − 2Sε,2Sε) |
попадают все остатки εj , то можно считать, что остат- |
ки распределены по нормальному закону.
39

Вэтомслучаедлянахождениядоверительныхинтерваловвычислим
диагональныеэлементы a |
(−1) |
, a(−1) |
, a(−1) матрицы ( X T X )−1 |
||||||||||||
|
|
|
|
|
11 |
22 |
|
33 |
|
|
|
|
|
||
det( X T X ) = |
|
10 |
|
|
|
45 |
|
80,36 |
|
= 37297,5 , |
|||||
|
|
|
|
|
|
||||||||||
|
45 |
|
|
|
285 |
|
253,95 |
|
|||||||
|
|
|
|
80,36 |
253,95 |
831,501 |
|
|
|||||||
a(−1) |
= |
1 |
|
|
|
|
285 |
|
253,95 |
|
= 4,6246 , |
||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
11 |
|
det( X T X ) |
|
253,95 |
831,501 |
|
|
|
|||||||
|
|
|
|
|
|
||||||||||
a22( −1) |
= |
1 |
|
|
|
|
10 |
80,36 |
|
= 0,0498 , |
|||||
|
|
|
|
|
|||||||||||
det( X T X ) |
|
80,36 831,501 |
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||
a33( −1) |
= |
1 |
|
|
|
|
10 |
45 |
|
= 0,0221. |
|
|
|||
|
|
|
|
|
|
|
|||||||||
det( X T X ) |
|
|
45 |
285 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
Далеенаходимсредниеквадратическиеошибкипараметров ai
Sa0 =Sε  a11(−1) =0,989, Sa1 =Sε
a11(−1) =0,989, Sa1 =Sε  a22(−1) =0,1026, Sa2 =Sε
a22(−1) =0,1026, Sa2 =Sε  a33(−1) =0,0684 .
a33(−1) =0,0684 .
По заданному уровню значимости α =1 − p =1 −0,95 = 0,05 и числу степенней свободы ν=n−m−1=7 находим критическое значение
t1−α2 (ν) = t0,975 (7) = 2,365 .
Доверительные интервалы параметров α*0 ,α1*,α*2 имеют вид
22,3634 − 2,365 0,989 < α*0 < 22,3634 + 2,365 0,989 ,
−0,0473 − 2,365 0,1026 < α1* < −0,0473 + 2,365 0,1026 ,
−0,4854 − 2,365 0,0684 < α*2 < −0,4854 + 2,365 0,0684 .
Окончательно получаем
20,024 < α*0 < 24,702 ; −0,289 < α1* < 0,195 ; −0,647 < α*2 < −324 .
40

Данные доверительные интервалы накрывают точные параметры α*0 , α1*, α*2 уравнения регрессии с вероятностью p =1 −α = 0,95 .
3. Так как остатки εj = y j − y j , ( j =1, 10) распределены по нормальному закону, то выявление статистически незначимых переменных, то есть проверку гипотезы H0 : α*i = 0 можно произвести с
помощью статистик ti = ai
Sai
t = |
0,0473 |
|
= 0,461 , t |
2 |
= |
0,4854 |
= 7,96 . |
|
|
|
|||||||
1 |
0,1026 |
|
|
|
0,0684 |
|
||
|
|
|
|
|
|
|||
Сравним полученные значения ti , i =1, 2 |
с критическим значением |
|||||||
t0,975 (7) = 2,365 . Видно, что |
полученное |
|
значение статистики t2 |
|||||
превосходит критическое значение, значит, коэффициент a2 отличен от нуля с вероятностью 0,95, то есть переменная x2 оказывает влияние на у. Значение t1 меньше критического, значит, коэффициент a1 незначимо отличается от нуля. Об этом свидетельствует и тот факт, что доверительный интервал для α1* накрывает нуль. Следовательно, переменная x1 незначимо влияет на у, и ее из выражения регрессии следует исключить.
Уравнение регрессии должно иметь вид η = β*0 +β*2ξ2 .
Для построения выборочного уравнения регрессии используем табличные значения x2 и у.
Пример. Задача ставится теперь так:
1)найти выборочный коэффициент корреляции и оценить его значимость;
2)построить уравнение регрессии y = b0* +b2*x2 и найти 95%-e до-
верительные интервалы параметров β*0 и β*2 .
Решение.
1.Так же, как и ранее, находим
ρ= −0,981,σx2 = 4,5427,σy = 2,1208, x22 = 83,1501.
41

Для проверки значимости коэффициента корреляции находим
tнабл.= |
0,981 8 |
≈14,29 . |
|
|
1 − (0,981)2 |
|
|
По уровню значимости |
α = 0,05 и |
числу степеней |
свободы |
ν = n − m −1 =10 −1 −1 =8 |
находим |
критическое |
значение |
tγ (ν) = t0,975 (8) = 2,306 , где γ =1 −α/ 2 =1 −0,05/ 2 = 0,975 .
Видно, что tнабл.> tγ(ν) . Значит, с вероятностью р = 0,95 можно утверждать, что ρ ≠ 0 , то есть случайные величины ξ2 и η не являются независимыми.
2. Находим оценки b0* и b2* коэффициентов β*0 и β*2 соответственно уравнения регрессии случайной величины η на ξ2
b0* = 21,9302, b2* = −0,458 .
Выборочное уравнение регрессии имеет вид: y = 21,9302 −0,458x2 . Находим 95%-е доверительные интервалы его коэффициентов
21,39302 −2,31 4,54272,1208 |
1−( − 0,981)8 |
2 83,1501 <β*0 < 21,9302 + 2,31 1,3397 , |
||||
−0,458 −2,31 |
2,1208 |
1−( − 0,981)2 |
* |
< −0,458 + 2,31 0,03202 , |
||
4,5427 |
8 |
<β2 |
||||
или, после преобразований, 18,836 < β*0 < 25,025 ; −0,5319 <β*2 < −0,384 .
42
