stat_2

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

yi = A + b(xi −

) + εi , i =1, 2, ..., n,

∑xi . То есть, фактически, мы ищем уравнения прямой

∑xi . То есть, фактически, мы ищем уравнения прямой

.pdf

Скачиваний:

Добавлен:

31.05.2015

Размер:

466.35 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Замечание 3. Широко распространенная в практических задачах ситуация, когда функция регрессии f (x,θ1,θ2 ,..., θk ) линейно зависит

от параметров θ1 ,θ2 ,...,θk , носит название линейного регрессионного

анализа. Например, f (x,a0 ,a1 , ..., ak ) = a0 + a1 x +... + ak xk . Замечание 4. Ситуация, в которой экспериментатор может

выбрать значения факторов xi по своему желанию и таким образом планировать будущие эксперименты, называется активным экспериментом. В этом случае значения факторов xi обычно рассматриваются как неслучайные. Более того, сообразуясь с целями эксперимента, экспериментатор может выбрать его план наилучшим образом (планирование эксперимента). В отличие от этой ситуации в пассивном эксперименте значения фактора складываются вне воли экспериментатора, под действием других обстоятельств. Поэтому значения xi приходится толковать как случайные величины, что накладывает особые черты на интерпретацию результатов. Сама же математическая обработка совокупности (xi, yi), i = 1, 2, ..., n от этого не меняется.

3.1. Анализ адекватности модели

После подбора регрессионной модели и нахождения ее параметров желательно выяснить, насколько хорошо выбранная модель описывает имеющиеся данные. К сожалению, общего правила для этого нет. На практике первое впечатление о правильности подобранной модели может дать изучение некоторых числовых характеристик, например, доверительных интервалов для оценок параметров модели. Однако эти показатели скорее позволяют отвергнуть совсем неудачную модель, чем подтвердить правильность выбора функциональной зависимости.

Более обоснованные решения можно принять, сравнив имеющиеся значения yi со значениями yˆi , полученными с помощью по-

добранной функции регрессии yˆi = f (xi ,θˆ) , то есть провести анализ остатков ri = yi − yˆi i =1, 2, ..., n .

Исследование остатков полезно начинать с изучения их графика, который может показать наличие какой-то зависимости, не учтенной в модели. Скажем, при подборе простой линейной зависимости между х и y график остатков может показать необходимость перехода к нелинейной модели (квадратичной, полиномиальной, экспоненциальной). Для проверки нормальности распределения остатков чаще всего используется график плотности нормального распределения или критерии хи-квадрат, Колмогорова и др.

3.2. Простейшая линейная регрессия

Проиллюстрируем изложенные выше идеи обработки регрессионного эксперимента на примере простой линейной регрессии. Допустим, что на первом этапе на основе анализа данных эксперимента, с учетом физических, экономических и других аспектов, а также из прошлого опыта мы выбрали в качестве модельного уравнения регрессии прямую линию

f (x, a,b) = a +bx ,

(3.1)

то есть в качестве модели регрессии между исследуемыми величинами Х и Y берется линейная зависимость Y = a +bX + ε. Тогда для данного xi соответствующее значение yi определяется равенством yi = a +bxi + εi , i =1, 2, ..., n . Здесь x1, x2, ..., xn – заданные числа

(значения фактора); y1, y2, ..., yn – наблюденные значения отклика,

ε1, ε2,…, εn – ошибки эксперимента, то есть некоторые значения независимых, одинаково распределенных случайных величин.

Кроме этого, далее мы будем рассматривать классическую модель регрессионного анализа, так называемую Гауссовскую модель, в которой дополнительно к вышесказанному предполагается, что

величины εi распределены по нормальному закону N (0;σ2 ) с неко-

торой неизвестной дисперсией σ2.

Отметим, что предложенный вид зависимости и сделанные предположения насчет распределения остатков εi – это модель, которой мы задаемся, но это не значит, что она верна на самом деле. Начав с предположения, что эта модель установлена, на последующих ста-

диях анализа мы будем проверять, так ли это на самом деле, то есть проверять адекватность модели реальному процессу, реальным данным, полученным в процессе наблюдения. Естественно, если факты будут против выбранной нами модели, то мы должны ее отклонить и попытаться разработать (выдвинуть) уже с учетом имеющейся информации другую модель и провести ее проверку.

На втором этапе анализа по результатам n экспериментальных данных (наблюдений) пары величин (X,Y): (x1, y1), (x2, y2),..., (xn,yn) мы должны оценить параметры выдвинутой нами модели. В случае прямолинейной регрессии это a и b.

Для более наглядной интерпретации результатов и некоторого упрощения расчетных формул немного преобразуем модельное уравнение регрессии, введя новый неизвестный параметр

A = a +b X . Уравнение (3.1) примет вид

f(x, A,b) = A +b(x − X ) ,

итогда предполагаемая связь между xi и yi запишется в виде

регрессии в форме y − y0 = k(x − x0 ) .

Таким образом, наша задача найти оценки параметров A и b:

ˆ	ˆ
α = A,	β =b , наилучшие в смысле метода наименьших квадратов.

Это вполне естественно, поскольку "истинная" линия регрессии, как мы упоминали выше, минимизирует математическое ожидание квадрата отклонения

[Y − f (X ,θ)]2 .

Теперь эмпирическое (выборочное) уравнение прямой регрессии Y на Х запишем в виде yˆ = α +β(x − X ) .

Левая часть равенства, которую мы обозначили yˆ , является оценкой (приближенным значением) математического ожидания M (Y)

при заданном значении x. Поэтому выборочные уравнения прямой регрессии Y на X записывается иногда в виде yˆx = α +β(x − X ) .

Полученное уравнение можно использовать как предсказывающее уравнение: подстановка в него значения x позволяет «предсказать» среднее значение Y для этого x. Если данные связаны идеальной линейной зависимостью (|rXY| = 1), то предсказанные значения Y будут в точности равняться наблюдаемому значению y при данном x. Однако, на практике обычно отсутствует идеальная линейная зависимость между данными, и внешние случайные воздействия приводят к разбросу данных. Тем не менее, если все же предположить существование линейной связи и наличие неограниченной выборки, то можно подобрать такие значения α и β, которые дадут возможность предсказать ожидаемое значение Y для любого значения x. Это означает, что yˆ не обязательно совпадает с наблю-

даемым значением Y, соответствующим данному x, однако оно будет равно среднему значению всех таких наблюдаемых значений.

Таким образом, на втором этапе исследования перед нами стоит задача: используя метод наименьших квадратов получить расчетные формулы для оценки параметров А и b прямолинейной регрессии.

Замечание. При изложении темы регрессионного анализа, как вы уже успели заметить, встает проблема в обозначениях: когда писать x или X, y или Y, и т.п. Как и ранее, когда речь идет о вычислительных процедурах, обработке данных, линиях регрессии, изучении функциональной зависимости мы, как правило, обозначаем перемен-

ные через x, y, yˆ , например, yˆ = α +β(x − x) . Если же нам надо провести статистический анализ этого соотношения, то мы его запи-

ˆ	ˆ	ˆ

сываем Y	= A +b( X − X ) , то есть речь идет о соотношении, свя-

зывающим случайные величины. При изложении материала мы не оговариваем каждый раз, какие обозначения применяются, но, надеемся, что из контекста это совершенно ясно.

3.3. Определение параметров прямолинейной регрессии методом наименьших квадратов

Суть метода наименьших квадратов состоит в том, что оценки ˆ

ˆ параметров А и b в предлагаемой линии регрессии и b

f (x, A,b) = A +b(x − x) подбирают таким образом, чтобы минимизировать сумму квадратов отклонений

n	n
S( A,b) = ∑εi2	= ∑[ yi − A −b(xi −	x	)]2 .
i=1	i=1

Данная функция принимает минимальное значение в точке, где обе частные производные обращаются в ноль:

			∂S	= 0,	∂S = 0 .
			∂A		∂b
После дифференцирования получим систему
		∂S = −2∑[ yi − A −b(xi − x)] = 0,
		∂A	n
		∂A	i=1
	∂S		n
	∂S	= −2∑(xi − x)[ yi − A −b(xi − x)] = 0.
	∂b	= −2∑(xi − x)[ yi − A −b(xi − x)] = 0.
	∂b		i=1

После несложных преобразований имеем систему двух линейных уравнений

An +b∑(xi

− x) = ∑yi ,

i=1

i−1

A∑(xi

−

) +b∑(xi

−

)2 = ∑(xi −

) yi ,

i=1

решение которой и даст искомые оценки A

и b :

1 n

∑(xi −

)( yi −

)

i=1

A = y =

∑yi ;

b =

n i=1

∑(xi

−

i=1

Полученные оценки обладают следующими важными свойствами:

1.	ˆ		ˆ
	M ( A) = A, M (b) = b .
2.	ˆ	2	ˆ	2	n	2	−1

	D(A) = σ		/ n, D(b) = σ		∑(xi − x)		.
3.	C(A,b) = 0 .				i=1

ˆˆ

4.Случайныевеличины A и b распределеныпонормальномузакону.

ˆˆ

5.A и b независимы как случайные величины.

Доказательства утверждений 1–3 могут быть получены прямыми

вычислениями, причем эти свойства не используют предположения о нормальном характере ошибок. Свойство 4 верно только в рассматриваемой нами Гауссовской модели. Свойство 5 есть естест-

венное следствие нормальности ошибок и свойства 3.

Независимостьоценок A и b заметноупрощаетдальнейшийанализ.

Замечание 1. Полученные формулы для оценок A

и b легко пре-

образовать к виду, более удобному для вычислений и анализа:

−

A = y =

∑yi ,

b =

σx2

, где x =

∑xi ,

y =

∑yi ,

n i=1

)2 = x2 −(

)2.

∑xi yi ,

σ2x =

∑xi2 − (

n i=1

Замечание 2. Уравнение регрессии Y на X записывается в виде

ˆ = + ˆ − y y b(x x).

Если X и Y – случайные величины, то, поменяв в наших выкладках местами X и Y, получим прямую регрессии X на Y

( y − y).

xˆ = x +b1

∑yi2

xy − x y

i=1

где

σy

σy =

−

(y)

= y

−(y).

Заметим, что обе прямые регрессии проходят через точку (x, y) . Угловые коэффициенты наклона прямых связаны с выборочным ко-

эффициентом корреляции соотношением rXY =					ˆ	ˆ	. Если, кроме
эффициентом корреляции соотношением rXY =					b	b1	. Если, кроме
	ˆ		2				ˆ
	b		σx				ˆ
этого, учесть		=	2	, то можно получить выражение для оценок b
этого, учесть	ˆ	=	2	, то можно получить выражение для оценок b
	b1		σy

ˆ	через выборочный коэффициент корреляции и выборочные
и b1
	ˆ		σy			ˆ		σx
дисперсии b		=			rXY ,	b1	=	σ		rXY .
			σ	x					y

Часто эти оценки называют выборочными коэффициентами регрессии Y на X и X на Y соответственно и обозначают ρY / X и ρ X / Y ,

то есть
ˆ		σy			ˆ		σx
ρY / X = b	=			rXY ,	ρ X / Y = b1	=	σ		rXY .
ρY / X = b	=	σ	x	rXY ,	ρ X / Y = b1	=	σ	y	rXY .
			x					y

Замечание 3. Легко увидеть, что прямые регрессии Y на X и X на Y совпадают только в том случае, когда | rXY |=1, то есть X и Y связаны линейной зависимостью. Действительно, оба уравнения в

этом случае преобразовываются к виду y − y = x − x .

σy σx

3.4. Доверительные интервалы для параметров линейной регрессии

ˆ		ˆ
Свойства 1–4 оценок A	и b параметров линейной регрессии по-
казывают, что случайные величины			ˆ		ˆ	распределены по нор-
казывают, что случайные величины			A	и b		распределены по нор-

	ˆ		σ2		ˆ		σ2
			σ2				σ2

мальному закону, причем	A N A,		n	, b N b,			n			, где
			n				∑(xi −	x	)2
							i=1

ˆ = σ2 = σ2

D( A) ˆ

A n

ˆ	2		σ2		ˆ	ˆ
, D(b) = σˆ		=		,	M ( A) = A,	M (b) = b .
, D(b) = σˆ		=	n	,	M ( A) = A,	M (b) = b .
	b		n
			∑(xi − x)2

i=1

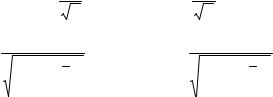
Этот факт дает возможность применить к построению доверительных интервалов ту же методику, что и при построении доверительных интервалов для неизвестного математического ожидания в главе 1.

1. Если дисперсия ошибок эксперимента σ2 известна (что бывает крайне редко, и этот случай представляет собой больше теоретический интерес), то рассматриваем случайные величины

	ˆ			ˆ	−b
u ˆ =	A − A	,	u ˆ =	b		,

A	σ ˆ		b	σˆ
	A				b

которые имеют нормальное распределение N(0;1). Для данного уровня значимости α получаем P(| u |< u1−α/ 2 ) =1−α. Из последнего соотношения находится u1−α/ 2 – квантиль нормального распреде-

ления, тогда

ˆ	,	ˆ	−b \| < u	.
\| A − A \| < u	,	\| b	−b \| < u	.
1−α/ 2			1−α/ 2
σ ˆ		σˆ
A			b

При этом доверительные интервалы будут следующими:

		ˆ		σ	ˆ	σ
		A −		n u1−α/ 2	< A < A +	n u1−α/ 2		,
ˆ	−	σ		u1−α/ 2	ˆ	σ		u1−α/ 2 .
b	−	n		u1−α/ 2	< b < b +	n		u1−α/ 2 .
		n	− x)2			n	− x)2
		∑(xi	− x)2			∑(xi	− x)2
		i=1				i=1
2. Пусть теперь σ2				– неизвестна, что чаще всего бывает на прак-

тике. В таком случае естественно воспользоваться какой-то оценкой σˆ 2 . Ключ к оцениванию σ2 дает остаточная сумма квадратов

ε2

= n

− ˆ

2 = n

−

ˆ − ˆ

−

[yi

x)]

∑ i

∑( yi

yi )

∑

A b(xi

i=1

Можно доказать, что в рассматриваемой нами Гауссовской модели

ˆ	ˆ	σ	2	2	, где
эта сумма не зависит от A	и b , и имеет распределение	σ		χn−2	, где

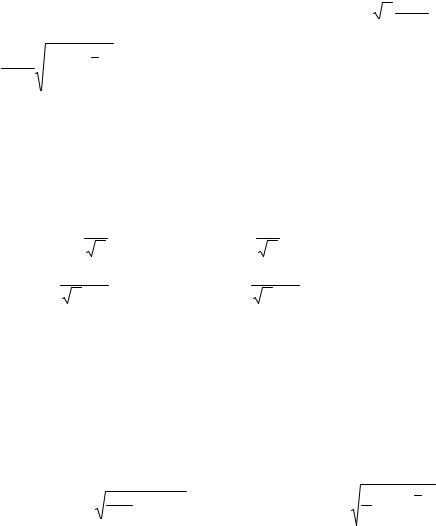
χ2n−2 – распределение хи-квадрат с n – 2 степенями свободы. Благодаря этому свойству для σ2 можно построить несмещенную оценку Syx :

)] .

Syx =

i∑=1[yi − A −b(xi −

n − 2

не зависит от

A−A

Поскольку Syx

A и b , то статистики t ˆ

Syx

−b

−x)2

имеют распределение Стьюдента с n − 2 степе-

∑(x

Syx

i=1

нями свободы. Тогда для данного уровня значимости α и по числу

степеней	свободы n − 2 по				таблицам		квантилей	распределения
Стьюдента находим квантиль порядка 1 − α , то есть t									/ 2	(n −2) .
					ˆ	ˆ	2	1−α	/ 2
					ˆ	ˆ	запишутся в той же фор-
Доверительные интервалы для A и						b	запишутся в той же фор-
ме, что и при известном σ2 :
	ˆ		Syx		ˆ		Syx
	A −		n t1−α/ 2	(n − 2)	< A < A +		n t1−α/ 2 (n − 2) ,
ˆ		Syx			ˆ		Syx
b	−	n σx t1−α/ 2		(n − 2)	< b < b	+	n σx t1−α/ 2	(n − 2) .

Замечание. Полученные выражения для доверительных интервалов можно записать в другой форме. Путем несложных преобра-

σy

зований, с учетом того, что b =

rXY

A = y , остаточная сумма

квадратов запишется в виде

n ε2

= n

− ˆ

2 = n

−

ˆ −

−

2 =

σ2

−

x)]

) .

∑ i

∑( yi

yi )

∑[yi

b(xi

y (1

rXY

i=1

Тогда S yx = σy

(1−rXY2

) . Крометого, таккак σx=

1 ∑(xi−x)2 ,

n−2

n i=1

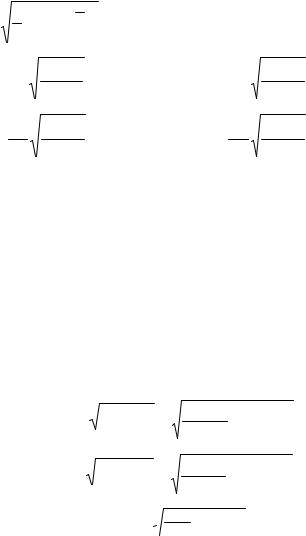
	1	n	− y)2 , тодоверительныеинтервалыимеютвид:
σy =
		∑( yi
	n i=1

ˆ		1 − r2
ˆ		XY
A −σy		n − 2
		n − 2
ˆ	σy	1 − r2
b	− σx	n − 2

ˆ		1 − r2
ˆ		XY	t1−α/ 2 (n − 2) ,
t1−α/ 2 (n − 2) < A < A + σy		n − 2	t1−α/ 2 (n − 2) ,	(3.2)
ˆ	σy	1 − r2
t1−α/ 2 (n − 2) < b < b	+ σx	n − 2	t1−α/ 2 (n − 2) .	(3.3)

Последние формулы наиболее удобны для вычислений.

Пример. Определить по данным, приведенным в п. 1.5, прямую регрессии, задающую линейный прогноз средней массы студента по его росту. Найти 95%-й доверительный интервал для параметров прямой регрессии.

Решение. С учетом вычислений, проделанных в п. 1.5., имеем,

ˆ	ˆ	344493 − 25 179,4 76,64

что при n = 25, α = 0,05: A=y=76,64,	b=		=0,51 .
		806105 − 25 179,42

Следовательно, прямая регрессии, оценивающая среднюю массу студента по его росту, имеет вид yˆ = 76,64 + 0,51 (x −179,4) .

Дляпостроениядоверительныхинтерваловоценок A и b вычислим

−(

806105

−(179,4)2

σx =

= 7,736 ,

−(

148918

−(76,64)2

σy =

= 9,1121 ,

Syx = σy n−n2 (1 − rXY2 ) = 8,5763 .

Квантиль распределения Стьюдента с числом степеней свободы n − 2 = 23, порядка 1− α2 равна t0,975 (23) = 2,069 .

После подстановки в формулы (3.2) и (3.3) получим доверитель-

ные интервалы 73,0899 < A < 80,190, 0,0511 < b < 0,9689.

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.09.2019156.67 Кб10STATIKA.doc
#
31.05.2015398.34 Кб48Statistika МЕТОДИЧКА.doc
#
21.09.20191.06 Mб0STATISTIKA.doc
#
31.05.2015596.48 Кб18Statistika_-_zachyot-_gotovye_shpory.doc
#
31.05.2015774.61 Кб25stat_1.pdf
#
31.05.2015466.35 Кб15stat_2.pdf
#
31.05.20151.1 Mб134STM32f407 AD9248.docx
#
31.05.2015211.92 Кб24strategic_mgmnt_kr.docx
#
10.11.2019334.34 Кб43stroit.materialovedenie.doc
#
31.05.20151.54 Mб101stroitelnie_materialy.doc
#
31.05.2015215.04 Кб44stroitelnye_materialy_75_voprosov.doc