Уравнения состояния

Математическая модель может быть представлена в виде структурной схемы. Уравнение состояния – это те же дифференциальные уравнения только записанные в форме Коши. Уравнения состояния имеют вид:

Y=CX;

X – вектор состояний объекта U– вектор управления

Y– вектор выходных координат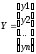

A,B,C– матрицы коэффициентов;

Перемножим матрицы и получим:

ЭЛ. двиг. пост. тока как объект автоматического управления

Схема замещения эл. двиг. пост. тока

U – напряжение на якоре

I– ток на якоре

R – активное сопротивление якорной цепи

L– индуктивность якорной цепи

e– противо ЭДС двигателя; Ф=const – магнитный поток

Управление двигателем осуществляется за счёт напряжения на якоре.

Согл. 2-му з.Кирхгофа

Это уравнение дополним основным уравнением движения электропривода

, где J – момент инерции приведённый к валу двигателя.

М и М_с– соответственно полный и статический момент электродвигателя.

Преобразуем уравнения по Лапласу

- при постоянном магнитном потоке.

e=c_eω, гдеc_e – конструктивная постоянная. Если расчёты ведутся в системе СИ, тоc_e иc_мотличаются на 2%, тогда принимаемc_e=c_м

Общепринято за выход брать не скорость, а противоЭДС е

_{Домножим последнее уравнение на} R_яци разделим на с_е: _{(1), где - электромеханическая постоянная времени. Она характеризует механическую инерционность, при мгновенном изменении тока (момента) скорость мгновенно измениться не может.}

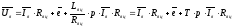_{(2), где - электромагнитная постоянная времени. Характеризует электромагнитную инерционность, т.е. при мгновенном изменении напряжения на якоре за счёт Lяц ток мгновенно изменится не может.}

_{На основании (1) и (2) можно составить структурную схему, т.е. математическую модель эл.двиг. для изображения сигналов.}

_{Из (1) следует, что}

_{Ток определяется нагрузкой в установившемся режиме:}

_{На основании данной структурной схемы можно записать передаточную функцию по возмущающему воздействию.}

_{В зависимости от Tm и T звено может быть колебательное или апериодическое.}

Если 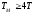, то звено колебательное, а если, то звено апериодическое.

Статические свойства САУ

САУ должна обладать необходимыми статическими и динамическими свойствами. Статические свойства системы определяются статической характеристикой F

Uз y

Статической характеристикой системы называется зависимость выходной величины САУ от возмущающего воздействия при различных значениях задающего сигнала.

Статическая характеристика линейной системы также линейна.

Статическое свойство численно характеризуется понятием статизма

Ун—Номинальное значение выходной координаты при номинальном значении возмущающего воздействия

Пример. Номинальная частота вращения двигателя при номинальном токе.

заданное значение выходной координаты

S1-Статизм по заданиюS2- Статизм по возмущению.

На практике часто пользуются понятием как статизм характеристики

Статическая характеристика имеет жёсткую связь со статической по возмущению и характеризует наклон статической характеристики. При проектировании систем необходимо что бы Sx<Sxнеобх. при заданном диапазоне регулированияD. Диапазон регулирования отношение максимального значения выходной координаты к минимальному значению.

Чем меньше Sxтем система более качественна.

С точки зрения статики все системы делятся на статические и Астатические. В статических системах Sx>0

В астатической системе Sx=0

В настоящее время преобладает большинство систем астатических.

По структурной схеме можно записать уравнение для статической

характеристики, необходимо положить что р=0

Отличным примером астатической системы является наличие в канале

главной ошибки астатического звена.

Главной ошибкой называется разность между задающим сигналом и сигналом обратной связи по выходной координате.

С точки зрения статики звенья делятся на статические и астатические.

По первой функции можно определить вид звена. Для астатического звена функция имеет вид.

Xвх Хвых

1/Tp

Пример: Пусть имеется система

Uз=5

F=5

α=0,2

γ=0,2

Построим выходную характеристику и определим величину статизма

Устойчивость САУ. Критерии устойчивости линейных САУ.

Для исследования устойчивости линейной системы достаточно найти корни ее характеристического полинома. Если все корни имеют отрицательные вещественные части (находятся в левой полуплоскости, слева от мнимой оси), такой полином называется устойчивым, потому что соответствующая линейная система устойчива. Полиномы, имеющие хотя бы один корень с положительной вещественной частью (в правой полуплоскости) называются неустойчивыми.

Устойчивость это свойство системы самостоятельно переходить к последующему установившемуся значению ,после приложения входного воздействия , которое вывела систему из состояния равновесия

С точки зрения устойчивости системы бывают

1. Устойчивые

2. На границе устойчивости

3. Неустойчивые

Устойчивость это свойство системы , которое не зависит от формы входного воздействия и точки приложения его в системе или другими словами нельзя подобрать такой закон изменения входного воздействия чтобы сделать из неустойчивой системы устойчивую

Критерии устойчивости сау

Определять по корням устойчивость системы неудобно (1,2- порядок)

Выше 4ого порядка нельзя найти корни, поэтому существует ряд критериев , позволяющих определить устойчивость Сау без нахождения корней характеристического уравнения

Все критерии делятся на

1 алгебраические (рауса гурвица)

2 частотные (найквиста,михайлова)

Критерий Гурвица.

Гурвиц предложил другой критерий устойчивости. Из коэффициентов характеристического уравнения строится определитель Гурвица по алгоритму:

1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a₁до a_n;

2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;

3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули.

Чтобы система была устойчива, необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и все n главных диагональных миноров матрицы Гурвица были положительны. Число определителей Гурвица равно порядку характеристического уравнения п.

Критерий Гурвица применяют при n ≤ 5. При больших порядках возрастает число определителей, и процесс становится трудоемким. Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ.

Критерий устойчивости Найквиста. Этот критерий основан на связи свойства устойчивости замкнутой системы с формой АФЧХ разомкнутой устойчивой системы. Разомкнутой системой являются все последовательно соединенные блоки от входа системы до точки замыкания обратной связи (рис. 4.2.3). Исследование разомкнутой системы проще, чем замкнутой, и его можно производить экспериментально.

W(p)-ПФ в разомкнутой системе по выходной координате

Согласно правилу преобразования стр. схем ПФ заменим систему

Тогда характеристическое уравнение имеет вид:

Где p_i –корни характеристического уравнения замкнутой системы А(р)+В(р)=0

s_i -корни характеристического уравнения разомкнутой системы А(р)=0

p=jω мы получаем:

Число корней замкнутой системы равно числу корней разомкнутой системы, т.к. B(p)≤A(p) (порядок)

Исходим из того что разомкнутая и замкнутая система устойчивы(на практике как правило разомкнутая система устойчива)

Замечксел по выходной координате чтобы улучшить статические свойства системы

Система III кор.:

Пусть P₁-R₂, а Р₂,Р₃-комплексно сопряженные p₁=-δ₂±jω₂

Вектор jω-p₁, при ω=0

jω-p₂

jω-p₃

При ω от 0 до ∞ jω-p_, повернется на , то есть в сумме все угла,

, где n порядок характеристического уравнения 0₁, тоже с в-рами ) итд: они повернутся на угол

Суммарный угол поворота 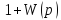в устойчивой системе при от 0 до∞ будет равен 0

Если система неустойчива то для действующих корней угол поворота будет - и суммарный угол поворота не будет =0

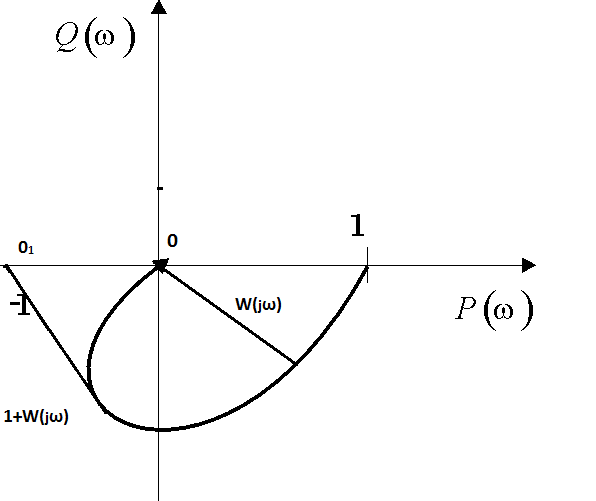
То есть условие устойчивости по Найквисту формулируется следующим образом:

Замкнутая система устойчива, если устойчива разомкнутая и её АФЧХ при изменении ω от 0 до ∞ не охватывая точку с координатами (-1;j0)

По АФЧХ разомкнутой системы можно определить запас устойчивости системы по амплитуде и по фазе- проводим окружность единичного радиуса

- запас устойчивости по фазе

- зепас устойчивости по амплитуде

Если система устойчива, то при повороте W(jω) амплитуда <1 (φ=-π)

Система устойчива, если А(ω)<1 при φ=-π

Система неустойчива, если А(ω)>1 при φ=-π

Система устойчива, если А(ω)=1 при |φ(ω) |<π

Система неустойчива, если А(ω)=1 при |φ(ω) |>π

Устойчивость можно определить по ЛАХ устойчивых систем

Система устойчива: φ(ω)= -π

L(ω)<0

Т₀=0,01с; T= 0,04c; Т_M=0,1с; α=0,02; β=50

Для определения устойчивости нет необходимости полностью стоить АФЧХ по точкам, нам достаточно определить точки пересечения с осью абсцисс (то есть определить положения Т=1).

от сюда следует что

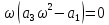
Система устойчива (так как Т -1 исходная за перечисления)