8. Математическая статистика

8.1. Выборочный метод. Статистическое распределение

выборки. Эмпирическая функция распределения

Изучение всего набора элементов генеральной совокупности часто оказывается невозможным из-за больших материальных затрат или бесконечности генеральной совокупности. В этом случае применяется выборочный метод. Сущность выборочного метода заключается в том, что из генеральной совокупности извлекается выборка. На выборке производят нужные исследования, а полученные результаты распространяют на всю совокупность.

Пусть для изучения количественного признака Х из генеральной совокупности извлечена выборка объемаn. Наблюдаемые значения х_i признака Х называют вариантами, а последовательность вариантов, записанную в возрастающем порядке, – вариационным рядом. Статистическим распределением выборки называется перечень х_i и соответствующих им частот т_i или относительных частот _i.

Статистическое распределение выборочной совокупности можно представить графически в виде полигона или гистограммы. Полигоном частот выборочной совокупности называется ломаная линия, соединяющая точки с координатами .

Гистограммой выборочной совокупности называется фигура, составленная в декартовой системе координат из прямоугольников, основаниями которых являются частичные интервалы , а высоты соответственно равны, где.

Эмпирической функцией распределения называется функция , гдеn_х – число вариант в выборке, меньших х; п – объем выборки. Эмпирическая функция распределения при больших п служит оценкой неизвестной функции распределения генеральной совокупности. Эмпирическая функция распределения обладает следующими свойствами:

1) ;

2) эмпирическая функция распределения является неубывающей функцией, т. е. если , то;

3) если – наименьшая варианта, а– наибольшая варианта, топриипри.

8.2. Точечные оценки неизвестных параметров распределения

Статистической оценкой неизвестного параметра генеральной совокупности называется функция от наблюдаемых значений случайной величины Х. Сами наблюдаемые значения (варианты) рассматриваются как значенияп независимых СВ , имеющих тот же закон распределения, что и изучаемая СВХ. Поэтому статистические оценки также являются случайными величинами.

Статистическая оценка называется точечной, если она определяется одной величиной. Точечная оценка, математическое ожидание которой равно оцениваемому параметру, называется несмещенной, в противном случае – смещенной.

Несмещенной оценкой для математического ожидания генеральной совокупности является – выборочная средняя:

.

Смещенной оценкой для дисперсии генеральной совокупности является выборочная дисперсия , а несмещенной оценкой для дисперсии генеральной совокупности является исправленная выборочная дисперсия.

,

,

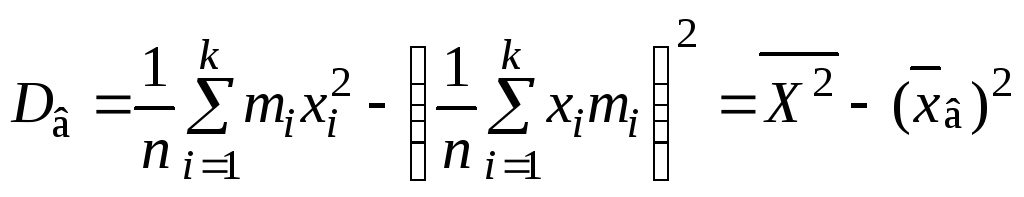Оценка параметра называется состоятельной, если она сходится по вероятности к оцениваемому параметру при неограниченном числе испытаний, т. е. для любого сколь угодно малого  > 0 выполнено предельное равенство .

Один и тот же параметр может иметь несколько оценок, которые обладают различными дисперсиями при ограниченном числе опытов. Чем меньше эта дисперсия, тем меньше вероятность совершить ошибку при оценке параметра. Поэтому в качестве оценки берется та, которая обладает минимальной дисперсией (эффективная).