УП часть 2 ТА

Ю. С. Акинина, C.В. Тюрин

ЭЛЕМЕНТЫ ТЕОРИИ АВТОМАТОВ (Часть II)

Учебное пособие

Воронеж 2012

УДК 519.713 (075)

Акинина Ю.С., Тюрин С.В.Элементы теории автоматов (Часть II). Учеб. пособие. Воронеж: Воронеж. гос. техн. ун-т, 2012. 84 с.

Рассматриваются вопросы, касающиеся различных цифровых устройств. Большое внимание уделено теоретическим основам комбинационных устройств, способам их описания, принципам построения структурных формул и методам их минимизации, принципам построения логических схем. На основе этого материала рассмотрены типовые комбинационные устройства: шифраторы, дешифраторы, мультиплексоры, демультиплексоры.

Освещены вопросы программируемых логических интегральных схем. Изложены принципы построения и функционирования некоторых последовательностных устройств.

Учебное пособие предназначено для студентов технических вузов, обучающихся по специальности 230101 "Вычислительные машины, комплексы, системы и сети".

Табл. 30. Ил. 34. Библиогр.: 14 назв.

Научный редактор д-р техн. наук С.Л. Подвальный

Рецензенты: кафедра информатики и вычислительной техники Международного института компъютерных технологий.

к. т. н. Олейникова С.А.;

Печатается по решению редакционно-издательского совета Воронежского государственного технического университета.

©Акинина Ю.С., Тюрин С.В., 2012

©Оформление. Издательство Воронежского государственного технического университета, 2012

1. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ

Целью минимизации логических функций является получение более простых аналитических выражений, что в свою очередь позволяет осуществлять более простую минимизацию синтезируемого автомата.

Для рассмотрения вопроса минимизации необходимо сформулировать следующие определения.

Совершенной дизъюнктивной нормальной формой (СДНФ)

логической функции f (x1,..., xn ) называется дизъюнкция

элементарных конъюнкций максимального ранга (n), соответствующих наборам всех входных переменных, на которых значение логической функции равно 1.

Дизъюнктивной нормальной формой (ДНФ) логической

функции f (x1,..., xn ) называется дизъюнкция элементарных конъюнкций функции, ранг хотя бы одной из которых меньше

конъюнкций, ранг хотя бы одной из которых меньше максимального ранга (n) и которые не могут быть более склеены (т.е. объединены) между собой. Такие элементарные конъюнкции принято называть

импликантами.

Тупиковой дизъюнктивной нормальной формой логической функции f (x1,..., xn ) называется такая ДНФ, реализующая

f (x1,..., xn ) , в которой ни одна из импликант не является лишней, то есть ни одна из импликант не может быть удалена из

реализующая f (x1,..., xn ) , в которой количество импликант минимально по сравнению с другими ДНФ, реализующими

букв переменных по сравнению с другими ДНФ, реализующими функцию f (x1,..., xn ) .

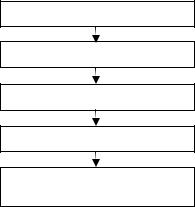
Общую схему минимизации логических функций можно проиллюстрировать следующим образом:

Исходная таблица истинности

СДНФ логической функции

Сокращенная ДНФ функции

Тупиковая ДНФ функции

Кратчайшая и минимальная ДНФ функции

Задача минимизации логических функций осложнена

величиной 23n . Число “3” определяется тем, что возможны три исхода: любая логическая переменная может входить в ДНФ со значением инверсии, без знака инверсии, может не входить в

мощность множества D, состоящего из объектов ДНФ логической функции f (x1,..., xn ) [1].

2.Среди множества D содержится одна единственная

СДНФ логической функции f (x1,..., xn ) и некоторое количество тождественных ей сокращенных и тупиковых ДНФ, реализующих

функцию f (x1,..., xn ) . В настоящее время не существует какого-

либо способа определения общего количества тождественных ДНФ, реализующих одну и ту же логическую функцию.

3. Вид тождественной ДНФ логической функции существенно зависит от формы записи СДНФ и порядка преобразований, производимых над СДНФ логической функции.

Все известные на сегодня способы минимизации логических функций могут быть поделены на 2 большие группы:

1.Методы минимизации одновыходных логических

функций.

2.Методы минимизации системы логических функций, зависящих от n-аргументов.

Среди методов первой группы выделяют следующие методы: прямые преобразования логических функций, визуальные методы минимизации с помощью специальных таблиц, машинноориентированные методы минимизации.

Все методы минимизации одновыходных логических функций базируются на следующих операциях:

3.a × K1 + a × K 2 = a × K1 + a × K 2 + K1 K 2 - обобщенное

склеивание.

4. K1 × K 2 + K1 = K1 - поглощение.

1.1 Методы минимизации логических функций на основе прямых преобразований СДНФ

Одним из первых таких строго формализованных методов является метод Квайна. Сущность этого метода состоит в следующем: если над исходной СДНФ произвести сначала все возможные операции неполного склеивания, а затем над полученным выражением все возможные операции поглощения, то в результате выполненных преобразований будет получена сокращенная ДНФ.

Проиллюстрируем применение метода Квайна для минимизации логической функции F(a,b,c) , заданной следующей

таблицей истинности (табл. 1.1):

Таблица 1.1

Выпишем СДНФ функции F(a,b,c) :

Пронумеруем каждую конъюнкцию из (1.1) следующим образом:

Затем, склеиваем (если это возможно) каждый из членов выражения (1.2) с последующими членами это выражения и

записываем полученные импликанты так, как показано в таблице

1.2.:

Таблица 1.2

Соединяя полученные импликанты знаками дизъюнкции, получаем сокращенную ДНФ логической функции F (a,b,c) :

Используя метод Квайна для минимизации логических функций необходимо помнить о том, что в этом методе используется операция неполного склеивания. Если в СДНФ, реализующей логическую функцию, присутствует конъюнкция, которая не может быть склеена ни с одной последующей

конъюнкцией, то эта конъюнкция должна быть включена в полученную в результате минимизации сокращенную ДНФ.

1.2 Метод испытания импликант

После получения сокращенной ДНФ, к ней может быть многократно применен метод Квайна, в результате чего будет получена некоторая тупиковая форма тождественная исходной ДНФ. Более часто применяют другой метод: метод испытания импликант в сокращенной ДНФ логической функции.

Существо метода состоит в следующем: из формулы, являющейся сокращенной ДНФ, выбирается испытываемая импликанта (можно произвольным образом). Выбранная импликанта приравнивается к 1. Далее определяются значения логических переменных, обращающих в 1 испытываемую импликанту. Из сокращенной ДНФ удаляется испытываемая импликанта, а в оставшуюся часть сокращенной ДНФ подставляются найденные значения логических переменных, обращающих в 1 испытываемую импликанту. Если в результате такой подстановки значение логической функции равно единичному значению, то испытываемая импликанта является лишней (избыточной) и может быть удалена из сокращенной ДНФ логической функции. После удаления лишней импликанты также испытываются все импликанты, входящие в сокращенную ДНФ.

Рассмотрим метод испытания импликант на примере.

Пусть логическая функция F(a,b,c) , представлена в виде

Испытаем импликанты в (1.3). Первой будем испытывать импликанту ab .

Импликанта ab обращается в 1 при следующих значениях логических переменных:

1.ab =1, при a =0, b =0. Подставляя найденные значения

в(1.3), предварительно исключив из формулы испытываемую импликанту, получим:

1× c +1× c + 0 × c + 0 × c + 0 × 0 = 1 Þ импликанта ab является

лишней и должна быть удалена из формулы.

Таким же образом испытаем оставшиеся в формуле импликанты.

2. ac =1, при a =0, c =0.

b × 0 + b ×1 + 0 × 0 + 0 × b = b Þ импликанта ac не является лишней. Оставляем ее в формуле.

3. bc = 1, при b =0, c =1.

a × 0 + 0 × 0 +1× c + a × 0 = c Þ импликанта bc не является лишней. Оставляем ее в формуле.

4. bc =1, при b =1, c =0.

Оставляем ее в формуле.

После испытания импликант получаем одну из тупиковых ДНФ логической функции F (a,b,c) :

Если начать испытание импликант в (1.3) не с первой импликанты, а с какой-либо другой, выбранной произвольным образом, то можно получить некоторое количество тождественных сокращенных и тупиковых ДНФ, реализующих