2.2. Дифференциальные уравнения гидростатики

2.2.1. Дифференциальные уравнения равновесия жидкости

Эйлера

2.2.2. Основное дифференциальное уравнение гидростатики

2.2.3. Дифференциальное уравнение поверхности

2.2.1. Дифференциальные уравнения

равновесия жидкости Эйлера

Рассмотрим состояние равновесия жидкости в общем случае, т.е. когда на неё действует сила тяжести и сила инерции переносного движения при относительном покое.

Выделим в покоящейся жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными координатным осям и соответственно равным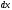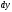и , и 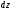(рис. 2.6).

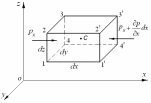
Рис. 2.6. Схема для вывода дифференциальных

уравнений равновесия жидкости

Введём обозначения:

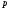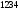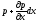- среднее гидростатическое давление на площадку ;

- среднее гидростатическое давление на площадку ;

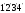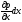- дифференциал, который выражает изменение давления от точки к точке вдоль оси 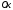при расстоянии между точками;

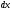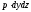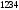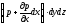- сила гидростатического давления на площадку ;

- сила гидростатического давления на площадку ;

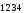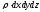- масса параллелепипеда;

- проекции ускорений единичной массовой силы;

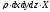- проекция единичной массовой силы на ось .

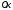На параллелепипед действуют силы гидростатического давления от окружающей жидкости и массовые силы.

Запишем уравнение равновесия в направлении оси

.

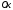
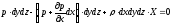После преобразования и деления на 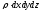уравнение примет вид

,

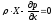или

.

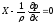Аналогичным образом получим уравнения в направлении осе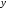й и:

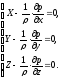(уравнения Эйлера) (2.8)

Полученная система уравнений равновесия жидкости называется уравнениями Эйлер. Они выведены Л.Эйлером в 1755 г.

Слагаемые, входящие в полученные уравнения, являются проекциями единичных массовых и поверхностных сил. Эти уравнения показывают, что поверхностные и массовые силы, действующие на жидкость, взаимно уравновешиваются.

2.2.2. Основное дифференциальное уравнение гидростатики

На практике удобнее пользоваться не системой уравнений, а одним уравнением, не содержащим частных производных. Умножим каждое уравнение (2.8), соответственно, на 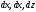и, сложив их, получим

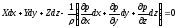. (2.9)

Трехчлен, заключенный в скобки, представляет собой полный дифференциал давления 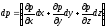, т.е. приращение давления при изменении координат на величины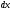, 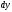и .

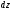Следовательно, можно записать

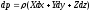. (2.10)

Уравнение (2.10) называется основным дифференциальным уравнением гидростатики. В таком виде дифференциальное уравнение Эйлера обычно применяется на практике в общем случае равновесия жидкости.

Отступление: Л. Эйлер (1707—1783 гг.) - известный математик, механик и физик. Родился и получил образование в Базеле (Швейцария). Свыше 30 лет прожил в Петербурге, работая в Петербургской академии наук. Помимо математики, физики, теории упругости, теории машин и других наук занимался гидромеханикой, вывел дифференциальные уравнения движения жидкостей и газов, предложил критерий гидродинамического подобия. Считается одним из основоположников гидромеханики.

2.2.3. Дифференциальное уравнение поверхности

Поверхностью уровня, или поверхностью равного давления, называется геометрическое место точек, испытывающих в жидкости одинаковое давление. В каждом частном случае равновесия существует множество поверхностей уровня, одна из которых совпадает со свободной поверхностью жидкости.

По определению, каждая поверхность уровня характеризуется условием

; .

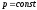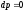Подставляя это условие в основное уравнение гидростатики (2.10), получим

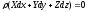. (2.11)

Так как массовая плотность не может быть равной нулю, то

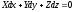. (2.12)

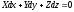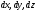Это и есть уравнение семейства поверхностей уровня в самом общем случае равновесия жидкости. Каждое из трёх слагаемых в левой части этого уравнения можно представить как работу единичной массовой силы на элементарном пути в направлении данной оси координат, а весь трехчлен - как работу результирующей единичных массовых сил на элементарном приращении путивдоль поверхности уровня. Как видно из (2.12), эта работа оказывается равной нулю. Следовательно, результирующая массовых сил направлена по нормали к поверхности уровня в каждой данной её точке.

Справедливость этого заключения ясна и из чисто логического рассуждения: если бы результирующая сила не была нормальной к поверхности уровня, то существовала бы её тангенциальная составляющая, которая производила бы сдвиг жидкости, а, следовательно, равновесия не существовало бы.

Разумеется, уравнения (2.10) и (2.12) в общем случае интегрированию не поддаются. Их решение зависит от граничных условий каждого частного случая равновесия.