
- •Г.И. Скоморохов
- •Введение
- •Основные физические свойства жидкостей
- •1.1. Определение жидкости
- •1.2. Классификация сил, действующих в жидкости
- •1.3. Основные физические свойства жидкостей
- •Гидростатика
- •2.1. Основные понятия гидростатики
- •2.1.2. Давление абсолютное, избыточное, вакуум
- •2.1.3. Свойства гидростатического давления
- •2.1.4. Основное уравнение гидростатики. Закон Паскаля
- •2.1.5. Поверхности уровня
- •2.2. Дифференциальные уравнения гидростатики
- •2.2.2. Основное дифференциальное уравнение гидростатики
- •2.2.3. Дифференциальное уравнение поверхности
- •2.3. Основные задачи гидростатики
- •2.4. Основное уравнение гидростатики из уравнений Эйлера. Закон распределения давления
- •2.4.1. Геометрическая интерпретация основного уравнения гидростатики
- •2.4.2. Энергетическая интерпретация основного уравнения гидростатики
- •2.5. Применение закона Паскаля в технике
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины.
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины. Гидравлический пресс. Мультипликатор
- •2.6. Сила давления на плоскую стенку. Гидравлический парадокс
- •2.7. Центр давления
- •2.8. Сила давления жидкости на криволинейные стенки
- •2.9. Закон Архимеда
- •2.10. Относительное равновесие жидкости
- •2.10.1. Движение сосуда с жидкостью прямолинейно в произвольном направлении с постоянным ускорением
- •2.10.2. Движение сосуда с жидкостью вертикально вниз с постоянным ускорением
- •2.10.3. Равномерное вращение цилиндрического сосуда с жидкостью вокруг вертикальной оси
- •2.10.4. Равновесие жидкости в поле центробежных сил при нулевой или слабой гравитация
- •2.11. Формы поверхностей раздела между жидкостью и газом (паром) в условиях динамической невесомости
- •3. Гидродинамика
- •3.2. Виды движения жидкости
- •3.3. Линия тока и траектория частицы, элементарная струйка
- •3.4. Закон сохранения массы. Расход. Уравнение неразрывности
- •3.5. Живое сечение. Смоченный периметр. Гидравлический радиус
- •3.6. Уравнение количества движения для потока жидкости
- •3.7. Дифференциальные уравнения движения идеальной жидкости в форме уравнений Эйлера
- •3.8. Основное дифференциальное уравнение установившегося движения идеальной жидкости
- •3.9. Уравнение Бернулли для струйки идеальной несжимаемой жидкости
- •3.9.1. Геометрический смысл уравнения Бернулли.
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.9.1. Геометрический смысл уравнения Бернулли. Трубка Пито
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.10. Уравнение Бернулли для элементарной струйки вязкой жидкости
- •3.11. Уравнение Бернулли для потока вязкой несжимаемой жидкости
- •3.12. Классификация гидравлических потерь. Гидравлический и пьезометрический уклоны
- •3.13. Применение уравнения Бернулли в технике
- •3.14. Основы гидродинамического подобия
- •3.15. Режимы течения жидкости
- •3.16. Критерий Рейнольдса и гидравлический радиус
- •4. Ламинарное течение жидкости
- •4.2. Расход при ламинарном режиме в круглой трубе. Формула Пуазейля. Коэффициент Кориолиса
- •4.3. Потери на трение. Формула Дарси-Вейсбаха
- •4.4. Влияние теплообмена на профиль скоростей и потери по длине
- •4.5. Начальный участок ламинарного потока
- •4.6. Потери на трение при ламинарном течении в каналах некруглой формы
- •4.7. Ламинарное течение в зазорах
- •4.7.1. Течение через зазор между параллельными стенками под действием умеренного перепада давлений
- •4.7.2. Течение через зазор при больших перепадах давления
- •5. Турбулентное движение жидкости
- •5.1. Пульсация местной скорости в турбулентном потоке
- •5.2. Распределение осреднённых местных скоростей в турбулентном потоке
- •5.3. Гидравлически гладкие и шероховатые трубы
- •5.4. Потери по длине в гидравлически гладких трубах
- •5.6. Влияние шероховатости на потери. График Никурадзе
- •Заключение
- •Библиографический список
- •Оглавление
3.9. Уравнение Бернулли для струйки идеальной несжимаемой жидкости

3.9.1. Геометрический смысл уравнения Бернулли.
Трубка Пито
3.9.2. Энергетический смысл уравнения Бернулли

Рассмотрим частный случай установившегося движения жидкости, когда на неё действует лишь одна массовая сила – сила тяжести. Проекции единичных массовых сил на оси координат будут равны:
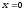 ,
, 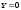 ,
,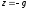 .
.
Подставив эти значения в уравнение (3.16), после преобразования получим
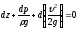 .
.
Проведём
интегрирование этого уравнения, наложив
на него третье ограничение - будем
считать, что жидкость несжимаема, т.е.
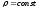 .
.
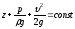 , (3.17)
, (3.17)
или,
подставив
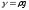 ,
,
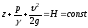 , (3.18)
, (3.18)
где
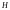 - гидродинамический напор.
- гидродинамический напор.
Уравнение в формах (3.17) и (3.18) обычно называют уравнением Бернулли, отдавая дань заслугам Даниила Бернулли, который первым установил эту закономерность и обосновал её в капитальном труде «Гидродинамика». Как известно, эту монографию, вышедшую в 1738 году, он посвятил Петербургской Академии наук.
Это уравнение показывает, что приращение трёх членов при перемещении частицы жидкости вдоль линии тока равно нулю, т.е. есть величина постоянная.
При установившемся течении траектория жидкой частицы совпадает с линией тока. Поэтому полученное уравнение справедливо для частицы идеальной жидкости, движущейся вдоль линии тока. Учитывая малость сечения струйки, можно считать его справедливым и для элементарной струйки, осевая линия которой совпадает с линией тока.
3.9.1. Геометрический смысл уравнения Бернулли. Трубка Пито
В гидравлике уравнение Бернулли чаще всего используется в форме (3.18)
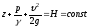 .
.
Все
члены этого уравнения имеют линейную
размерность - [м, см]. Подобно тому, как
первый член этого уравнения представляет
собой некоторую высоту можно и остальные
слагаемые представить как высоты. Не
следует думать, что речь идёт о каких-то
воображаемых высотах. Все эти высоты
можно воспроизвести реально. Выделим
элементарную струйку, возвышающуюся
над горизонтальной плоскостью
 (рис. 3.10).
(рис. 3.10).
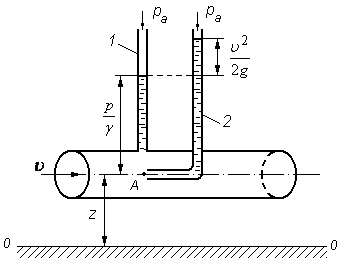
Рис. 3.10. Геометрическая интерпретация уравнения Бернулли
(схема трубки полного давления - Пито)
Каждая из этих высот получила определённое название:
 -
геометрическая или нивелирная высота,
т.е. высота центра тяжести поперечного
сечения струйки, измеренная относительно
некоторой произвольной плоскости
сравнения
-
геометрическая или нивелирная высота,
т.е. высота центра тяжести поперечного
сечения струйки, измеренная относительно
некоторой произвольной плоскости
сравнения
 ;
;
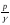 -
пьезометрическая высота, т.е. высота
столба жидкости в трубке пьезометра 1;
-
пьезометрическая высота, т.е. высота
столба жидкости в трубке пьезометра 1;
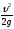 -
высота скоростного напора, т.е.
дополнительная высота, на которую
жидкость поднялась бы в пьезометре при
полном торможении потока в данной точке
А;
-
высота скоростного напора, т.е.
дополнительная высота, на которую
жидкость поднялась бы в пьезометре при
полном торможении потока в данной точке
А;
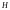 -
высота полного гидродинамического
напора, т.е. сумма указанных трёх высот.
-
высота полного гидродинамического
напора, т.е. сумма указанных трёх высот.
Высота столба жидкости в пьезометре, измеренная относительно точки А, равна пьезометрической высоте в этой точке потока.
Во
второй же трубке жидкость поднимется
на
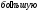 высоту, поскольку скорость в точкеА
упала до нуля и удельная кинетическая
энергия полностью перешла в энергию
давления.
высоту, поскольку скорость в точкеА
упала до нуля и удельная кинетическая
энергия полностью перешла в энергию
давления.
Разность
высот в этих двух трубках, таким образом,
равна удельной кинетической энергии,
или то же самое, высоте скоростного
напора
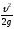 .
.
Полный
гидродинамический напор
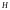 равен сумме трёх указанных высот.
равен сумме трёх указанных высот.
Закон, выражаемый уравнением Бернулли, может быть наглядно представлен для элементарной струйки в виде диаграммы (рис. 3.11).
Отнесём
струйку к системе координат
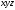 и напишем уравнение Бернулли для трёх
произвольных сечений струйки
и напишем уравнение Бернулли для трёх
произвольных сечений струйки
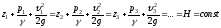 .
.
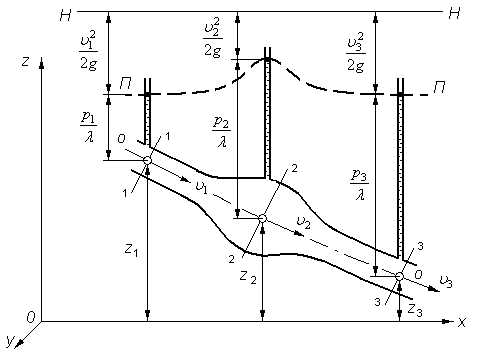
Рис. 3.11. Линии полных напоров Н-Н и пьезометрических
высот П-П вдоль струйки идеальной жидкости
Выбрав
произвольно горизонтальную плоскость
сравнения
 отложим от неё геометрическую высоту
отложим от неё геометрическую высоту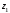 поперечного сечения 1-1 струйки. Затем
надстроим в том же масштабе последовательно
пьезометрическую высоту
поперечного сечения 1-1 струйки. Затем
надстроим в том же масштабе последовательно
пьезометрическую высоту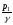 и высоту скоростного напора
и высоту скоростного напора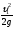 .
Сумма этих высот равна высоте
.
Сумма этих высот равна высоте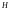 полного гидродинамического напора,
которая по всей длине струйки идеальной
жидкости остаётся одинаковой. На высоте
полного гидродинамического напора,
которая по всей длине струйки идеальной
жидкости остаётся одинаковой. На высоте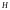 расположена горизонтальная линия
расположена горизонтальная линия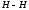 ,
которую принято называть линией полного
гидродинамического напора или сокращённо
напорной линией.
,
которую принято называть линией полного
гидродинамического напора или сокращённо
напорной линией.
Теперь
в любом другом произвольном сечении
струйки (например, в сечении 2-2) можно
не зная даже величины давления в этом
сечении, построить все три высоты,
входящие в уравнение Бернулли. Удобнее
всего построение начать с высоты
скоростного напора, величина которой
может быть легко найдена из геометрии
струйки с помощью уравнения расхода
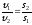 ,
,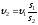 .
Полученную таким образом высоту
.
Полученную таким образом высоту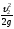 отложим вниз от плоскости полного
напора. Дополнительный вертикальный
отрезок до центра тяжести сечения
струйки и будет представлять искомую
пьезометрическую высоту
отложим вниз от плоскости полного
напора. Дополнительный вертикальный
отрезок до центра тяжести сечения
струйки и будет представлять искомую
пьезометрическую высоту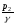 ,
а вертикальный отрезок до центра тяжести
сечения до плоскости сравнения
,
а вертикальный отрезок до центра тяжести
сечения до плоскости сравнения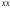 - геометрическую высоту
- геометрическую высоту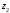 .
.
Соединяя плавными кривыми вершины всех трёх высот, получаем характерные элементы «диаграммы Бернулли»:
-
линию геометрических высот (осевую
линию
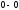 струйки);
струйки);
-
пьезометрическую линию
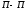 (геометрическое место вершин
пьезометрических высот);
(геометрическое место вершин
пьезометрических высот);
-
напорную линию
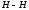 (геометрическое место вершин высот
полного гидродинамического напора).
(геометрическое место вершин высот
полного гидродинамического напора).
Итак, рисунок 3.11 даёт геометрическое истолкование уравнения Бернулли:
1) При установившемся движении идеальной жидкости сумма трёх высот есть величина постоянная, и называется полным напором;
2)
Если сечение расширяется и, следовательно,
скорость уменьшается, то уменьшается
скоростной напор, но возрастает сумма
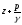 .
.
Закономерности, найденные для струйки, справедливы и для одномерных потоков конечного сечения.
