3.9.2. Энергетический смысл уравнения Бернулли

Если рассматривать уравнение Бернулли как уравнение энергии, то каждое из слагаемых должно измеряться в единицах работы. Чтобы перевести уравнение (3.18) в уравнение работы надо умножить его на единицу силу, например, на 1Н, тогда размерность каждого слагаемого будет выражена в Нм (Дж).

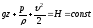
Условимся называть удельной энергией жидкости энергию, отнесённую к единице массы. Тогда:

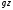- удельная потенциальная энергия положения, т.к. частица жидкости массой , находясь на высоте, обладает энергией положения;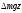

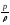- удельная потенциальная энергия давления движущейся жидкости, т.к. частица жидкости массой при давленииобладает способностью подняться на высоту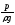и приобрести потенциальную энергию;

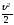- удельная кинетическая энергия давления движущейся жидкости, т.к. частица жидкости массой обладает кинетической энергией.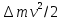

Итак, энергетический смысл уравнения Бернулли:

1) При установившемся движении идеальной жидкости полная удельная энергия в любом поперечном сечении равна сумме трёх удельных энергий - положения, давления и кинетической и есть величина постоянная;

2) При переходе от одного сечения струйки к любому другому её поперечному сечению удельная энергия одного вида может изменяться только за счёт изменения удельных энергий других видов.

Иными словами, уравнение Бернулли представляет собой частное выражение закона сохранения энергии применительно к струйке идеальной жидкости.

3.10. Уравнение Бернулли для элементарной струйки вязкой жидкости

Вязкая жидкость при движении испытывает сопротивление, поэтому её удельная энергия не может сохраняться неизменной вдоль струйки. На преодоление трения расходуется часть энергии, которая превращается в тепловую энергию, невозвратимую для рассматриваемой движущейся жидкости. Происходит так называемая диссипация (рассеяние) энергии в пространстве. Кроме того, энергия теряется на преодоление других различных видов сопротивлений.

В соответствии с этим при движении вязкой жидкости в уравнении Бернулли надо ввести поправку на потери напора по длине струйки. Выделим в потоке элементарную струйку (рис. 3.12).

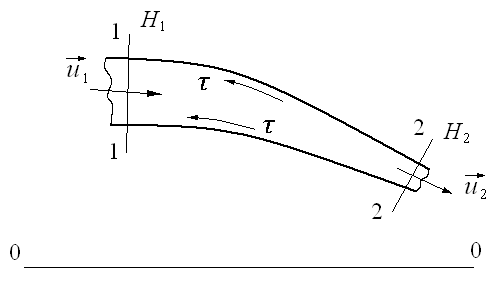
Рис. 3.12. Элементарная струйка

Обозначим полную удельную энергию в сечении 1-1 через 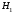, в сечении 2-2 через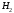, а потери напора -.

Для идеальной струйки

,

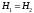А для реальной струйки в силу необратимых потерь на трение

.

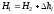В результате получим следующую запись уравнения Бернулли для элементарной струйки вязкой жидкости

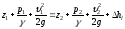. (3.19)

Полученное уравнение Бернулли справедливо для элементарной струйки вязкой жидкости.

3.11. Уравнение Бернулли для потока вязкой несжимаемой жидкости

Разобьём установившийся параллельноструйный поток на элементарные струйки и, выделив одну из них, определим её мощность в поперечноном сечении 1-1 потока (рис. 3.12).

При этом под мощностью будем понимать энергию жидкости, протекающей через поперечное сечение струйки в единицу времени. Учитывая, что энергия струйки на единицу веса жидкости, равна высоте полного гидродинамического напора и что в единицу времени через поперечное сечение протекает жидкость, вес которой равен весовому расходу струйки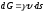, можно записать, что

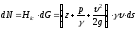. (3.20)

А теперь, интегрируя мощность по всей площади живого сечения, получим мощность потока в данном живом сечении:

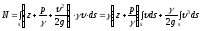. (3.21)

Первый из интегралов равен объёмному расходу потока, выраженному через среднюю скорость:

. (3.22)

Что касается второго интеграла, то ясно, что

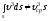. (3.23)

Однако это неравенство можно превратить в равенство, вводя поправочный коэффициент

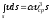, (3.24).

Подставив (3.22) и (3.24) в уравнение (3.21), получим

.

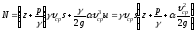Отнеся мощность потока к весу жидкости 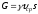, получим высоту полного гидродинамического напора в данном живом сечении потока:

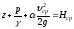. (3.25)

Третье слагаемое в выражении (3.25) представляет собой удельную кинетическую энергию (высоту скоростного напора) в данном живом сечении потока.

Из выражения (3.24) следует, что 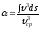- коэффициент, учитывающий неравномерность распределения местных скоростей по сечению потока.

При равномерном распределении скоростей по сечению, т.е. при 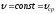коэффициент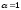. Чем более равномерно распределены скорости, тем меньше отличается коэффициент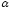от единицы.

При равномерном движении жидкости коэффициент приблизительно равен

.

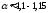При неравномерном движении значения 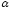могут иногда значительно отличаться от единицы. Вместе с тем при выполнении гидравлических расчётов коэффициент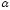часто принимают равным единице, т.е. вовсе не учитывают.

Выражение (3.25) даёт величину полного гидродинамического напора в одном живом сечении потока. Чтобы получить уравнение Бернулли для потока, необходимо сравнить значения полного напора в разных сечениях.

Обозначим средние значения полного напора в сечениях 1-1 и 2-2 через 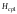и. Тогда,

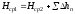, (3.26)

где 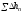- суммарные потери полного напора на участке между рассматриваемыми сечениями.

Запишем уравнение (3.26) применительно к двум сечениям в развёрнутой форме

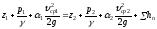. (3.27)

Это и есть уравнение Бернулли для установившегося потока вязкой несжимаемой жидкости.

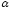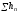От уравнения (3.19) для элементарной струйки идеальной жидкости оно отличается коэффициентом , учитывающим неравномерность распределения скоростей, и членом, представляющим собой потерю полного напора, а скорости, входящие в это уравнение, являются средними скоростями.

Как и уравнение Бернулли в формах (3.17) и (3.18) уравнения (3.19) и (3.27) справедливы лишь при отсутствии инерционных сил переносного движении системы (например, для потока в неподвижном или равномерно и прямолинейно перемещающемся трубопроводе).