
3. Расчет цепей постоянного тока
3.1. Модель цепи постоянного тока
Если в электрической цепи действуют постоянные напряжения и протекают постоянные токи, то модели реактивных элементов LиCсущественно упрощаются.
Модель сопротивления
![]() остается прежней и связь между напряжением
остается прежней и связь между напряжением![]() и током
и током![]() определяется законом Ома в виде
определяется законом Ома в виде
![]() .
(3.1)
.
(3.1)
В идеальной индуктивности мгновенные значения напряжения и тока связаны соотношением
![]() .
(3.2)
.
(3.2)

Аналогично в емкости связь между мгновенными значениями напряжения и тока определяется в виде
![]() .
(3.3)
.
(3.3)

53
Таким образом, в модели цепи постоянного тока присутствуют только сопротивления (модели резисторов) и источники сигнала, а реактивные элементы (индуктивности и емкости) отсутствуют.
3.2. Расчет цепи на основе закона Ома
Этот метод удобен для расчета сравнительно
простых цепей с одним источником
сигнала. Он предполагает вычисление
сопротивлений участков цепи, для которых
известна величина тока (или напряжения),
с последующим определением неизвестного
напряжения (или тока). Рассмотрим пример
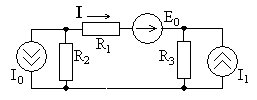
расчета цепи, схема которой приведена
на рис. 3.1, при токе идеального источника![]() А
и сопротивлениях
А
и сопротивлениях![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом.
Необходимо определить токи ветвей
Ом.
Необходимо определить токи ветвей![]() и
и![]() ,
а также напряжения на сопротивлениях
,
а также напряжения на сопротивлениях![]() ,
,![]() и
и![]() .
.
 Известен
ток источника
Известен
ток источника![]() ,
тогда можно вычислить сопротивление
цепи
,
тогда можно вычислить сопротивление
цепи![]() относительно зажимов источника тока
(параллельного соединения сопротивления
относительно зажимов источника тока
(параллельного соединения сопротивления![]() и последовательно соединен-
и последовательно соединен-
Рис. 3.1. ных
сопротивлений
![]() и
и![]() ),
),
![]() .
.
Тогда напряжение
![]() на источнике тока (на сопротивлении
на источнике тока (на сопротивлении![]() )
равно
)
равно
![]() В.
В.
54
Затем можно найти токи ветвей
![]() А,
А,
![]() А.
А.
Полученные результаты можно проверить
с помощью первого закона Кирхгофа в
виде
![]() .
Подставляя вычисленные значения, получим
.
Подставляя вычисленные значения, получим![]() А,
что совпадает с величиной тока источника.
А,
что совпадает с величиной тока источника.
Зная токи ветвей, нетрудно найти
напряжения на сопротивлениях (величина
![]() уже найдена)
уже найдена)
![]() В,
В,
![]() В.
В.
По второму закону Кирхгофа
![]() .
Складывая полученные результаты,
убеждаемся в его выполнении.
.
Складывая полученные результаты,
убеждаемся в его выполнении.
3.3. Общий метод расчета цепи на основе законов Ома
и Кирхгофа
Общий метод расчета токов и напряжений в электрической цепи на основе законов Ома и Кирхгофа пригоден для расчета сложных цепей с несколькими источниками сигнала.
Расчет начинается с задания обозначений и положительных направлений токов и напряжений для каждого элемента (сопротивления) цепи.
Система уравнений включает в себя подсистему компонентных уравнений, связывающих по закону Ома токи и напряжения в каждом элементе (сопротивлении) и подсистему
55
топологических уравнений, построенную на основе первого и второго законов Кирхгофа.
Рассмотрим расчет простой цепи из предыдущего примера, показанной на рис. 3.1, при тех же исходных данных.
Подсистема компонентных уравнений имеет вид
 (3.4)
(3.4)
В цепи имеется два узла (![]() )
и две ветви, не содержащие идеальных
источников тока (
)
и две ветви, не содержащие идеальных
источников тока (![]() ).
Следовательно, необходимо записать
одно уравнение (
).
Следовательно, необходимо записать
одно уравнение (![]() )
по первому закону Кирхгофа,
)
по первому закону Кирхгофа,
![]() ,
(3.5)
,
(3.5)
и одно уравнение второго закона Кирхгофа
(![]() ),
),
![]() ,
(3.6)
,
(3.6)
которые и образуют подсистему топологических уравнений.
Уравнения (3.4)-(3.6) являются полной системой уравнений цепи. Подставляя (3.4) в (3.6), получим
![]() ,
(3.7)
,
(3.7)
а, объединив (3.5) и (3.7), получим два уравнения с двумя неизвестными токами ветвей,
 (3.8)
(3.8)
56
Выражая из первого уравнения (3.8) ток
![]() и подставляя его во второе, найдем
значение тока
и подставляя его во второе, найдем
значение тока![]() ,
,
![]() А,
(3.9)
А,
(3.9)
а затем найдем
![]() А.
По вычисленным токам ветвей из компонентных
уравнений (3.4) определим напряжения.
Результаты расчета совпадают с полученными
ранее в подразделе 3.2.
А.
По вычисленным токам ветвей из компонентных
уравнений (3.4) определим напряжения.
Результаты расчета совпадают с полученными
ранее в подразделе 3.2.
Рассмотрим более сложный пример расчета
цепи в схеме, показанной на рис. 3.2, с
параметрами
![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,![]() Ом,
Ом,
![]()
 В,
В,![]() А.
А.
Цепь содержит
![]() узла (их номера указаны в кружках) и
узла (их номера указаны в кружках) и![]() ветвей, не содержащих идеальные источники
тока. Система компонентных уравнений
цепи имеет вид
ветвей, не содержащих идеальные источники
тока. Система компонентных уравнений
цепи имеет вид
Рис. 3.2

 (3.10)
(3.10)
По первому закону Кирхгофа необходимо
записать
![]() уравнения (узел 0 не используется),
уравнения (узел 0 не используется),
57
 (3.11)
(3.11)
По второму закону Кирхгофа составляется
![]() уравнения для трех независимых контуров,
отмеченных на схеме окружностями со
стрелками (внутри указаны номера
контуров),
уравнения для трех независимых контуров,
отмеченных на схеме окружностями со
стрелками (внутри указаны номера
контуров),
 (3.12)
(3.12)
Подставляя (3.11) в (3.13), совместно с (3.12)
получим систему шести
![]() уравнений вида
уравнений вида
 (3.13)
(3.13)

Из второго и третьего уравнений выразим
 (3.14)
(3.14)
а из первого
![]() ,
тогда подставив
,
тогда подставив![]() и
и![]() ,
получим
,
получим![]() .
Подставляя токи
.
Подставляя токи![]() ,
,![]() и
и![]() в уравнения второго закона Кирхгофа,
запишем систему из трех уравнений
в уравнения второго закона Кирхгофа,
запишем систему из трех уравнений
58

которую после приведения подобных запишем в виде
 (3.15)
(3.15)
Обозначим
 ,
(3.16)
,
(3.16)
и из третьего уравнения системы (3.15) запишем
![]() .
(3.17)
.
(3.17)
Подставляя полученное значение
![]() в первые два уравнения (3.15), получим
систему из двух уравнений вида
в первые два уравнения (3.15), получим
систему из двух уравнений вида
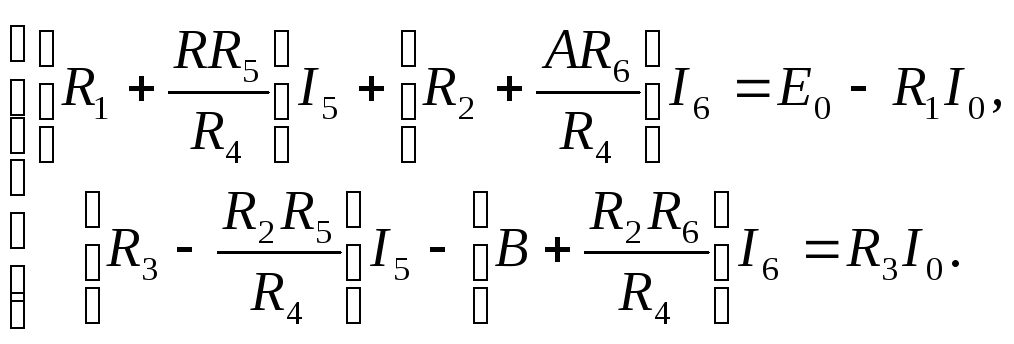 (3.18)
(3.18)
Из второго уравнения (3.18) получим
59
![]() ,
(3.19)
,
(3.19)
тогда из первого уравнения найдем ток
![]()
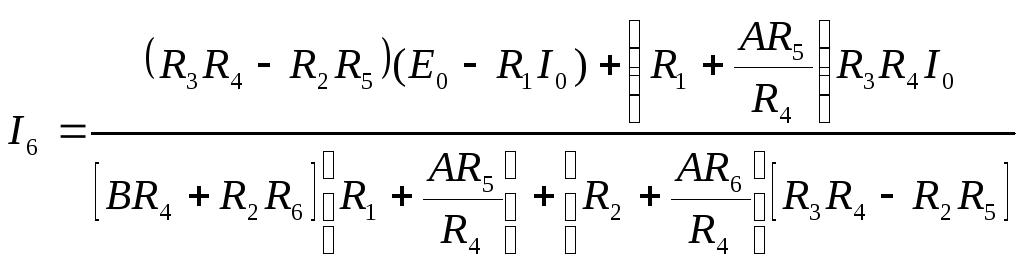 .
(3.20)
.
(3.20)
Вычислив
![]() ,
из (3.19) найдем
,
из (3.19) найдем![]() ,
из (3.17) вычислим
,
из (3.17) вычислим![]() ,
а затем из уравнений подстановки найдем
токи
,
а затем из уравнений подстановки найдем
токи![]() ,
,![]() ,
,![]() .
.
Как видно, аналитические вычисления достаточно громоздки, и для численных расчетов целесообразней использовать современные программные пакеты, например, MathCAD2001. Пример программы показан на рис. 3.3.
Матрица - столбец
![]() содержит значения токов
содержит значения токов![]() А,
А,![]() А,
А,![]() А.
Остальные
А.
Остальные
токи вычисляются согласно уравнениям (3.14) и равны
![]() А,
А,![]() А,
А,![]() А.
Вычисленные значения токов совпадают
с полученными по приведенным выше
формулам.
А.
Вычисленные значения токов совпадают
с полученными по приведенным выше
формулам.
Общий метод расчета цепи по уравнениям
Кирхгофа приводит к необходимости
решения
![]() линейных алгебраических уравнений. При
большом числе ветвей
линейных алгебраических уравнений. При
большом числе ветвей![]() возникают математические и вычислительные
трудности. Это означает, что целесообразно
искатьметоды расчета, требующие
составления и решения меньшего числа
уравнений.
возникают математические и вычислительные
трудности. Это означает, что целесообразно
искатьметоды расчета, требующие
составления и решения меньшего числа
уравнений.
60

Рис. 3.3
3.4. Метод контурных токов
Метод контурных токов базируется
на уравненияхвторого закона
Кирхгофаи приводит к необходимости
решения![]() уравнений,
уравнений,![]() -
число всех ветвей, в том числе и содержащих
идеальные источники тока.
-
число всех ветвей, в том числе и содержащих
идеальные источники тока.
В цепи выбираются
![]() независимых контуров и для каждого
независимых контуров и для каждого![]() -го
из них вводится кольцевой (замкнутый)
контурный ток
-го
из них вводится кольцевой (замкнутый)
контурный ток![]() (двойная индексация позволяет отличать
кон-
(двойная индексация позволяет отличать
кон-
61
турные токи от токов ветвей). Через
контурные токи можно выразить все токи
ветвей и для каждого независимого
контура записать уравнения второго
закона Кирхгофа. Система уравнений
содержит
![]() уравнений, из которых определяются все
контурные токи. По найденным контурным
токам находятся токи или напряжения
ветвей (элементов).
уравнений, из которых определяются все
контурные токи. По найденным контурным
токам находятся токи или напряжения
ветвей (элементов).
 Рассмотрим
пример цепи на рис. 3.1. На рис 3.4 приведена
схема с указанием обозначений и
положительных направлений двух контурных
токов
Рассмотрим
пример цепи на рис. 3.1. На рис 3.4 приведена
схема с указанием обозначений и
положительных направлений двух контурных
токов![]() и
и![]() (
(![]() ,
,![]() ,
,![]() ).
).
Рис. 3.4 Через
ветвь
![]() проте-
проте-
кает только
контурный ток
![]() и его направление совпадает с
и его направление совпадает с![]() ,
поэтому ток ветви
,
поэтому ток ветви![]() равен
равен
![]() .
(3.21)
.
(3.21)
В ветви
![]() протекают два контурных тока, ток
протекают два контурных тока, ток![]() совпадает по направлению с
совпадает по направлению с![]() ,
а ток
,
а ток![]() имеет противоположное направление,
следовательно
имеет противоположное направление,
следовательно
![]() .
(3.22)
.
(3.22)
Для контуров, не содержащих идеальные источники тока, составляем уравнения второго закона Кирхгофа с использованием закона Ома, в данном примере записывается одно уравнение
![]() .
(3.23)
.
(3.23)
Если в контур включен идеальный источник тока, то для него
62
уравнение второго закона Кирхгофа не составляется, а его контурный ток равен току источника с учетом их положительных направлений, в рассматриваемом случае
![]() .
(3.24)
.
(3.24)
Тогда система уравнений принимает вид
 .
(3.25)
.
(3.25)
В результате подстановки второго уравнения в первое получим
![]() ,
(3.26)
,
(3.26)
тогда ток
![]() равен
равен
![]() А,
(3.27)
А,
(3.27)
а ток
![]() А.
Из (3.21)
А.
Из (3.21)![]() А,
а из (3.22) соответственно
А,
а из (3.22) соответственно![]() А,
что полностью совпадает с полученными
ранее результатами. При необходимости
по найденным значениям токов ветвей по
закону Ома можно вычислить напряжения
на элементах цепи.
А,
что полностью совпадает с полученными
ранее результатами. При необходимости
по найденным значениям токов ветвей по
закону Ома можно вычислить напряжения
на элементах цепи.
Рассмотрим более сложный пример цепи
на рис. 3.2, схема которой с заданными
контурными токами показана на рис. 3.5.
В этом случае число ветвей
![]() ,
количество узлов
,
количество узлов![]() ,
тогда число независимых контуров и
уравнений по методу контурных токов
равно
,
тогда число независимых контуров и
уравнений по методу контурных токов
равно![]() .
Для токов ветвей можно записать
.
Для токов ветвей можно записать
63
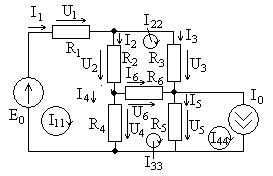
Рис. 3.5
 (3.28)
(3.28)

Первые три контура не содержат идеальных источников тока, тогда с учетом (3.28) и использованием закона Ома для них можно записать уравнения второго закона Кирхгофа,
 (3.29)
(3.29)
В четвертом контуре присутствует идеальный источник тока, поэтому для него уравнение второго закона Кирхгофа не составляется, а контурный ток равен току источника (они совпадают по направлению),
![]() .
(3.30)
.
(3.30)
Подставляя (3.30) в систему (3.29), после преобразования получим три уравнения для контурных токов в виде
64
 (3.31)
(3.31)
Систему уравнений (3.31) можно решить аналитически (например, методом подстановки – проделайте это), получив формулы для контурных токов, а затем из (3.28) определить токи ветвей. Для численных расчетов удобно использовать пакет программMathCAD, пример программы показан на рис. 3.6. Результаты вычислений совпадают с расчетами, приведенными на рис. 3.3. Как видно, метод контурных токов требует составления и решения меньшего числа уравнений по сравнению с общим методом расчета по уравнениям Кирхгофа.

Рис. 3.6
65
3.5. Метод узловых напряжений
Метод узловых напряженийбазируется
на первом законе Кирхгофа, при этом
число уравнений равно![]() .
.
В цепи выделяются все
![]() узлов и один из них выбирается в качествебазисного, которому присваивается
нулевой потенциал. Потенциалы (напряжения)
узлов и один из них выбирается в качествебазисного, которому присваивается
нулевой потенциал. Потенциалы (напряжения)![]() …
…![]() остальных
остальных![]() узлов отсчитываются от базисного, их
положительные направления обычно
выбираются стрелкой в базисный узел.
Через узловые напряжения с использованием
закона Ома и второго закона Кирхгофа
выражаются токи всех ветвей
узлов отсчитываются от базисного, их
положительные направления обычно
выбираются стрелкой в базисный узел.
Через узловые напряжения с использованием
закона Ома и второго закона Кирхгофа
выражаются токи всех ветвей
и для
![]() узлов записываются уравнения первого
закона Кирхгофа.
узлов записываются уравнения первого
закона Кирхгофа.
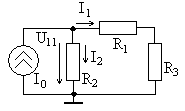 Рассмотрим
пример цепи, показанной на рис. 3.1, для
метода узловых напряжений ее схема
показана на рис. 3.7. Нижний узел обозначен
как базисный (для этого используется
символ «земля» - точка нулевого
потенциала), напряжение верхнего узла
относительно базисного обо-
Рассмотрим
пример цепи, показанной на рис. 3.1, для
метода узловых напряжений ее схема
показана на рис. 3.7. Нижний узел обозначен
как базисный (для этого используется
символ «земля» - точка нулевого
потенциала), напряжение верхнего узла
относительно базисного обо-
Рис. 3.7 значено как
![]() .
Выразим через
.
Выразим через
него токи ветвей
 (3.32)
(3.32)
По первому закону Кирхгофа с учетом
(3.32) запишем единственное уравнение
метода узловых напряжений (![]() ),
),
66
![]() .
(3.33)
.
(3.33)
Решая уравнение, получим
![]() ,
(3.34)
,
(3.34)
а из (3.32) определим токи ветвей
 (3.35)
(3.35)
Полученные результаты совпадают с полученными рассмотренными ранее методами.
 Рассмотрим
более сложный пример цепи, показанной
на рис. 3.2 при тех же исходных данных, ее
схема показана на рис. 3.8. В цепи
Рассмотрим
более сложный пример цепи, показанной
на рис. 3.2 при тех же исходных данных, ее
схема показана на рис. 3.8. В цепи![]() узла, нижний выбран базисным, а три
остальные обозначены номерами в кружках.
Введены
узла, нижний выбран базисным, а три
остальные обозначены номерами в кружках.
Введены
положительные на- Рис. 3.8
правления и обозна-
чения узловых напряжений
![]() ,
,![]() и
и![]() .
.
По Закону Ома с использованием второго закона Кирхгофа определим токи ветвей,
67

 (3.36)
(3.36)
По первому закону Кирхгофа для узлов с номерами 1, 2 и 3 необходимо составить три уравнения,
 (3.37)
(3.37)
Подставляя (3.36) в (3.37), получим систему уравнений метода узловых напряжений,
 (3.38)
(3.38)
После преобразования и приведения подобных получим
 (3.39)
(3.39)
68
Программа расчета узловых напряжений и токов ветвей приведена на рис. 3.9. Как видно, полученные результаты совпадают с полученными ранее другими методами расчета.
Проведите аналитический расчет узловых напряжений, получите формулы для токов ветвей и вычислите их значения.

Рис. 3.9
69
3.6. Метод наложения
Метод наложениязаключается в следующем.

Расчет проводится следующим образом.
В цепи, содержащей несколько источников,
поочередно выбирается каждый из них, а
остальные отключаются. При этом образуются
цепи с одним источником, число которых
равно количеству источников в исходной
цепи. В каждой из них проводится расчет
искомого сигнала, а результирующий
сигнал определяется их суммой. В качестве
примера рассмотрим расчет тока
![]() в цепи, показанной на рис. 3.2, ее схема
показана на рис. 3.10а.
в цепи, показанной на рис. 3.2, ее схема
показана на рис. 3.10а.

Рис. 3.10
70
При выключении идеального источника
тока (его цепь разрывается) получается
цепь, показанная на рис. 3.9б, в которой
любым из рассмотренных методов
определяется ток
![]() .
Затем выключается идеальный источник
напряжения (он заменяется коротким
замыканием) и получается цепь, показанная
.
Затем выключается идеальный источник
напряжения (он заменяется коротким
замыканием) и получается цепь, показанная
на рис. 3.9а, в которой находится ток
![]() .
Искомый ток
.
Искомый ток![]() равен
равен
![]() .
.
Проведите аналитические и численные расчеты самостоятельно, сравните с полученными ранее результатами, например, (3.20).
3.7. Сравнительный анализ методов расчета
Метод расчета, основанный на законе Ома, пригоден для сравнительно простых цепей с одним источником. Его нельзя использовать для анализа цепей сложной структуры, например, мостового типа вида рис.3.9.
Общий метод расчета цепи на основе
уравнений законов Ома и Кирхгофа
универсален, но требует составления и
решения системы из
![]() уравнений, которая легко преобразуется
в систему из
уравнений, которая легко преобразуется
в систему из![]() уравнений. При большом числе ветвей
резко возрастают вычислительные затраты,
особенно при необходимости аналитических
расчетов.
уравнений. При большом числе ветвей
резко возрастают вычислительные затраты,
особенно при необходимости аналитических
расчетов.
Методы контурных токов и узловых
напряжений более эффективны, так как
приводят к системам с меньшим числом
уравнений, равным соответственно
![]() и
и![]() .
При условии
.
При условии
![]() или
или![]() (3.40)
(3.40)
метод контурных токов эффективнее, а иначе целесообразно применять метод узловых напряжений.
71
Метод наложения удобен, когда при отключении источников происходит резкое упрощение цепи.
В системах схемотехнического моделирования цепей, например, MicroCAPилиOrCADв основном применяют метод узловых напряжений.
3.8. Задания для самостоятельного решения
Задание 3.1 С помощью
закона Ома определите напряжение![]() в цепях, схемы которых показаны на рис.
3.11 при
в цепях, схемы которых показаны на рис.
3.11 при![]() В,
В,![]() мА,
мА,![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм.
кОм.

Рис. 3.11
Задание 3.2Общим методом расчета
на основе законов Ома и Кирхгофа
определите ток![]() в цепях, схемы которых показаны на рис.
3.11 при
в цепях, схемы которых показаны на рис.
3.11 при![]() В,
В,![]() В,
В,![]() мА,
мА,![]() мА,
мА,![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм.
кОм.
Задание 3.3Методами контурных токов,
узловых напряжений и наложения определите
ток![]() в цепях, схемы которых показаны на рис.
3.12, параметры цепи возьмите из задания
3.1, сравните полученные результаты.
в цепях, схемы которых показаны на рис.
3.12, параметры цепи возьмите из задания
3.1, сравните полученные результаты.
72

Рис. 3.12
 Задание
3.4.Методами контурных токов и узловых
напряжений определите ток
Задание
3.4.Методами контурных токов и узловых
напряжений определите ток![]() в цепи, схема которой показана на рис.
3.13 при
в цепи, схема которой показана на рис.
3.13 при![]() В,
В,![]() мА,
мА,![]() мА,
мА,![]() кОм,
кОм,![]() кОм,
кОм,
![]() кОм.
Рис. 3.13
кОм.
Рис. 3.13

Задание 3.5. Общим методом расчета,
методами контурных токов и узловых
напряжений определите в цепи рис. 3.14
напряжение![]() при
при![]() мА
мА![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм,
кОм,![]() кОм.
Проведите сравнительный анализ
кОм.
Проведите сравнительный анализ
методов расчета. Рис. 3.14
73
4. ГАРМОНИЧЕСКИЕ ТОКИ И НАПРЯЖЕНИЯ
В ЛИНЕЙНЫХ ЦЕПЯХ
4.1. Гармонические ток и напряжение в элементах цепи
В элементах цепи R,L, иCвзаимосвязь произвольных мгновенных значений тока и напряжения определяется законом Ома, необходимые соотношения приведены в табл. 1.1.
 Рассмотримгармоническиеток и напряжение на
элементе Э (рис. 4.1) в виде
Рассмотримгармоническиеток и напряжение на
элементе Э (рис. 4.1) в виде
 (4.1)
(4.1)
Рис. 4.1
Для сопротивления Rможно записать
![]() .
(4.2)
.
(4.2)
Сравнивая полученный результат с выражением для напряжения из (4.1), получим выражение закона Ома для амплитуд тока и напряжения.
![]() ,
(4.3)
,
(4.3)
и соотношение для начальных фаз
![]() .
(4.4)
.
(4.4)
Как видно из (4.3), амплитуды (и действующие значения) гармонических тока и напряжения в сопротивлении связанызаконом Омав классической формулировке прямой пропорциональности.
74
Начальные фазы тока
![]() и напряжения
и напряжения![]() в сопротивленииодинаковы, сдвиг
фаз
в сопротивленииодинаковы, сдвиг
фаз![]() между напряжением и током равен нулю,
между напряжением и током равен нулю,
![]() .
(4.5)
.
(4.5)
Мгновенная мощность (1.6) гармонических сигналов в сопротивлении равна
![]() ,
(4.6)
,
(4.6)
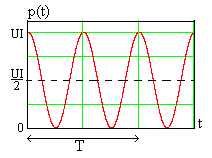
где
![]() .
Ее зависимость от времени показана на
рис. 4.2. Величина
.
Ее зависимость от времени показана на
рис. 4.2. Величина![]() всегда положительна, то есть
сопротивление толькопотребляет
мощностьот источника сигнала. Это
гармоническая функция времени с
периодом по-
всегда положительна, то есть
сопротивление толькопотребляет
мощностьот источника сигнала. Это
гармоническая функция времени с
периодом по-
вторения в два раза меньше пе- Рис. 4.2
риода сигнала.
Средняя мощность (1.8) гармонических сигналов в сопротивлении определяется выражением
![]() ,
(4.7)
,
(4.7)
где
![]() и
и![]() - действующие значения тока и напряжения,
- действующие значения тока и напряжения,
![]() .
(4.8)
.
(4.8)
75
Это значение показано пунктирной линией на временной диаграмме рис. 4.2.
В емкости Cмгновенные значения тока и напряжения связаны соотношением (табл.1.1)
![]() .
(4.9)
.
(4.9)
После преобразования тригонометрической функции к канонической форме гармонического сигнала получим
![]() .
(4.10)
.
(4.10)
Сравнивая (4.10) с формулой тока из (4.1), можно записать
![]() ,
(4.11)
,
(4.11)
![]() .
(4.12)
.
(4.12)
Введем обозначения
![]() ,
(4.13)
,
(4.13)
![]() ,
(4.14)
,
(4.14)
где
![]() -модуль реактивного сопротивления
емкости (Ом), а
-модуль реактивного сопротивления
емкости (Ом), а![]() -реактивная проводимость емкости
(См=1/Ом). Позднее увидим, что реактивное
сопротивление емкостиотрицательно.
-реактивная проводимость емкости
(См=1/Ом). Позднее увидим, что реактивное
сопротивление емкостиотрицательно.
Из (4.11) получим уравнения связи амплитуд (и действующих значений) гармоническихтока и напряжения в емкости
76
![]() ,
(4.15)
,
(4.15)
которые представляют собой выражение закона Омадля емкости в классической формулировке прямой пропорциональности.
Из (4.12) следует, что гармонический ток
в емкости опережает по фазе приложенное
к ней напряжение(напряжение отстает
по фазе от тока) на угол![]() радиан или 900. Сдвиг фаз между
напряжением и током в емкости равен
радиан или 900. Сдвиг фаз между
напряжением и током в емкости равен

![]() .
(4.16)
.
(4.16)
На рис. 4.3 показаны временные диаграммы
тока и напряжения в емкости. Ток
![]() опережает по фазе напряжение на 900,
что отражается навременной
диаграмме смещением
опережает по фазе напряжение на 900,
что отражается навременной
диаграмме смещением
кривой тока влево на чет- Рис. 4.3
верть периода.
Мгновенная мощность в емкости из (4.1) и (4.9) равна
![]() ,
,
а после тригонометрических преобразований получим
![]() .
(4.17)
.
(4.17)
Временная диаграмма мгновенной мощности показана на рис. 4.4
77
 Мгновенная
мощность электрических сигналов в
емкости может быть положительной
(емкость накапливает энергию электрического
поля) и отрицательной (емкость отдает
во внешнюю цепь ранее накопленную
энергию).Средняя мощность гармонических
Мгновенная
мощность электрических сигналов в
емкости может быть положительной
(емкость накапливает энергию электрического
поля) и отрицательной (емкость отдает
во внешнюю цепь ранее накопленную
энергию).Средняя мощность гармонических
сигналов в емкости равна нулю, то
Рис. 4.4 есть емкость не потребляет мощ-
ность от гармонического источника.
Для индуктивности Lмгновенные значения тока и напряжения связаны соотношением закона Ома из табл.1.1, тогда с учетом выражения для тока из (4.1) получим
![]() ,
,
а после преобразований
![]() .
(4.18)
.
(4.18)
Сравнивая (4.18) с выражением для напряжения (4.1), получим уравнения связи для амплитуд (действующих значений) тока и напряжения
![]() (4.19)
(4.19)
и их начальных фаз
![]() .
(4.20)
.
(4.20)
Введем обозначения
78
![]() ,
(4.21)
,
(4.21)
![]() ,
(4.22)
,
(4.22)
где
![]() -реактивное сопротивление индуктивности
(Ом), а
-реактивное сопротивление индуктивности
(Ом), а![]() -модуль реактивной проводимости
индуктивности (См=1/Ом). Позднее увидим,
что реактивная проводимость индуктивностиотрицательна.
-модуль реактивной проводимости
индуктивности (См=1/Ом). Позднее увидим,
что реактивная проводимость индуктивностиотрицательна.
Тогда получим выражения закона Омадля амплитуд (действующих значений) тока и напряжения в индуктивности
![]() .
(4.23)
.
(4.23)
Согласно (4.20) гармонический ток в
индуктивности отстает по фазе от
напряжения(напряжение опережает по
фазе ток) на угол![]() радиан или 900. Сдвиг фаз между
напряжением и током в индуктивности
равен
радиан или 900. Сдвиг фаз между
напряжением и током в индуктивности
равен

![]() .
(4.24)
.
(4.24)
Временные диаграммы тока и напряжения в индуктивности показаны на рис. 4.5. В отличие от аналогичных графиков для емкости на рис. 4.3 ток и напряжение меняются
местами, кривая напряже- Рис. 4.5
ния смещена вправо отно-
сительно тока на четверть периода, что соответствует опережению по фазе на 900.
79
Мгновенная мощность гармонических сигналов в индуктивности равна
![]() ,
(4.25)
,
(4.25)
а после тригонометрических преобразований получим
![]() .
(4.26)
.
(4.26)
Временная диаграмма мгновенной мощности в индуктивности совпадает с показанной на рис. 4.4 для емкости.
Средняя мощность гармонических сигналов в индуктивности (как и в емкости) равна нулю, то есть индуктивность не потребляет мощность от гармонического источника.
В табл. 4.1 приведены сводные результаты для гармонических сигналов в элементах цепи.
Таблица 4.1
|
Элемент |
Ток |
Напряжение |
Средняя мощность |
|
R |
|
|
|
|
C |
|
|
|
|
L |
|
|
|
4.2. Средняя мощность гармонических сигналов в
линейном двухполюснике
Рассмотрим двухполюсник
(ДП) на рис. 4.6, через который протекает
гармонический ток![]() и к которому приложе-
и к которому приложе-
80
но напряжение
![]() вила (4.1).
вила (4.1).
 Мгновенная
мощность равна
Мгновенная
мощность равна
![]() (4.27)
(4.27)
а после тригонометрических преобра- Рис.4.6
зований получим
![]() .
(4.28)
.
(4.28)
Как видно, мгновенная мощность изменяется
по гармоническому закону с частотой
![]() и содержит постоянную составляющую.
и содержит постоянную составляющую.
Средняя мощность равна
![]() ,
(4.29)
,
(4.29)
где
![]() - сдвиг фаз между напряжением и током.
Величину
- сдвиг фаз между напряжением и током.
Величину![]() называюткоэффициентом мощности.
называюткоэффициентом мощности.
Как видно, потребляемая двухполюсником
мощность определяется амплитудами
(действующими значениями) тока и
напряжения и коэффициентом мощности.
Для максимизации потребляемой мощности
(например, электродвигателем) необходимо
обеспечить условие
![]() ,
то есть нулевой сдвиг фаз между напряжением
и током (
,
то есть нулевой сдвиг фаз между напряжением
и током (![]() ).
Это означает, что двухполюсник должен
вести себя как сопротивление
).
Это означает, что двухполюсник должен
вести себя как сопротивление![]() .
.
В чисто реактивной цепи, содержащей
только индуктивности и емкости, сдвиг
фаз
![]() ,
при этом потребляемая мощность будет
рана нулю при любых амплитудах тока и
,
при этом потребляемая мощность будет
рана нулю при любых амплитудах тока и
81
напряжения.
Полученное выражение (4.29) для средней
мощности полностью согласуется со
значениями
![]() в элементах цепиR,LиC(табл. 4.1), так как в
сопротивлении
в элементах цепиR,LиC(табл. 4.1), так как в
сопротивлении![]() ,
а в индуктивности и емкости
,
а в индуктивности и емкости![]() .
.

4.3. Тригонометрический метод расчета
Тригонометрический метод расчета гармонических токов и напряжений в линейной цепи базируется на законах Ома и Кирхгофа для мгновенных значений сигналов в тригонометрической форме.
 В
качестве примера рассмотрим цепь на
рис. 4.7 при
В
качестве примера рассмотрим цепь на
рис. 4.7 при![]() ,
,![]() В,
В,![]() рад/с,
рад/с,![]() ,
,![]() кОм
и
кОм
и![]() нФ.
Обозначим гармонический ток
нФ.
Обозначим гармонический ток![]() в виде
в виде
Рис. 4.7
![]() ,
(4.30)
,
(4.30)
тогда с учетом свойств гармонических напряжений в сопротивлении и емкости на основе второго закона Кирхгофа получим
![]() .
(4.31)
.
(4.31)
82
Левая часть (4.31) может быть преобразована в тригонометрическую функцию,
![]() ,
(4.32)
,
(4.32)
тогда, уравнивая коэффициенты в правой и левой частях уравнения, получим
![]() ,
(4.33)
,
(4.33)
![]() .
(4.34)
.
(4.34)
Из полученных выражений нетрудно определить амплитуду и начальную фазу тока в цепи,
 А,
А,
![]() .
.
При найденном токе нетрудно определить
напряжение
![]() на емкости (проведите расчет
самостоятельно).
на емкости (проведите расчет
самостоятельно).
Как видно, тригонометрический метод требует суммирования гармонических функций с неизвестными параметрами, что приводит к громоздким расчетам, если число слагаемых функций более двух. Этот метод применим для расчета
очень простых цепей.
83
4.4. Векторная диаграмма цепи
 Гармонический
сигнал
Гармонический
сигнал![]() можно представить проекцией на
горизонтальную ось вектора, вращающегося
против часовой стрелки вокруг начала
координат с круговой (угловой) частотой
можно представить проекцией на
горизонтальную ось вектора, вращающегося
против часовой стрелки вокруг начала
координат с круговой (угловой) частотой![]() ,
как показано на рис. 4.8. Длина (модуль)
вектора равна амплитуде гармонического
сигнала
,
как показано на рис. 4.8. Длина (модуль)
вектора равна амплитуде гармонического
сигнала![]() и в момент начала вращения (при
и в момент начала вращения (при![]() )
угол его наклона к горизонтальной
)
угол его наклона к горизонтальной
Рис. 4.8 оси равен начальной фазе сиг-
нала
![]() (отсчет положительных значений проводится
против часовой стрелки).
(отсчет положительных значений проводится
против часовой стрелки).
Все гармонические токи и напряжения в
цепи с одинаковой частотой, равной
частоте источников сигнала, можно
представить совокупностью синхронно
вращающихся векторов вида рис. 4.8. Так
как все векторы вращаются синхронно и
между ними сохраняются амплитудные и
угловые соотношения, то вращение можно
остановить и рассматривать неподвижную
совокупность векторов. Если вращение
остановлено в момент времени
![]() ,
то угол наклона каждого вектора к
горизонтальной оси равен начальной
фазе соответствующего вектору
гармонического сигнала.
,
то угол наклона каждого вектора к
горизонтальной оси равен начальной
фазе соответствующего вектору
гармонического сигнала.

84
Для векторного представления гармонических сигналов выполняются законы Кирхгофав классической формулировке.
В качестве примера рассмотрим векторную диаграмму цепи, показанной на рис. 4.7. Результаты ее расчета тригонометрическим методом приведены в табл. 4.2 (проведите соответствующие расчеты).
Таблица 4.2
|
Сигнал |
Амплитуда |
Начальная фаза |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Векторная
диаграмма цепи приведена на рис. 4.9.
Векторы тока и напряжений построены по
данным табл. 4.2, длина вектора равна
амплитуде сигнала, а угол отклонения
от горизонтальной оси равен начальной
фазе (отсчет положительных значений
угла против часовой стрелки). Вектор
тока
Векторная
диаграмма цепи приведена на рис. 4.9.
Векторы тока и напряжений построены по
данным табл. 4.2, длина вектора равна
амплитуде сигнала, а угол отклонения
от горизонтальной оси равен начальной
фазе (отсчет положительных значений
угла против часовой стрелки). Вектор
тока![]() совпадает по направлению с вектором
напряжения
совпадает по направлению с вектором
напряжения![]() на сопротивлении, их длины (модули)
на сопротивлении, их длины (модули)
не одинаковы, так как масштабы Рис. 4.9
штабы (например, В/см и мА/см)
токов и напряжений различны (ток и напряжение не сравнимы между собой).
Напряжение на сопротивлении
![]() опережает по фазе напряжение на емкости
опережает по фазе напряжение на емкости![]() на 900. Это обусловлено тем, что в
на 900. Это обусловлено тем, что в
85
последовательной цепи рис. 4.7 через сопротивление и емкость протекает один и тот же ток, причем напряжение на сопротивлении совпадает по фазе с током, а на емкости – отстает по фазе от тока на 900.
Сумма векторов напряжений на сопротивлении и емкости в цепи рис. 4.7 по второму закону Кирхгофа (в векторной форме) равна ЭДС источника, что и показано на векторной диаграмме рис. 4.9.
Как видно, векторная диаграмма цепи может быть построена по результатам расчета всех гармонических токов и напряжений. Однако ее можно построить «качественно» (без знания точных параметров векторов, но с правильными соотношениями между ними) и не проводя численных расчетов.
 Рассмотрим
примерRCцепи, показанной
на рис. 4.10, в которой заданы положительные
направления и условные обозначения
всех токов и напряжений.
Рассмотрим
примерRCцепи, показанной
на рис. 4.10, в которой заданы положительные
направления и условные обозначения
всех токов и напряжений.
Прежде всего, необходимо проанализироватьструктуру цепи. В ней присутствует
Рис. 4.10 параллельный фрагмент (со-
единение
элементов CиR2),
который соединен последовательно с
сопротивлениемR1и источником напряжения![]() .
Тогда построение необходимо начать с
напряжения на параллельном фрагменте,
при этом
.
Тогда построение необходимо начать с
напряжения на параллельном фрагменте,
при этом![]() ,
этот вектор проведем произвольно по
модулю и направлению, например,
горизонтально, векторная диаграмма
показана на рис. 4.11.
,
этот вектор проведем произвольно по
модулю и направлению, например,
горизонтально, векторная диаграмма
показана на рис. 4.11.
Ток
![]() совпадает по фазе с напряжениями
совпадает по фазе с напряжениями![]() ,
а ток
,
а ток![]() опережает их по фазе на 900.
Соответствующие векторы изображены на
диаграмме рис. 4.11 с произвольной длиной
и указанными угловыми соотношениями
относительно вектора
опережает их по фазе на 900.
Соответствующие векторы изображены на
диаграмме рис. 4.11 с произвольной длиной
и указанными угловыми соотношениями
относительно вектора
86
![]()
 .
Векторная сумма этих токов по первому
закону Кирхгофа равна току
.
Векторная сумма этих токов по первому
закону Кирхгофа равна току![]() ,
то есть этот вектор строится исходя из
векторов
,
то есть этот вектор строится исходя из
векторов![]() и
и![]() .
Вектор напряжения
.
Вектор напряжения![]() на сопротивленииR1совпадает по направлению с вектором
тока
на сопротивленииR1совпадает по направлению с вектором
тока![]() и имеет произвольную длину, а вектор
ЭДС
и имеет произвольную длину, а вектор
ЭДС![]() по второму закону Кирхгофа Кирхгофа
равен Рис. 4.11
по второму закону Кирхгофа Кирхгофа
равен Рис. 4.11
сумме векторов
![]() и
и
![]() .
На этом построение «качественной»
векторной диаграммы цепи заканчивается.
.
На этом построение «качественной»
векторной диаграммы цепи заканчивается.
Если цепь содержит последовательный фрагмент, входящий в смешанное соединение, то построение целесообразно начинать с вектора тока этого фрагмента.
Векторная диаграмма электрической цепи может использоваться для иллюстрацииамплитудных и фазовых соотношений между токами и напряжениями, и для формированияаналитических выражений, связывающих их амплитуды (действующие значения) и начальные фазы.
Например, для диаграммы рис. 4.11 амплитуды
(действующие значения) токов
![]() ,
,![]() и
и![]() по теореме Пифагора связаны выражением
по теореме Пифагора связаны выражением![]() .
Для других соотношений можно использовать
теорему косинусов (пример приведите
самостоятельно).
.
Для других соотношений можно использовать
теорему косинусов (пример приведите
самостоятельно).
Для сложной цепи построение «качественной» векторной диаграммы требует вдумчивого подхода при выборе начального вектора и способов построения остальных векторов.
87
4.5. Особенности расчета цепи с гармоническими
сигналами
Мгновенные значения токов и напряжений в электрической цепи связаны между собой уравнениями законов Ома и Кирхгофа. Последние предполагают суммирование гармонических функций времени с неизвестными амплитудами и начальными фазами, например, с помощью теоремы косинусов, а это приводит к громоздким расчетам даже в относительно простых цепях.
Существенно упростить расчеты можно, отказавшись от описания сигналов с помощью тригонометрических функций времени и заменив его числами, на зависящими от времени. На эту возможность указывает векторная диаграмма цепи, которая полностью отражает свойства гармонических сигналов и не зависит от времени.
Известно, что вектор, выходящий из начала координат, можно представить комплексным числом. Таким образом, в теории электрических цепей при расчете гармонических процессов возникает метод комплексных амплитуд.
4.6. Расчет средней (потребляемой) мощности
По результатам расчета гармонических токов и напряжений можно определить мощность, потребляемую цепью от источника сигнала.
В качестве примера используем цепь на
рис. 4.7, результаты расчета приведены в
табл. 4.2. Рассматривая цепь относительно
зажимов источника как двухполюсник,
при амплитуде напряжения
![]() В,
тока
В,
тока![]() мА
и сдвиге фаз между ними
мА
и сдвиге фаз между ними![]() ,
получим
,
получим
![]() мВт.
мВт.
88
С другой стороны, в рассматриваемой цепи емкость не потребляет мощность гармонического сигнала, и она может выделяться только в сопротивлении. Тогда получим
![]() мВт.
мВт.
Как видно результаты совпадают.
Если в цепи имеется несколько сопротивлений, то общая потребляемая цепью мощность будет равна сумме мощностей, потребляемых каждым сопротивлением в отдельности.
4.7. Задания для самостоятельного решения
Задание 4.1. Тригонометрическим
методом определите амплитуды и начальные
фазы токов и напряжений на элементах
цепей, показанных на рис. 4.12, при![]() В,
В,![]() мА,
мА,![]() кОм,
кОм,![]() мГн
и
мГн
и![]() нФ.
нФ.

Рис. 4.12
По результатам расчета постройте полные векторные диаграммы цепей, проверьте выполнимость законов Кирхгофа.
Задание 4.2.Постройте «качественные» векторные диаграммы цепей, показанных на рис. 4.12. Сравните их с расчетными диаграммами из задания 4.1.
89
Задание 4.3.Определите мощность, потребляемую от источника сигнала в цепях, показанных на рис. 4.12. Проведите расчеты, рассматривая цепь как двухполюсник или выделив в ней энергопотребляющие элементы.
Задание 4.4.Постройте «качественные» полные векторные диаграммы цепей, показанных на рис. 4.13.

Рис. 4.13
Задание 4.5.Тригонометрическим
методом определите амплитуды и начальные
фазы токов и напряжений на элементах
цепи, показанной на рис. 4.10, при![]() кОм,
кОм,![]() нФ
и
нФ
и![]() В.
В.
Постройте полную векторную диаграмму цепи, сравните ее с приведенной на рис. 4.11. Определите мощность, потребляемую цепью от источника.
90
