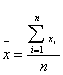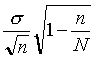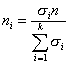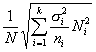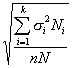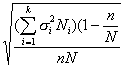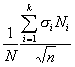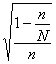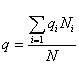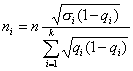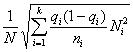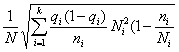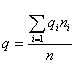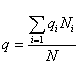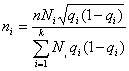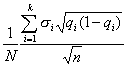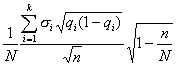Общая характеристика выборочного метода

Самый простой способ определения объема выборки из каждой типической группы, состоит в том, что объем всей намеченной выборки п делят на число типических групп k, т. е.

ni=n/k                         (5,6)

Второй, наиболее широко применяемый способ заключается в том, что объемы выборок из групп устанавливаются пропорционально объемам соответствующих типических групп, т. е.

В итоге для расчетов получается такая формула:

                            (5.7)

где ni — объем выборки из i-й типической группы; n — общий объем выборки из генеральной совокупности; Ni — объем i-й типической группы; N — объем генеральной совокупности.

Третий способ состоит в том, что число элементов в выборке для каждой типической группы определяется пропорционально средним квадратическим отклонениям соответствующих типических групп (?i), т. е. при определении ni руководствуются следующим соотношением:

 

Такой прием часто дает ощутимый выигрыш в точности. Сложность его использования состоит в том, что необходимо предварительно знать средние квадратические отклонения признака в типических группах, из которых будет извлекаться выборка. Для этого используются результаты расчетов по аналогичным данным либо делают пробные выборки из каждой группы и их средние квадратические отклонения кладут в основу расчета. Формула для расчета ni будет такой:

                             (5.8)

где σ_i, — среднее квадратическое отклонение i-й группы; 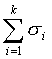 — сумма средних квадратических отклонений всех групп; n — объем выборки.

Наконец, четвертый способ образования типической выборки учитывает и размеры типических групп (Ni) и колеблемость признака в этих группах (?i); при формировании выборки исходят из того, что

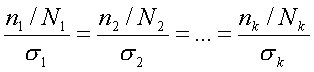
Формула для расчета ni, четвертым способом такова:

где Ni — объем i-й типической группы; ?i — среднее квадратическое отклонение i-й группы; n—общий объем выборки из генеральной совокупности; k— число типических групп.

Из указанных четырех способов определения численности выборок из типических групп самым простым, но и самым несовершенным является первый. Несложен для расчетов второй способ. Его целесообразно применять в тех случаях, когда типические группы резко отличаются по объему. Если типические группы имеют примерно одинаковый объем, то лучше формировать выборки с учетом рассеивания признака, т. е. третьим способом. Если, наконец, объемы типических групп различны и заметно отличны их средние квадратические отклонения, то наилучшие результаты достигаются при применении четвертого способа.

Рассмотрим теперь на примерах методику вычисления средних арифметических типических выборок и возникающих при этом стандартных ошибок.

Случайный отбор элементов из типических групп может проводиться двумя способами. Если типические группы в исходных данных разделены и каждая имеет собственную нумерацию, то случайный отбор элементов до нужного объема производится из каждой группы отдельно. Если же элементы типических групп расположены в генеральной совокупности вперемешку, как в нашем случае, то отбор осуществляется из всей совокупности, при этом следят, чтобы объемы отдельных групп не были превышены. Случайные числа, соответствующие элементам тех групп, объемы выборок по которым достигнуты, отбрасываются.

Пример 5. Из совокупности уставных грамот Тамбовской губернии сделать 10%-ную типическую выборку с учетом численности групп. Вычислить средний пореформенный надел на душу и среднюю ошибку выборки.

При знакомстве с уставными грамотами обращает на себя внимание тот факт, что надел земли на душу после реформы тяготеет к высшему душевному наделу. Естественно предположить, что типические группы, образованные с учетом размера высшего душевого надела, будут более однородными, чем вся совокупность в целом.

Разобьем всю совокупность на три группы. К первой группе отнесем селения с размером высшего душевого надела, равным 3,00 дес., ко второй — 3,25 дес., к третьей — 3,50 дес. Объемы групп будут равны соответственно 1717, 445 и 525 (Две грамоты мы не учитываем, так как в одной из них указан высший размер душевого надела, равный 2,0 дес., в другой—2,75 дес., в результате чего общий объем совокупности составил N1+N2+N3=2687 грамот.).

Получены следующие результаты расчетов средних характеристик по каждой из трех групп выборки:

для первой группы (высший душевой надел—3,00 дес.)

     

для второй типической группы (высший душевой надел — 3,25 дес.)

     

для третьей типической группы (высший душевой надел — 3,50 дес.)       

Пользуясь соответствующими формулами табл. 2, имеем окончательно:

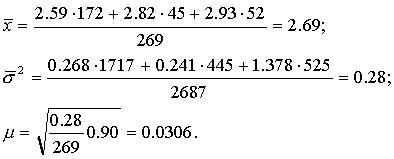
Средняя ошибка выборки, полученная таким способом, оказалась несколько меньше средней ошибки выборки, полученной при случайном отборе. В данном случае различие типических групп невелико. При больших различиях групп выигрыш в точности, даваемый типическим отбором, бывает более существенным.

Пример 6. Определить объемы выборок каждой типической группы так, чтобы они оказались пропорциональными средним квадратическим отклонениям соответствующих групп. Совокупность и общий объем выборки те же, что и в предыдущем примере.

Воспользуемся промежуточными результатами примера 5:

         

Тогда по формуле (5.8) объемы выборок типических групп будут такими:

  

т. е. из первой типической группы (высший размер душевого надела равен 3,00 дес.) следует отобрать 86 грамот, из второй типической группы (высший размер душевого надела — 3,25 дес.) — 81 грамоту, из третьей типической группы (высший размер душевого надела — 3,50 дес.) — 102 грамоты.

Пример 7. Генеральная совокупность и критерий, по которому происходит деление на типические группы, те же, что и в предыдущих двух примерах. Сделать типическую 10%-ную выборку, отбирая количество элементов в типических группах пропорционально численности этих групп и средним квадратическим отклонениям.

Рассчитать средний пореформенный надел на душу и среднюю ошибку выборки.

По формуле (5.9) численность выборок из типических групп будет следующей:

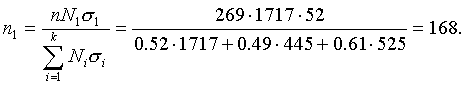
Аналогично рассчитываются n2 и n3: n2=41, n3=60.

Следовательно, из первой типической группы нужно взять 168 грамот, из второй — 41 грамоту, из третьей — 60. Отобрав требуемое количество грамот (техника отбора была изложена выше), переходим к вычислению интересующих нас характеристик.

Результаты расчета средних по группам следующие:

               

Соответствующие им средние квадратические отклонения равны:

              .

Средний по всей выборке пореформенный надел на душу равен (по формуле (5.5)):

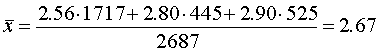
Для расчета средней ошибки выборки воспользуемся соответствующей формулой из сводной табл. 2:

Средняя ошибка выборки получилась меньше, чем при случайном методе отбора, но несколько больше соответствующей характеристики, полученной для типической выборки, образованной пропорционально численности типических групп. Последнее произошло, надо полагать, потому, что типические группы по размеру высшего душевого надела отличаются, в основном, по численности и значительно меньше—по разбросу признака.

Сведем воедино итоги рассмотренных примеров, чтобы еще раз сравнить полученные результаты (см. табл. 1).

В целом приведенные примеры подтверждают установленные в статистике общие положения. Важнейшим для применения выборочного метода в исторических исследованиях является то, что наиболее точные результаты дает типический отбор. Стандартная ошибка средней при этом методе отбора получается меньшей, чем при случайном и механическом отборе (сравним процентные отношения ошибок к средним арифметическим). При этом следует иметь в виду, что размеры наделов крестьян являются признаком, рассеивание которого является небольшим. При большей неоднородности изучаемых совокупностей данных преимущества типического отбора будут еще очевиднее. Что касается собственно случайного и механического отбора, то они в общем дают близкие результаты. Надо лишь всегда проверять, насколько механический отбор является близким к случайному. Принципиальных различий между бесповторным и повторным случайным отбором нет.

Для удобства пользования формулы выборочного метода, применяемые для вычисления выборочных средних арифметических и их стандартных ошибок при разных видах отбора, сведены в табл. 2. В эту таблицу не вошли формулы для расчета средних ошибок выборок при многоступенчатом способе отбора (Эти сведения можно найти в кн.: Йейтс Ф. Выборочный метод в переписях и обследованиях.). Что касается многофазного отбора, то он равносилен взятию выборок различных объемов для разных признаков и ничего нового в вычислительные процедуры не вносит.

Таблица 2. Формулы выборочного метода для средней арифметической при различных видах отбора.

	Выборочная средняя	Объем выборки из типических групп	Средняя ошибка выборки ?
			при повторном отборе	при повторном отборе
Собственно случайный отбор и механический отбор (При механическом отборе применяется формула бесповторной выборки, за исключением тех случаев, когда множителем  можно пренебречь.)
Типический отбор:  а) при равных объемах выборки из всех типических групп  б) при объемах выборки, пропорциональных средним квадратическим отклонениям типических групп
			Эти формулы являются одновременно и общим для всех случаев типического отбора
в) при объемах выборки, пропорциональных объемам типических групп
г) при объемах выборки, пропорциональных объемам типических групп и их средним квадратическим отклонениям

Таблица 3.Формулы выборочного метода для доли признака при различных видах отбора.

	Выборочная средняя	Объем выборки из типических групп	Средняя ошибка выборки ?
			при повторном отборе	При повторном отборе
Собственно случайный отбор и механический отбор (При механическом отборе применяется формула бесповторной выборки, за исключением тех случаев, когда множителем можно пренебречь.)
Типический отбор: а) при равных объемах выборки из всех типических групп б) при объемах выборки, пропорциональных средним квадратическим отклонениям типических групп
			Эти формулы являются одновременно и общим для всех случаев типического отбора
в) при объемах выборки, пропорциональных объемам типических групп
г) при объемах выборки, пропорциональных объемам типических групп и их средним квадратическим отклонениям

Средняя ошибка выборки для доли признака. Выборочный метод позволяет оценить не только среднюю арифметическую генеральной совокупности, но и долю некоторого (качественного или количественного) признака во всей совокупности.

Доля признака во всей совокупности (q) вычисляется как отношение числа элементов, обладающих этим признаком (No), к числу элементов всей совокупности (N), т. е. q=Nо/N.

Отметим, что рассмотренная выше теория и методика применения выборочного метода для расчета средней может быть применена и для расчета доли без каких-либо принципиальных изменений.

Сводка всех формул выборочного метода для доли признака дана в табл. 3.

Пример 8. На основе 10%-ной случайной бесповторной выборки из совокупности уставных грамот Тамбовской губернии вычислить доли селений с системой эксплуатации крестьян; а) оброчной, б) барщинной и в) смешанной, а также соответствующие им средние ошибки выборки

Из 264 грамот, составивших 10%-ную случайную бесповторную выборку, грамот, описывающих селения с оброчной, барщинной и смешанной системами эксплуатации, оказалось соответственно 51, 197 и 16 Тогда выборочная доля селений с оброчной системой эксплуатации равна  qоб=51:264=0,19, выборочные доли селений с барщинной и смешанной системами эксплуатации равны соответственно 0,75 и 0,06.

Воспользовавшись формулой для собственно случайной бесповторной выборки из табл. 3, рассчитаем средние ошибки выборки для доли:

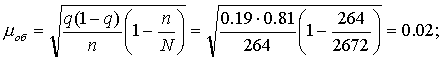
?б=0,03;  ?ом=0,01

Точность и надежность выборочного метода: предельные ошибки. Определение объема выборки

Предельная ошибка выборки и доверительный интервал. Средняя ошибка выборки дает некоторое представление об ошибке репрезентативности, т. е. об ошибке, с которой выборочная средняя представляет действительное значение генеральной средней. Именно она показывает, какова будет ошибка в среднем, если из одной и той же генеральной совокупности сделать много выборок одинакового объема. Однако в каждой конкретной выборке ошибка может существенно отличаться от средней ошибки, т. е. нет гарантии, что ошибка, которая действительно была допущена в конкретном выборочном исследовании, не превышает средней ошибки.

Поэтому гораздо полезнее было бы знать те границы, в которых «практически наверняка» находится действительная ошибка, допущенная в данной конкретной выборке. Эти границы (пределы) указываютсяпредельной ошибкой выборки (обозначим ее Δ). Предельная ошибка выборки показывает тот предел, которого практически наверняка не превосходит действительная ошибка. Иначе говоря, предельная ошибка Δ показывает действительно допущенную ошибку с избытком, с превышением (возможно, очень значительным) и тем самым гарантирует, что действительная ошибка не превосходит Δ.

Предельная ошибка Δ вычисляется на основе знания средней ошибки μ по формуле

                      (5,10)

где t — величина, вычисляемая по специальной таблице. Обратим внимание на то, что в определении предельной ошибки постоянно употреблялись слова «практически наверняка». Необходимо пояснить смысл понятия «практическая уверенность».

Установленный предел Δ для ошибки выборки лишь указывает, что если из генеральной совокупности сделать много выборок, то для подавляющего большинства из них ошибка выборки не превысит вычисленного нами предела Δ. При этом, правда, могут быть все-таки и такие выборки, у которых ошибка выборки больше Δ, и не исключено, что конкретная выборка входит в их число. Однако можно точно измерить степень уверенности в том, что ошибка конкретной выборки не превысит Δ. Для этого нужно указать долю выборок, у которых ошибка выборки не превосходит Δ. Обозначим эту долю выборок через Р, где . Чем ближе Р к единице, тем больше будет уверенность в том, что ошибка конкретной выборки не превышает Δ (Читатель, знакомый с понятием вероятности, заметит, что вместо слов «степень уверенности» можно использовать термин «вероятность».). На практике используются, например, значения, равные 0,68; 0,95; 0,99 и некоторые другие.

Значением Р фактически измеряется надежность результатов выборочного исследования: для значений Р, достаточно близких к единице, практически исключается возможность того, что генеральная средняя будет отличаться от вычисленной выборочной средней больше чем на Δ. Со своей стороны Δ указывает точность, гарантируемую заданным уровнем надежности Р. Таким образом, предельная ошибка выборки позволяет одновременно и взаимосвязано указать точность и надежность результатов выборочного исследования.

В математической статистике доказано, что распределение выборочных средних при достаточно больших n подчиняется нормальному закону (см. § 3, гл. 4) со средним значением, равным генеральной средней , и средним квадратическим отклонением, равным средней ошибке выборки μ. Значит, для достаточно больших выборок, вероятность Р того, что отклонение выборочной средней от генеральной средней не превысит по модулю предельной ошибки, т. е.   или 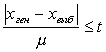 можно найти по табл. 1 приложения (где Ф(t) соответствует Р).

Эта же таблица позволяет решать и обратную задачу: по заданной вероятности Р найти величину предельной ошибки Δ, которая соответствует Р, другими словами, найти точность, соответствующую данному уровню надежности. Какова, например, предельная ошибка, соответствующая надежности 0,9545? По табл. 1 приложения найдем значение t, соответствующее вероятности Ф(t)= 0,9545. Оказывается, t=2. С вероятностью 0,9545 отклонение выборочной средней от генеральной по модулю не превосходит Δ=2μ, т. е. не выше двукратной средней ошибки выборки.

Разумеется, всегда желательно обеспечить большую надежность результатов, поэтому надо стараться выбрать Р возможно ближе к 1. Однако необходимо учитывать, что с возрастанием надежности увеличивается и t, а значит, и предельная ошибка Δ=tμ, т. е. падает точность результатов, что может оказаться по тем или иным соображениям недопустимым. Поэтому на практике приходится довольствоваться некоторым компромиссом между противоречивыми требованиями максимальной надежности и максимальной точности. Если такого компромисса достичь не удается и надежность и точность неудовлетворительны, следует сделать вывод, что объем выборки недостаточен и необходимо произвести новую выборку большего объема или же дополнить старую.

Знание предельной ошибки выборки позволяет указать и пределы для генеральной средней. Действительно, поскольку выборочная средняя   отличается от генеральной средней   (практически наверняка) не более чем на Δ, то

или, иначе,

                          (5.11)

Таким образом, с помощью вычисления выборочной средней и предельной ошибки выборки можно указать интервал, в котором практически наверняка находится генеральная средняя (так называемый доверительный интервал). При этом всегда указывается надежность Р этого результата (то значение Р, которое использовалось в вычислении Δ).

Пример 9. Вычислить предельные ошибки выборки по результатам примера 2 § 1 и определить пределы для генеральной средней.

Выборочная средняя для дореформенного надела равна 3,16, средняя ошибка выборки—0,0798.

Пусть Р=0,9545. Этому значению Р по табл. 1 приложения соответствует t=2. Пользуясь формулой (5.10), имеем Δ=2*0,0798=0,1596=0,16, т. е. предельная ошибка выборки равна приблизительно 0.16.

Переходим к определению пределов. Чтобы вычислить нижний предел, нужно из выборочной средней вычесть предельную ошибку выборки:

3,16—0,16=3,00.

Верхний предел получаем, прибавив к выборочной средней предельную ошибку:

3,16+0.16=3,32.

Тогда имеем следующие пределы для генеральной средней   :

Результаты можно интерпретировать так: с надежностью (вероятностью) 0,95 генеральная средняя будет не меньше 3,00 дес. и не больше 3,32 дес. Или, другими словами, если выборки повторять много раз, то в 95 случаях из 100 получим, что выборочная средняя будет отстоять от генеральной средней не далее, чем на величину вычисленной нами предельной ошибки, равной 0,16 дес.

Возьмем теперь Р= 0,9876=0,99. Тогда t=2,5,.

и генеральная средняя заключена в следующих пределах:

 .

Пределы для генеральной средней расширились, но зато увеличилась степень доверия к результатам: уже примерно в 99 случаях из 100 мы не ошибаемся, указывая эти границы для средней.

Как правило, в исторических исследованиях рассмотренный в примере уровень надежности (Р=0,95; P=0,99) оказывается достаточным.