Vektornaya_algebra

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное образовательное учреждение высшего профессионального образования

«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Крыштоп В.Г.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

По теме: «Введение в курс физики. Начала векторной алгебры»

для абитуриентов и студентов первого курса естественно научных факультетов

Р о с т о в – н а – Д о н у

2 0 0 8 г.

Методические указания разработаны кандидатом физикоматематических наук, доцентом кафедры общей физики В.Г. Крыштопом

Печатается в соответствии с решением кафедры общей физики физического факультета ЮФУ, протокол № 15 от 03.06.2008 г.

2

ВВЕДЕНИЕ

Физика - это основной раздел естественно научных знаний об окружающем нас мире. Физика как наука занимается установлением и описанием простейших (самых элементарных) взаимодействий в природе. В то же время такие естественнонаучные дисциплины, как химия, биология, геология и др., используют более сложные взаимодействия в своих исследованиях. Но только познав простейшие закономерности, можно уверенно себя чувствовать в исследовании других разделов науки. Это все и определяет физику как естественнонаучную основу знаний человечества.

Предлагаемое вниманию читателя учебное пособие предназначено для самостоятельной активной подготовки старших школьников по физике. Предполагается, что работая с данным пособием, читатель будет пользоваться как основной (учебники физики средней школы), так и дополнительной литературой по курсу элементарной физики, в которых читатель найдет нужный теоретический материал.

Для лучшего усвоения материала читать одни и те же разделы не менее двух раз. При первом чтении следует познакомиться с содержанием раздела, при повторном - выписывать основные положения, а затем обязательно устно пересказывать прочитанный материал. В каждом вопросе необходимо уметь выделить три момента:

1)вступление (с чего начинается ответ на вопрос);

2)главную или основную часть;

3)заключение (это прежде всего следствия и выводы, вытекающие из глав-

ной части).

Для лучшего усвоения следует составлять конспект; при этом в него следует записывать лишь самое главное: выводы формул, краткое и лаконичное пояснение сущности физического явления или процесса, формулировки законов, рисунки, схемы, подтверждающие либо иллюстрирующие изучаемый материал.

После усвоения теоретического материала учащийся может приступить к решению задачи. Решение задач по физике - хорошее средство применения теории на практике, причем, с одной стороны сам процесс решения помогает более глубоко и сознательно овладеть изучаемым материалом, с другой - знание теоретического материала - есть непременное условие умения решать задачи.

Методические указания к каждой теме и примеры решения задач данного пособия преследуют следующее:

1)пояснить применения изложенных методов;

2)углубить понимание физических законов;

3)развить умение рассуждать и сочетать знания из различных областей знаний физики.

3

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Пытаясь понять и объяснить определенный класс явлений, ученые часто прибегают к использованию модели. При этом под моделью понимается некоторый мысленный образ явления, опирающийся на уже известные понятия и позволяющий построить полезную аналогию. Например: а) материальная точка - всякое тело, обладающее массой, размерами которого в данной задаче можно пренебречь или более точно – математическая точка, обладающая массой; б) идеальный газ – это газ, состоящий из молекул, которые являются материальными точками и не обладают потенциальной энергией взаимодействия.

Ни одна модель не может быть безупречна, но может быть очень полезной и часто приводит к важным теориям (например, постулаты Бора для модели атома Резерфорда); однако не следует смешивать понятия модели или теории с реальной системой или самими явлениями.

Законы – некоторые краткие, но достаточно общие утверждения относительно характера явлений природы, которые выдержали экспериментальную проверку в широком классе наблюдаемых явлений.

Для количественного описания физических явлений необходимо ввести понятие физических величин, которые количественно определяются в сравнении с некоторыми однотипными величинами, условно принятыми за единицу данной величины (например: а) 1 метр это приблизительно 1/10000000 от 1/4 земного меридиана, проходящего через Париж, или более точно, длина, равная 1650763,73 длин волн в вакууме излучения, соответствующего переходу между уровнями 2p10 и 5d3, атома криптона-86; б) Сименс – электрическая проводимость проводника сопротивлением в 1 Ом).

Из всего многообразия физических величин необходимо выбрать некоторые (минимальное количество) в качестве основных, а все остальные считать производными.

Сейчас в мировой практике наибольшее распространение получила Международная система единиц физических величин – СИ. Она содержит 7 основных физических величин:

Таблица 1 Основные физические величины

1) Вектор

Для наглядного изображения векторов служат геометрические вектора, т.е. прямолинейные отрезки, имеющие не только определенную длину, но и определенное направление. Поскольку вектор есть направленный отрезок прямой, иногда,

изображаются отрезками, снабженными стрелками, указывающими их направление (рис. 1)

N

Рис. 1

Вектор полностью определяется заданием его длины (модулем) и направлением. Направление обычно определяется углом между вектором и осью либо углом между векторами.

Вектора могут быть

¾свободными (т.е. допускают параллельный перенос вектора в любую точку пространства),

¾скользящими (т.е. допускают скольжение (перенос) вектора вдоль прямой, совпадающей с вектором),

¾связанными (т.е. для таких векторов любые переносы запрещены);

¾коллинеарными два вектора (или более) называются коллинеарными, если они лежат на параллельных прямых;

¾компланарными три вектора (или более) называются компланарными, если они лежат в одной плоскости.

Для векторов на плоскости имеет место следующие свойство (без доказательства):

Любой вектор на плоскости можно разложить по двум данным неколлинеарным векторам этой плоскости единственным образом.

Для векторов в пространстве имеет место следующее свойство (без доказательства):

Любой вектор в пространстве можно разложить по трем данным некомпланарным векторам единственным образом.

Отметим, что разложение вектора на плоскости по двум неколлинеарным векторам и вектора в пространстве по трем некомпланарным векторам широко используется в физике, например, в задачах на движение тела брошенного под углом к горизонту; в задачах на применение закона сохранения импульса, в задачах динамики и статики, а так же во многих других.

6

2) Умножение вектора ( c ) на скаляр (а).

в два с половинной раза длиннее, сохранив прежнее направление

Пример 2. Даны вектор cv и а = -1; тогда вектор b = acr , т.е. умножение вектора c на (-1) меняет направление вектора на противоположное, т.е. вектор b по модулю равен вектору c , а направление его противоположно. Отсюда становится очевидным, что вектора всегда положительны.

Рис. 3

б) правило треугольника.

В этом случае от конца вектора a как от начала откладывается вектор b , и тогда суммарный вектор – это вектор, проведенный из начала первого вектора к концу второго вектора (рис.4а и 4б)

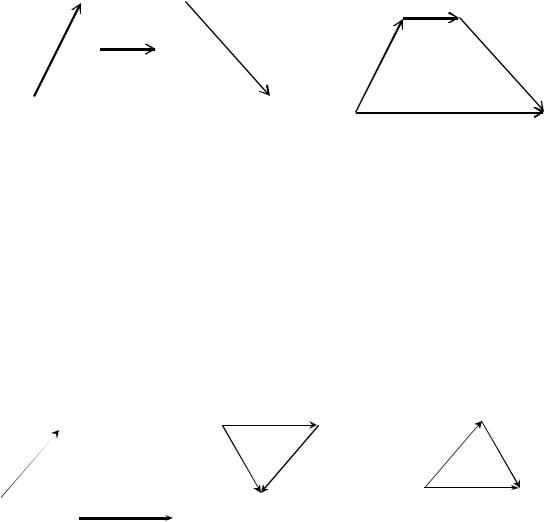
Это правило позволяет проще, чем правило параллелограмма, получить сумму трех и более векторов (см., например, рис. 5). В этом случае правило треугольни-

Рис. 5

ка называют правилом многоугольника

4) Вычитание векторов, b − ar.

Вектор ( −ar ) есть вектор, коллинеарный с вектором a ; модули этих векторов одинаковы, но направления их противоположны, сумма их ar + ( −ar ) = 0 Векторы ar и ( −ar ) называют равно-противоположными. ( 0 - это, так называемы, нуль-вектор, т.е. вектор, модуль которого равен нулю, а направление не опреде-

диагонали является разностью векторов. На приведенном чертеже (рис. 7) этот вектор равен разности веторов b и a ( d = b – a ).

8

ar cr

Рис. 7.

5) Разложение вектора на составляющие.

Если заданы два неколлинеарных направления, то любой вектор d , лежащий в одной плоскости с заданными направлениями, можно представить единственным способом в виде суммы двух векторов: d = d1 + d2 , где векторы d1 и d2 коллинеарные с заданными направлениями.

Для разложения вектора d необходимо через его начало провести прямые параллельные заданным направлениям; затем проделать такую же операцию для конца вектора d . В образовавшемся параллелограмме, диагональю которого явля-

ется вектор d , стороны этого параллелограмма являются искомыми векторами d1 и dr2 .

Например, для разложения d по заданным направлениям ab и ce построим a'b'|| ab и c'e'|| ce, затем через конец вектора d проводим a''b''|| a'b' и c''e''|| c'e'. В

образовавшемся параллелограмме вектора, построенные из общего начала на сто-

ронах ОВ и ОЕ являются искомыми векторами d1 и d2 , соответственно, тогда dr1 + dr2 = dr. (рис.8).

Рис.8

6) Проекция вектора на ось.

Проекцией (ах) вектора ar на ось Х называется длина отрезка отсекаемого на этой оси перпендикулярами, проведенными через концы вектора ar, взятая со знаком плюс (+), если направление от проекции начала вектора на ось к проекции его конца совпадает с положительным направлением оси, и со знаком минус (–) – в противоположном случае (рис. 9).

9

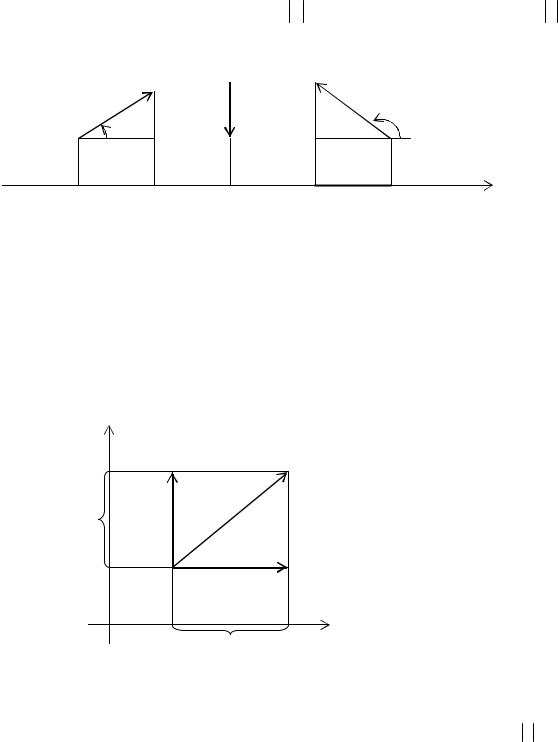
Обозначим угол между вектором и осью ОХ через α; тогда проекцию вектора a можно вычислить по формуле a x = ar cosα и соответственно cx = crcosα1 . При-

чем в этом случае соблюдается и правило знаков, т.е. если 0< α < π/2 , то cosα > 0 , а если π/2 < α1 < π, то cosα1 < 0 .

Рис. 9.

Совершенно очевидно, что если раскладывать вектора по двум взаимно перпендикулярным направлениям, например, по осям X и Y декартовой системы, то составляющие вектора по осям X и Y по модулю совпадают с проекцией вектора на соответствующую ось (рис. 10).

Поэтому принято записывать это следующим образом:

ar=arx +ary , где arx и ary – составляющие вектора a . Однако, этой же записи можно придать другой вид, если ввести понятие единичного вектора вдоль оси.

Y

Рис. 10

Единичным вектором оси (ортом оси) называется вектор er, направленный в положительную сторону оси, модуль которого равен 1, т.е. er = e =1.

Орт оси OX обозначают erx , а орт оси OY – ery .

Следовательно, любой вектор можно всегда задать через его проекции на оси де-

10