
Vektornaya_algebra
.pdf
картовой системы координат, т.е. a а{ах; ау}. Модуль вектора ar через проек-
ции по осям можно выразить по теореме Пифагора, т.е. ar =  ax2 + a2y .
ax2 + a2y .
7). Скалярное произведение двух векторов.
Скалярным произведением ar b двух векторов a и b называется произведе-
ние модулей этих векторов на косинус угла между ними (рис. 11):
ar· br = ( a , br ) = | ar|·| b |·cos( a , b ) = | a |·| b |·cosα = a·b·cosα
Скалярное произведение может быть записано через произведения проек-
ций этих векторов на оси прямоугольной системы координат: ar br = (ax erx + ayery )(bx erx + byery )= ax bx + ayby .
Доказательство этого соотношения проведите самостоятельно, предварительно рассмотрев скалярное произведение единичных векторов erx erx , ery ery и erx ery .
ar
 α = (ar,b)
α = (ar,b)
b
Рис. 11.
8) Векторное произведение двух векторов.
Векторным произведением двух векторов a и b называется новый вектор c , модуль которого равен произведению модулей перемножаемых векторов, умноженному на синус угла между ними, а направление этого вектора перпендику-
лярно плоскости, образованной векторами a и b и направлен в ту сторону, что-
бы поворот на наименьший угол от вектора |
а к вектору b |
вокруг полученного |
|
вектора cs происходил против часовой стрелки, если смотреть из конца вектора |
|||
cs. |
|
а и b обозначается |
|
Векторное произведение двух векторов |
|||
cs = аr ×b |
или |
c = [ а , b ] |
|
Из приведенного определения следует, что модуль вектора c |
равен |
||
│cs│= c = ab sin( а, b ).
Основные свойства векторного произведения.
1. При перестановке сомножителей векторное произведение умножается на (– 1), т. е. br ×аr = – ( аr ×br ); т.к. sinφ функция нечетная, следовательно,
11

sin( аr,br) = – sin(b , а).
Таким образом, векторное произведение не обладает свойством перестановки.
2. Векторное произведение обладает свойством сочетательности относительного
числового множителя; это свойство выражается следующими формулами:
λ ( аr ×br ) = (λа )×b = а ×(λb ).
3. Векторное произведение подчиняется распределительному закону, т.е. ( аr +br )×cs = ( а ×c) + (b ×c).
4. Векторное произведение равно нулевому вектору, если один из векторов является нулевым или если эти два вектора коллинеарны (т.е. эти вектора лежат на параллельных прямых).
Таким образом, условие коллинеарности двух векторов будет: аr ×b = 0
Векторное произведение двух векторов, заданных своими компонентами.
Обозначая через ax , ay , az компоненты вектора а , через bx , by , bz компоненты
вектора br , выразим через них векторное произведение вектора аr на вектор b :
аr ×br = (ax erx + ay ery + az ez ) × (bx ex + by ey + bz ez )
По свойству распределительности суммы векторов перемножаются как многочле-
ны. Следовательно, получаем: |
r |
|||
r |
r |
r |
r |
|
а |
×b |
= axbx ( ex |
×ex ) + ay bx ( ey ×ex |
) + azbx ( ez ×ex ) + |
|
|
+ axby ( erx ×ery ) + ayby ( ey ×ey ) + az by ( erz ×ery ) + |
||
|
|
+ axbz ( erx ×erz ) + aybz ( ey ×ez ) + azbz ( ez ×erz ). |
||
Так как вектора |
erx , ery , erz |
представляют три взаимно перпендикулярных еди- |
||
ничных вектора, то применяя правило векторного умножения двух векторов получим:
erx ×erx = 0r , |
ery ×ery = 0r , |
ez ×ez = 0 , |
ex ×ey = ez , |
ery ×erx = - ez , |
|||
erz ×erx = ery , |
erx ×erz = - ey , |
ey ×ez = ex , |
erz ×ery = - erx . |
||||
Следовательно, в полученном выражении векторного произведения пропадут три слагаемых, оставшиеся, объединяясь попарно, дают окончательную формулу
векторного произведения двух векторов:
аr ×br = (ay bz – az bx ) ex + (az bx – ax bz ) ey + (ax by – ay bx ) erz
Последнюю формулу можно также записать в символической, легко запоминающейся форме, если воспользоваться понятием определителя третьего порядка:
r |
r |
ex |
ey |
ez |
|
= ax |
ay |
az |
|||
а |
×b |
||||
|
|
bx |
by |
bz |
12

Замечание. В научной и учебной литературе принято обозначать единичные век-
тора декартовой системы координат не только как в нашем тексте, но и следую- |
|||
щим образом: |
erx = i , |
ery = rj , ez = k . |
|
9) Векторное произведение и теорема синусов |
|||
Площадь S |
треугольника АВС, образованного векторами ar, b , c , можно |
||
выразить через векторные произведения двух сторон треугольника (Рис. 12): |
|||
r r |
r |
r |
r |
2S = |[b, c ]| = |[ c |
, a |
]| = |[ a ,b ]| . |
|
Запишем модули векторных произведений через стороны и углы треугольника АВС (здесь использованы формулы приведения: sin (π - A) = sin A и, соответст-
венно, sin (π - B) = sin B, sin (π - C) = sin C):
b·c·sin A = c·a·sin B = a·b·sin C .
В
c
a
А  С
С
b
Рис. 12.
Поделив это выражение почленно на произведение сторон abc, получим фор мулу, выражающую теорему синусов для треугольника АВС:
sin A |
= |
sin B |
= |
sin C |
|
a |
b |
c |
|||
|
|
Отношение синуса любого угла треугольника к его противоположной стороне одинаково для всех сторон данного треугольника.
10) Смешанное произведение трех векторов.
Смешанным произведением трех векторов называется скалярное произведе-
ние вектора и векторного произведения двух других векторов. Варианты записи |
|||
этого произведения таковы: |
|
|
|
ar·[b , cr]=b ·[ cr, ar]= c ·[b , a ]=[ a b c ]=[ b c a ]=[ cr ar b ] |
|
||
При циклической перестановки векторов-сомножителей смешанное произве- |
|||
дение не меняется. |
|
|
|
Смешанное произведение [b , c ]· a это скалярная величина численно равная |
|||
объему параллелепипеда, построенного на векторах a , b , c , |
(Рис. 13). |
||
Формулу для смешанного произведения трех векторов |
r |
r |
r |
a |
·[ b |
, c ] можно так |
|
же выразить через компоненты векторов с помощью определителя третьего порядка:
a·[ br |
ax |
ay |
az |
, c ] = bx |
by |
bz = |
13

cx cy cz
= ax ( by cz – bz cy ) + ay ( bz cx – bx cz ) + az ( bx cy – by cx ).
[ b , cr]
ar
θ
b
cr
V = S·h = |[ b , c ]|·a·cos β
Рис. 13
Следствие: Если вектора a , b и c лежат в одной плоскости (т.е. являются компланарными), то смешанное произведение трех векторов равно нулю. Это следует из геометрического смысла смешанного произведения трех векторов, указанного выше, а именно, оно равно объему параллепипеда, построенного на этих трех векторах. Объем параллепипеда, построенного на трех векторах, лежащих в одной плоскости, очевидно, равен нулю.
Отсюда можноr сформулировать условие компланарности трех векторов:
Три вектора a , b и c компланарны, если их смешанное произведение равно нулю.
Некоторые важные приложения к векторной алгебре.
Приложение 1. |
Проекция вектора на заданное направление. |
||
Пусть направление задано вектором: |
l = lx ex + ly ey + lz erz ) |
||
Найти проекцию вектора |
a = ax ex + ay ey + az ez на заданное направление l . |
||
Проекция вектора |
a |
на направление |
l может быть найдена из скалярного |
произведения векторов a |
и lr: |
|
|
r |
|
|
|
l ·a = l·аl . |
|
|
|
Подставляя выражение для скалярного произведения векторов получим :
аl = |
ar lr |
= |
|
ax lx + ay ly + az lz |
. ▲ |
|
|
|
|||||
|
||||||
|
l |
|
lx2 + ly2 + lz2 |
|||
Приложение 2. Теорема косинусов в векторной алгебре. |
||||||
Пусть вr |
треугольнике АВС (Рис. 14) стороны ВС = a, АС = br, АВ = c ; |
|||||
так что |
a = b |
– c . Вычислим выражение: |
||||
|
|
|
|
a ·a = а2 = ( br– c)·(b – c ). |
||
|
|
|
14 |
|||
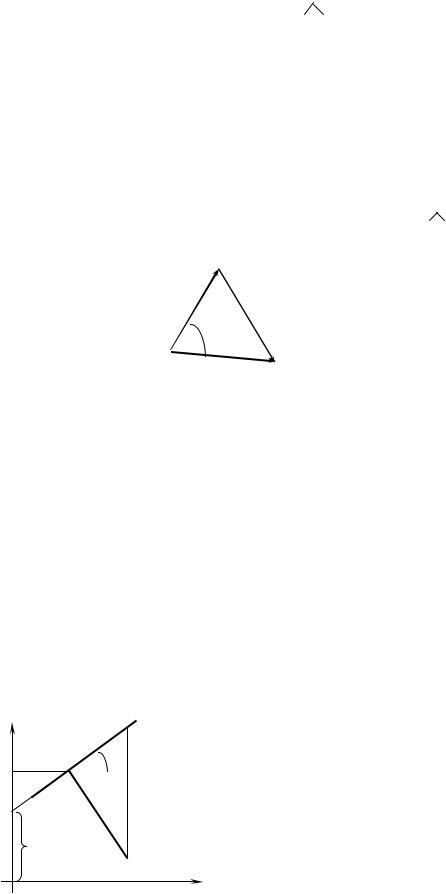
b2 + c2 – 2( ·b) = b2 |
+ c2 – 2bc·cos( |
,b), то есть |
|
|
В |
|
|
|
c |
a |
|
А |
αr |
|
С |
|
b |
|
|
Рис. 14.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Приложение 3. Расстояние от точки до прямой.
Пусть прямая задана уравнением: y = kx + b (где k = tgα, b = yo – xo·tgα), а точка А своими координатами xА, yА. Далее, АН – перпендикуляр, опущенный на заданную прямую, длину которого h нам нужно найти. Проведем прямую, параллельную оси «у» через точку А до пересечения с заданной прямой в точке В. При этом абсциссы этих точек одинаковы, т.е. хА = хВ, а ординату точки В можно найти по уравнению прямой : уВ = kхА + b .
y |
(хА, kxА + b) |
В |
|
α |
|
Н |
|
b |
h |
А (xA, yA) |
|
||
|
|
x |
|
Рис. 15 |
15 |
|
|

Тогда расстояние h можно найти из прямоугольного треугольника АВН :
h = АВ·cos = | kхА + b – уА |· cosα ,
Где α – угол наклона прямой к оси абсцисс. Косинус этого угла можно выразить
через коэффициент прямой - k, |
т.к. |
он равен |
tgα. Для этого разделим обе части |
||||||||
основного тригонометрического тождества |
|
|
|
|
|
||||||
|
cos2α + sin2α = 1 |
|
|||||||||
cos2α и получим : 1 + tg2α. = |
1/cos2α , откуда следует: |
||||||||||
cos2 α = |
1 |
|
= |
|
|
1 |
. |
||||
1 + tg2α |
|
|
+ k2 |
||||||||
|
|
|
|
1 |
|
||||||
Окончательно имеем: |
|
|
kxA + b − yA |
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||
h = |
. ▲ |
||||||||||
|
1 + k2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
Приложение 4. Определитель третьего порядка
Определителем называется числовое значение квадратной матрицы, содержащей одинаковое число столбцов и строк. Определитель активно используется в математике в теории решения систем линейных уравнение и во многих разделах физики как, например, в нашем случае при расчете векторного произведения двух векторов и смешанного произведения трех векторов. Не рассматривая общую теорию расчета определителей. Рассмотрим только определитель третьего порядка.
Определитель (детерминат) третьего порядка квадратной таблицы (матрицы 3×3) с девятью числами (элементами) обозначается: как D или det [aik], где символ «i» обозначает номер строки, а символ «k» обозначает номер столбца, - является алгебраическим выражением или числом, записанных определенным образом.
|
a11 |
a12 |
a13 |
|
|||
D = det [aik] = |
a21 |
a22 |
a23 |
|
a31 |
a32 |
a33 |
|
|
|
|
Определитель (детерминат) третьего порядка равен сумма шести членов (3!
– 3 факториал), каждый из которых представляет собой произведение трех элементов матрицы, взятых по одному из каждой строки и каждого столбца, т.е.
∑(−1)r a1k1 a2k2 a3k3 ,
где r число парных инверсий элементов из трех (k1, k2, k3). Если k1> k2, то инверсия равна 1, если нет, то равна нулю. Аналогично, если k1> k3 и k2> k3. Сумма инверсий в каждом члене суммы равно r .
16

Введем некоторые важные определения для матрицы третьего порядка –
элементы а11 , а22 , а33 образуют главную диагональ матрицы (определителя); элементы а13 , а22 , а31 образуют побочную диагональ матрицы (определителя).
Можно заметить, что подобные определения справедливы для квадратных матриц любого порядка.
Фактическое вычисление определителя третьего порядка по его элементам легко выполняется с помощью некоторых простых правил.
Первое правило. (Добавление столбцов) Перепишем таблицу определителя D и припишем справа еще раз два первых ее столбца; таблица примет вид:
|
а11 |
а12 |
а13 |
а11 |
а12 |
|
а21 |
а22 |
а23 |
а21 |
а22 |
|
а31 |
а32 |
а33 |
а31 |
а32 |
– |
– |
– |
+ |
+ |
+ |
Численное значение определителя третьего порядка равно алгебраической сумме шести слагаемых; причем, со знаком (+) плюс возьмем те три произведения стоящих на главной диагонали, а так же на двух параллельных к ней (на схеме подчеркнуты сплошной линией). Произведения же элементов, стоящих на побочной диагонали и на двух параллельных к ней, возьмем со знаком (–) минус (на схеме перечеркнуты пунктирной линией). Написав эти произведения подряд получим выражение для определителя третьего порядка:
|
a11 |
a12 |
a13 |
|
|
|
|
|
|
|
D = det [aik] = |
a21 |
a22 |
a23 |
= |
а11 а22 а33 + а13 а21 а32 + а12 а23 а31 |
– а13 а22 а31 – |
||||
|
a31 |
a32 |
a33 |
|
|
– а12 а21 а33 – а11 а23 а32 . a11 a12 |
a13 |
|||
Например: |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
D = det [aik] = |
3 |
–2 |
5 |
3 |
–2 |
5 |
3 |
–2 |
|
|
7 |
4 |
–8 |
= 7 |
4 –8 |
7 |
4 = 3·4·(-4) + (-2)·(-8)·5 + 5·7·(-3) – |
||||
|
5 –3 |
-4 |
|
5 –3 -4 |
5 –3 |
|
||||
– 5·4·5 – 3·(-8)·(-3) – (-2)·7·(-4) = -48 + 80 – 105 – 100 – 72 – 56 = -301
Второе правило. (Правило треугольника) В этом случае положительные слагаемые определяются следующим образом – первое, это произведение трех членов матрицы стоящих на главной диагонали (а11·а22·а33), два других, это произведение трех членов матрицы расположенных в вершинах треугольника, основание которого параллельно главной диагонали. Таких треугольника два (а12·а21·а33) и (а11·а23·а32). В матрице определителя эти треугольники выделены сплошными линиями.
a11 |
a12 |
a13 |
a11 |
a12 |
a13 |
a11 |
a12 |
a13 |
a11 |
a12 |
a13 |
D = a21 |
a22 |
a23 |
= a21 |
a22 |
a23 |
= a21 |
a22 |
a23 |
= a21 |
a22 |
a23 |
17
a31 a32 a33 |
a31 a32 a33 |
a31 a32 a33 |
a31 a32 a3 |
Отрицательные слагаемые определяются следующим образом – первое, это произведение трех членов матрицы стоящих на побочной диагонали (а13·а22·а31), два других, это произведение трех членов матрицы расположенных в вершинах треугольника, основание которого параллельно побочной диагонали. Таких треугольника два (а12·а21·а33) и (а11·а23·а32). В матрице определителя эти треугольники выделены пунктирными линиями. Соединив все слагаемые воедино получим уже знакомую формулу.
Третье правило. (Добавление строк) Аналогично первому; только добавляются не столбцы, а первые две строки приписываются снизу. Предлагается сформулировать это правило самостоятельно и проверить его.
Основные свойства определителя.
¾1. Величина определителя det[aik] не меняется, при замене строк столбцами или наоборот – столбцов строками (что соответствует перемене местами индексов i и k)
¾2. Определитель det[aik] равен нулю, если соответствующие элементы каких либо двух строк (или столбцов) равны или же пропорциональны.
¾3. Умножение всех элементов какой либо строки (или столбца) определителя det[aik] на множитель β равносильно умножению определителя на β.
¾4. При перестановке двух любых строк (или столбцов) определитель det[aik] меняет знак на противоположный.
¾5.Определитель det[aik] равен нулю, если все элементы какой либо строки (или столбца) равны нулю.
¾6. Величина определителя det[aik] не меняется при прибавлении к элементам строки (или столбца) соответствующих элементов какой либо
другой строки (или столбца), умноженных на одно и тоже число γ. Эти свойства относятся к определителям любого порядка
|
|
|
|
|
ПРИМЕРЫ РЕШЕНИЯ. |
|
|
|
|
|
|
|
|
|
|
|
1. Найти сумму векторов: |
|
a · br + b · c + c · a, если a = b = c = 1 |
|
и |
|
a + b + c |
||||||||||
= 0. |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
Решение 1: Вычислим квадрат суммы векторов: ( a + |
|
2 |
= a |
2 |
+ b |
2 |
2 |
|||||||||
b + c ) |
|
|
|
+ c + |
||||||||||||
r |
r |
r |
r |
|
r |
|
|
|
|
|
|
|
|
0 = 3 + |
||
2 a |
· b |
+ 2 b |
· c |
+ 2 c · a. С учетом условия задачи получим: |
|
|||||||||||
r |
r |
r |
r |
r |
r |
r |
|
|
r |
|
r |
|
|
3/2.▲ |
||
( a |
· b |
+ b · c + c |
· a), откуда следует, что a · b |
+ b |
· c + |
c |
· a = – |
|||||||||
Решение 2: Из равенства суммы векторов нулю следует, что данные векторы образуют замкнутый треугольник. Поскольку модули векторов одинаковы, то треугольник правильный, с углами при вершинах равнымиr60О , соответственно углы между векторами равныr 120О. Поэтому a · b = b · c = c · a = 1·1cos 120О = – 1/2 , а a · b + b · c + c · a = – 3/2 .▲
18

2. Проверить компланарны ли векторы: a{1; -1; 2}, b {-2; 0; 1}, c {5; |
-1; |
0}? |
|
|||||||||||||
Решение 1. |
Используем известное условие компланарности трех векторов: |
|||||||||||||||
r |
|
r |
r |
|
|
|
выполняется ли это условие для наших |
|||||||||
a ·(b |
× c ) = 0. Для проверки |
|||||||||||||||
трех векторов, вычислим их смешанное произведение, рассчитав оп- |
||||||||||||||||
ределитель третьего порядка: |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
ax |
ay |
az |
|
1 -1 2 |
|
1 -1 2 1 -1 |
|
|
|
||||
|
a·(br× c ) = bx |
by |
bz |
= -2 0 1 = -2 0 1 -2 0 = |
|
|
||||||||||
|
|
|
cx |
cy |
cz |
|
5 -1 0 |
|
5 -1 0 5 -1 |
|
|
|
||||
1·0·0 + (-1)·1·5 + 2·(-2)·(-1) – 2·0·5 – 1·1·(-1) – (-1)·(-2)·0 = 0 –r |
5 + 4 – – 0 |
|||||||||||||||
+ 1 – 0 = 0. Т.к. определитель равен нулю, то вектора |
a ,b |
|
и c ком- |
|||||||||||||
планарны.▲ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение 2. Среди векторов a{1; -1; 2}, b {-2; |
0; |
1}, |
c {5; |
-1; |
0} нет колли- |
|||||||||||
неарных, так как компоненты одного из них не пропорциональны |
||||||||||||||||
компонентам любого из оставшихся двух. |
Если |
вектор |
|
c {5; |
-1; |
|||||||||||
0} сможем разложить по векторам a |
и |
b , |
то векторы a, |
b |
и |
c |
||||||||||
компланарны (см. |
свойства векторов, стр. 6.). Если |
же вектор |
c |
|||||||||||||
нельзя разложить по векторам a и |
b , |
то векторы |
a, |
b |
и |
c не |
||||||||||
компланарны. Таким образом, для решения задачи нужно устано- |
||||||||||||||||
вить, можно ли вектор c |
разложить по векторамra и |
br, то есть су- |
||||||||||||||
ществуют ли такие числа µ и λ, что |
c = µ a + λb |
или запишем это |
||||||||||||||
равенство через компоненты векторов |
a, |
b |
и c : |
|
|
|
|
|
|
|||||||
5 erx |
– ey + 0· erz |
= µ ex – µ ey |
+ µ 2 ez |
+ λ (-2) ex + λ 0 ery + λez |
. Так |
|||||||||||
как численные коэффициенты при соответствующих единичных векторах в левой и правой частях уравнения должны быть равны, то по-
лучаем три уравнения: |
|
5 = µ – 2λ |
|
–1 = – µ |
, |
0 = 2µ + λ |
|
как видим, в данном случае, система имеет решение: µ r= 1; λ = -2. |
||
Поэтому вектор |
c можно разложить по векторам a |
и b , т.е. c = a – |
r |
r |
|
2 b , и, следовательно, векторы a ,b и c компланарны.▲
3.Лежат ли точки А, В и С на одной прямой, если заданы их координаты: А(3; -7; 8), В(-5; 4; 1), С(27; -40; 29).
Решение. Если точки А, В и С лежат на одной прямой, то любые два вектора построенные на этих точках коллинеарны и, соответственно, их компоненты равны или пропорциональны. Например, рассмотрим
19
|
|
uuur |
и |
uuur |
. Найдем компоненты этих векторов: |
uuur |
11; |
||||
вектора АВ |
АС |
АВ {-8; |
|||||||||
-7} |
и |
uur |
|
-33; |
|
uur |
= –3 |
uur |
, поэтому вектора |
uur |
|
АС {24; |
21}. Очевидно, АС |
АВ |
АВ |
||||||||
и |
uuur |
коллинеарны, |
и, следовательно, |
точки |
А, В и |
С лежат на |
|||||
АС |
|||||||||||
одной прямой.▲ |
|
|
|
|
|
|
|
||||
4. Лежат ли точки |
A, B, C и D |
в одной плоскости, если они имеют координа- |
|||||||||
ты: A(-9; 4; |
7), |
B(3; |
-6; -1), |
C(-5; 5; 10) и D(-7; |
15; |
0)? |
|
|
|||
Решение: Если точки A, B, C и D лежат в одной плоскости, то три вектора |
|||||||||
построенные на этих точках должны лежать в одной плоскости. На- |
|||||||||
пример, выберем векторы |
|
uur |
uur |
uur |
|||||
AB {12; -10; -8}, |
AC {4; 1; 3} и |
AD {2; |
|||||||
11; |
0}. Далее задача сводится к уже рассмотренной раннее (пример |
||||||||
2). Воспользуемся первым решением, т. е. проверим чему равно сме- |
|||||||||
шанное произведение выбранных трех векторов: |
|
||||||||
uuur |
uuur |
uuur |
12 -10 -8 |
|
|
|
|
||
4 |
1 |
3 |
|
= 0 – 352 – 60 + 16 + 396 – 0 = 0. |
|
||||
AB ·( AC |
× AD ) = |
|
|
||||||
|
|
|
2 |
11 |
0 |
|
|
|
|
Следовательно, |
точки A(-9; |
|
4; 7), B(3; -6; |
-1), C(-5; 5; 10) |
и D(- |
||||
7; |
15; |
0) лежат в одной плоскости. ▲ |
|
|
|||||
20
