3. Условия квадрируемости фигур

Теорема 1. Чтобы плоская фигура F была квадрируема необходимо и достаточно, чтобынашлись плоские многоугольные фигурыP, Q: , для которых выполнено. (2)

Доказательство.

1) Необходимость.

Пусть F – квадрируема . (3)

На основании свойств верхней и нижней грани :

(4)

(5)

Из (4) и (5), учитывая (3), получим

.

В силу (3) отсюда следует (2).

2) Достаточность.

Пусть , для которых.

Из (1) и (2) следует . Так как- произвольное положительное число, то. Следовательно, по определению 12,F- квадрируема.

Теорема 2.(обобщение теоремы 1) Для того, чтобы плоская фигура F была квадрируема необходимо и достаточно, чтобы нашлись две квадрируемые фигуры, такие, что.

Определение 13. Множество точек плоскости К имеет площадь нуль, если это множество можно заключить в многоугольную фигуру со сколь угодно малой площадью.

многоугольная фигура F: , такая, что .

Теорема 3. Для квадрируемости фигуры F необходимо и достаточно, чтобы её граница имела площадь 0.

Доказательство.

1) Необходимость.

П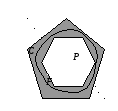устьF – квадрируема. Докажем, что . Зафиксируем. Т. к.F квадрируема, то , для которых(по теореме 1). Многоугольная фигура Q\P содержит границу фигурыF. Так как , то. Тогда по определению 13.

2) Достаточность.

Пусть . Тогда по определениюнайдется многоугольная фигураС: , для которой. Не умаляя общности доказательства, можно считать, что многоугольная фигураС не содержит в себе целиком F. Тогда из точек фигуры F, не попавших в С, составится многоугольная фигура Р, содержащаяся в F. Если к Р присоединить С, то получится многоугольная фигура , которая содержитF. Так как , то по теореме 1 фигураF квадрируема.

P

P

4. Кривые с нулевой площадью

Теорема 4. Кривая Г, заданная уравнением ,или уравнением вида, где, имеет площадь 0.

Доказательство.

Проведём для кривой Г: . Фиксируем. Так как, то она равномерно непрерывна на. Следовательно, для числа(6)

выполнено . (7)

Р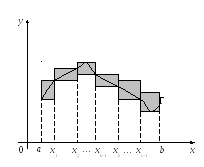азобьёмна частичные отрезки. В силу непрерывностиf на , а, значит, и на каждом частичном отрезке, она имеет на нем наименьшее и наибольшее значения. То есть:,. Т.к., то. Значит, для точекивыполняется неравенство (6). Тогда согласно (7). Заключим кривую Г в ступенчатый многоугольник, состоящий изn прямоугольников . Найдём его площадь.

.

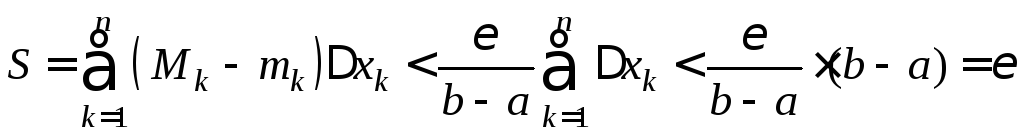По определению 13 .

Теорема 5. Плоская фигура F квадрируема, если её граница состоит их конечного числа частей, каждая из которых представляет собой кривую, определяемую уравнением видаy=f(x), a≤x≤b или x=φ(y), c≤y≤d, где fC[a;b], φC[c;d].

Доказательство.

Каждая из частей границы имеет по теореме 4 площадь 0. Но частей конечное число. Следовательно, . Тогда по теореме 3 фигураF квадрируема.

5. Свойства площади

Т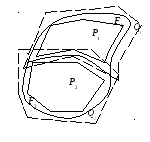еорема 6 (аддитивность площади). Если фигура F разбита на две квадрируемые фигуры ибез общих внутренних точек, то фигураF квадрируема и . (8)

Доказательство.

Так как иквадрируемы, то,. Но . Следовательно, F квадрируема. Докажем равенство (8).

Зафиксируем . Так какиквадрируемы, то

1), (9)

2). (10)

Рассмотрим многоугольные фигуры и. Ясно, что. Т. к., то. Но.

Так как , то выполняется условие:

. (11)

Т.к. ,

,

то, сложив эти неравенства, получим

. (12)

Из (9),(10) следует что

.

Тогда из (11), (12) получаем, что числа инаходятся между одними и теми же, причем сколь угодно близкими, границамии. Следовательно,. Отсюда следует равенство (8).

Теорема 7 (монотонность). Если - квадрируемые фигуры, то.

Теорема 8 (инвариантность). Если , то.

Доказательство следует из инвариантности площади многоугольной фигуры и определения площади плоской фигуры через площадь многоугольной фигуры.

Лк (2ч)