1.7.Метод парабол

Метод минимизации, называемый методом парабол, является аналогом известного метода решения уравнений с одним неизвестным, называемого методом касательных.

Пусть на определена трижды дифференцируемая функция, причем,на,,.Тогда функция будет иметь наединственную точку глобального и локального минимума. В этой точке производная обращается в, вторая производная- положительна. Поэтому для отыскания точки минимумамы будем решать уравнениена.

Легко видеть, что выполняются все условия применимости метода касательных, применительно к решению уравненияна(насуществует единственный кореньуравнения,и непрерывны и не обращаются вна). Этот метод позволяет определить приближенное значение точки минимумас погрешностью, не превышающей заданного положительного числа.

Для решения уравнения настроится последовательность приближений. В начале задается начальное приближение,, еслина. В противном случае, когда на,. Остальные члены последовательности вычисляются по рекуррентной формуле:

, (6)

Так строится последовательность приближений к точке минимума 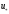в методе парабол. Вычисления по формуле(6) продолжают до тех пор, пока не будет выполнено условие окончания итераций:

(7)

Здесь - положительное число такое, чтона. После выполнения условия (7) вычисляется приближенное значение точки минимума

(8)

Замечание

Существует еще одна алгоритмическая схема метода касательных. Она применяется в случае, когда значения производных ивычисляются по очень громоздким формулам или их вообще трудно найти. Последовательность приближений в данном случае вычисляется следующим образом:

1.8. Метод золотого сечения

Пусть имеется функция одной переменной, непрерывная на, имеющая на этом отрезке единственную точку локального минимума (совпадающую с точкой глобального минимума). В этом случае метод золотого сечения позволяет получить приближенное значениекоординаты точки глобального минимумас погрешностью, не превышающей заданного положительного числа, а также приближенное значениеэтого минимума.

Метод золотого сечения представляет собой итерационный метод,подобный методу равномерного перебора и половинного деления. Процесс получения приближенного решения представляет собой последовательность однотипных шагов.

рис. 8.1.

Шаг 1.Разобьем на три, вообще говоря,неравные части точками()так, чтобы первый и третий отрезки разбиения имелиодинаковую длину, а отношение их длин к длине всего отрезка имело заданное значение (см. первую числовую ось рисунка8.1):

(9)

Найдем наименьшее из значений функции в точках()и точки, в которых это значение достигается.

Если это значение достигается функцией в точках или, то отбросим отрезок, а в противном случае – отрезок.

Шаг 2.С выбранной оставшейся после отбрасывания частью мы поступим так же как со всем отрезком на первом шаге, то есть разобьём её на три подобных части. Для координат точек разбиения оставим старые обозначения (). Таким образом, при каждом новом разбиениивыбранной части последнего отрезка, значения переменных будут соответствующим образом меняться. На второй и третьей числовой оси рисунка 8.1 показаны два таких разбиения выбранной части отрезка. Потребуем также, чтобы для каждого нового разбиения выбранной части отрезка выполнялось условие(9) при постоянном значении величины .

Далее, так же как и на первом шаге, находится наименьшее из значений функциив точках ()и отбрасывается один из полученныхотрезков разбиения. Второй шаг на этом заканчивается. Последующие шаги аналогичны предыдущим.

Шаги метода продолжаются до тех пор, пока не будет выполнено условие:

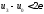(10)

После этого, в качестве приближенного значения координаты точки глобального минимума выбирается середина последнего отрезка разбиения:

(11)