1.3. Метод равномерного перебора. Условие Липшица.

При обосновании этого численного метода минимизации используется условие Липшица.

Определение 3.1.

Говорят, что функция удовлетворяет условию Липшица нас константой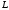, если для любыхиизвыполняется

(1)

Величина при этом называетсяконстантой Липшица.

рис. 3.1.

Геометрический смысл условия Липшица состоит в том, что модуль тангенса угла наклона () любой секущей графика функции, проходящей через точкии, не превышает(рис. 3.1.).

Теорема 3.1.

Если функция удовлетворяет условию Липшица на, то она непрерывна на.

Следствие 3.1.

Если функция удовлетворяет условию Липшица на, то существует хотя бы одна точка минимума функциина.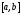

Теорема 3.2.

Пусть функция дифференцируема наи существует конечная точная верхняя грань модуля производной этой функции. Тогда функцияудовлетворяет условию Липшица нас константой.

Описание метода

Пусть функция удовлетворяет условию Липшица нас известной константой. Тогда, согласно следствия из теоремы 4.1, будет существовать минимуми хотя бы одна из точек минимумафункции на. Будем искать приближения для минимумаи какой-нибудь точки минимумафункциина() с погрешностями, не превышающими заданного положительного числа.

Для решения поставленной задачи разобьем наравных по длине отрезков.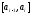

Здесь ,;. Обозначим середины этих отрезков. Вычислим значения функции в серединах отрезков разбиения() и найдем. Далее определим какой-нибудь номертакой, что значение(- наименьшее среди значений функции:). После этого выберем в качестве приближений дляизначенияи.

Чтобы использовать описанный алгоритм отыскания приближений минимума и точки минимума необходимо установить как по заданному значению оценки погрешности подобрать значение, при котором полученные таким способом приближения будут иметь заданную точность. На этот вопрос отвечает следующие теоремы.

Теорема 3.3.

Пусть функция удовлетворяет условию Липшица нас известной константой. Если, то.

Теорема 3.4.

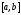Пусть функция удовлетворяет условию Липшица нас известной константой. Еслии, то, и, и.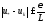

1.4. Метод последовательного перебора

Обозначим через класс функций, удовлетворяющих условию Липшица на отрезке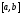, с одной и той же для всех функций этого класса константой. Для функции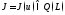будем рассматривать задачу минимизации первого типа, когда ищется величина.

На классе можно предложить простой и эффективный последовательный метод перебора, когда выбор точки при каждом производится с учетом вычислений значения функции в предыдущих точкахи задачу: как выбрать числои метод, чтобы

(2)

удается решить за меньшее количество вычислений значений функции. Положим

(3)

где ,, ,а число определяется условием.

Теорема4.1.

Метод последовательного перебора (3) решает задачу (2) на классе .

Заметим, что метод (2) выгодно отличается простотой реализации и не требует большой машинной памяти. Недостатком метода (2), как и метода ломаных, является необходимость априорного знания константы Lиз условия Липшица.

Метод последовательного перебора, аналогичный методу (2), можно предложить и для некоторых других классов функций. Остановимся на клас­се функций, дважды .дифференцируемых на отрезке, у которых , где- некоторая фиксированная константа. Обозначим этот класс функций через. Заметим, что если, то, и следовательно, монотонно убывает на. Это значит, что тогда функция достигает своей нижней грани пр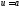и или . Таким образом, задача минимизации функций из классав случаерешается просто. Поэтому имеет смысл рассматривать класс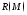при.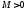

Тогда для решения задачи минимизации первого типа на классе функций можно предложить следующий метод последовательного перебора

(4)

где, ,, а числоопределяется условием.

Теорема4.2.

Применяя метод (3), задачу минимизации первого типа для любой функции можно решить с заданной точностью ,т. е.

(5)

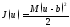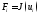В худшем случае (например, если ) может оказаться, что ,, и тогда метод (4) переходит в метод равномерного перебора с шагом . Если же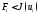 при некоторых (например, для ), то методом (4) удается получить неравенство (5), вообще говоря, при меньшем, чем методом равномерного перебора. Недостатком метода (4) является требование знания константы .