
- •Содержание
- •Введение
- •Глава 1.Численные методы минимизации функций. Минимизация функций одной переменной методом последовательного перебора
- •1.1. Постановка задачи
- •1.2. Локальный минимум и максимум. Унимодальные функции. Связь между задачами максимизации и минимизации.
- •1.3. Метод равномерного перебора. Условие Липшица.
- •Теорема 3.3.
- •Теорема 3.4.
- •1.4. Метод последовательного перебора
- •1.5. Классический метод решения задач минимизации функции одной переменной
- •1.6. Метод половинного деления
- •1.7.Метод парабол
- •1.8. Метод золотого сечения
- •1.9. Применение и особенности численных методов минимизации функций одной переменной
- •Глава 2. Реализация методов равномерного перебора, последовательного перебора.
- •2.1. Реализация методов
- •2.2. Тестирование программы
- •Заключение
- •Список литературы
- •Приложение 1. Текст программы, реализующей метод равномерного перебора.
- •Приложение 2.
Глава 1.Численные методы минимизации функций. Минимизация функций одной переменной методом последовательного перебора
В данной главе представлена общая информация теории минимизации функций одной переменной , а также рассмотрены методы решения задач минимизации — метод равномерного перебора и метод последовательного перебора.
1.1. Постановка задачи
Пусть
задано некоторое множество методов
 ,
класс функций
,
класс функций ,
, —
числовая ось,
—
числовая ось, — некоторое множество из
— некоторое множество из ,
, —функция,
определенная на множестве
—функция,
определенная на множестве и принимающая во всех точках
и принимающая во всех точках конечные значения. Будем рассматривать
задачу минимизации функции
конечные значения. Будем рассматривать
задачу минимизации функции на
множестве
на
множестве .
Начнем с того, что уточним постановку
этой задачи. Для этого сначала напомним
некоторые определения из классического
математического анализа.
.
Начнем с того, что уточним постановку
этой задачи. Для этого сначала напомним
некоторые определения из классического
математического анализа.
Определение 1.1.
Точку
 называютточкой
минимума
функции
называютточкой
минимума
функции
 на множестве
на множестве ,
если
,
если для всех
для всех ;
величину
;
величину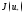 называют
наименьшим или минимальным значением
называют
наименьшим или минимальным значением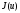 на
на и обозначают
и обозначают .
Множество всех точек минимума
.
Множество всех точек минимума на
на будем обозначать через
будем обозначать через .
.
В
зависимости от свойств множества
 и функции
и функции множество
множество может
содержать одну, несколько или даже
бесконечно много точек, а также возможны
случаи, когда
может
содержать одну, несколько или даже
бесконечно много точек, а также возможны
случаи, когда пусто.
пусто.
Определение 1.2.
Функция
 называетсяограниченной
снизу
на множестве
называетсяограниченной
снизу
на множестве
 ,
если существует такое число
,
если существует такое число ,
что
,
что для
всех
для
всех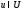 .
Функция
.
Функция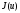 не
ограничена снизу
на
не
ограничена снизу
на
 ,
если существует последовательность
,
если существует последовательность ,
для которой
,
для которой .
.
В
тех случаях, когда
 ,
естественным обобщением понятия
наименьшего значения функции является
понятие нижней грани функции.
,
естественным обобщением понятия
наименьшего значения функции является
понятие нижней грани функции.
Определение 1.3.
Пусть
функция
 ограничена снизу на множестве
ограничена снизу на множестве .
Тогда число
.
Тогда число называютнижней
гранью
называютнижней
гранью на
на
 ,
если: 1)
,
если: 1) при всех
при всех ;
2) для любого сколь угодно малого числа
;
2) для любого сколь угодно малого числа найдется точка
найдется точка ,
для которой
,
для которой .
Если функция
.
Если функция не
ограничена снизу на
не
ограничена снизу на ,
то в качестве нижней грани
,
то в качестве нижней грани на
на принимается
принимается .
Нижнюю грань
.
Нижнюю грань на
на обозначают через
обозначают через .
.
Если ,
то, очевидно, нижняя грань
,
то, очевидно, нижняя грань на
на совпадает
с наименьшим значением этой функции на
совпадает
с наименьшим значением этой функции на ,
т. е.
,
т. е.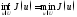 .
В этом случае говорят, что функция
.
В этом случае говорят, что функция на
на достигает своей нижней грани. Подчеркнем,
что
достигает своей нижней грани. Подчеркнем,
что всегда существует, а
всегда существует, а ,
не всегда имеет смысл. Введем еще два
определения.
,
не всегда имеет смысл. Введем еще два
определения.
Определение 1.4.
Последовательность
 называетсяминимизирующей
для функции
называетсяминимизирующей
для функции
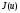 на множестве
на множестве ,
если
,
если .
.
Из определения и существования нижней грани следует, что минимизирующая последовательность всегда существует.
Определение 1.5.
Скажем,
что последовательность
 сходится
к непустому множеству
сходится
к непустому множеству
 ,
если
,
если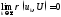 ,
где
,
где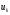
 — расстояние от точки
— расстояние от точки до множества
до множества .
.
Заметим,
что если
 то
всегда существует минимизирующая
последовательность, сходящаяся к
то
всегда существует минимизирующая
последовательность, сходящаяся к ;
например, можно взять стационарную
последовательность
;
например, можно взять стационарную
последовательность ,
где
,
где — какая-либо точка из
— какая-либо точка из .
Однако не следует думать, что при
.
Однако не следует думать, что при любая минимизирующая последовательность
будет сходиться к
любая минимизирующая последовательность
будет сходиться к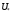 .
.
Определение 1.6.
Пусть
 -погрешность
решения
рассматриваемой задачи минимизации
для функции
-погрешность
решения
рассматриваемой задачи минимизации
для функции
 cпомощью
метода
cпомощью
метода
 .
. -гарантированная
точность метода
-гарантированная
точность метода на классе функции
на классе функции
 .
Метод
.
Метод - оптимальный метод на классе
- оптимальный метод на классе ,
если
,
если ,
а величину
,
а величину -наилучшей
гарантированной точностью методов
-наилучшей
гарантированной точностью методов
 на классе
на классе .
Если для некоторого метода
.
Если для некоторого метода
 выполняется неравенство
выполняется неравенство ,
то
,
то назовем
назовем - оптимальным на классе
- оптимальным на классе .
.
Определение 1.7.
Пусть
 - унимодальная функция на отрезке
- унимодальная функция на отрезке ,
и пусть вычислены значения
,
и пусть вычислены значения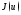 в точках
в точках .Тройка
точек
.Тройка
точек
 локализует минимум функции
локализует минимум функции на отрезке
на отрезке по точкам
по точкам ,
если:
,
если:
точка
 совпадает с одной из точек
совпадает с одной из точек ;
; ;
; ,
причем
,
причем
 - ближайшие к
- ближайшие к точки среди точек
точки среди точек .
.
Определение 1.8.
Пусть
 - класс унимодальных функций на отрезке
- класс унимодальных функций на отрезке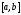 .
На
.
На задан последовательный метод
задан последовательный метод
 ,
если:
,
если:
задано правило выбора первой порции точек
 ,
, ,
по которым определяется тройка точек
,
по которым определяется тройка точек ,
локализующая минимум
,
локализующая минимум
 на
на ;
;при
 на отрезке
на отрезке по заданному правилу выбирается вторая
порция точек
по заданному правилу выбирается вторая
порция точек ,
и по точкам
,
и по точкам определяется тройка
определяется тройка ,
локализующая минимум
,
локализующая минимум на
на ;
;при
 на
отрезке
на
отрезке по
известному правилу выбирается следующая
порция точек
по
известному правилу выбирается следующая
порция точек и по точкам
и по точкам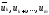 находится
тройка
находится
тройка ,
локализующая минимум
,
локализующая минимум на
на и
т.д. Этот процесс выбора точек отдельными
порциями продолжается до тех пор, пока
не будет выбрана последняя
и
т.д. Этот процесс выбора точек отдельными
порциями продолжается до тех пор, пока
не будет выбрана последняя -я
точка и определена соответствующая
локализующая тройка
-я
точка и определена соответствующая
локализующая тройка .
.
Определение 1.9.
Пусть
 .На
отрезке
.На
отрезке
 задан пассивный метод
задан пассивный метод ,
если задано правило выбора сразу всех
,
если задано правило выбора сразу всех
 точек
точек ,
по которым определяется тройка точек
,
по которым определяется тройка точек ,
локализующая минимум
,
локализующая минимум на
на .
Примером такого метода является метод
равномерного перебора, который будет
рассмотрен немного позднее.
.
Примером такого метода является метод
равномерного перебора, который будет
рассмотрен немного позднее.
