
- •Содержание
- •Введение
- •Глава 1.Численные методы минимизации функций. Минимизация функций одной переменной методом последовательного перебора
- •1.1. Постановка задачи
- •1.2. Локальный минимум и максимум. Унимодальные функции. Связь между задачами максимизации и минимизации.
- •1.3. Метод равномерного перебора. Условие Липшица.
- •Теорема 3.3.
- •Теорема 3.4.
- •1.4. Метод последовательного перебора
- •1.5. Классический метод решения задач минимизации функции одной переменной
- •1.6. Метод половинного деления
- •1.7.Метод парабол
- •1.8. Метод золотого сечения
- •1.9. Применение и особенности численных методов минимизации функций одной переменной
- •Глава 2. Реализация методов равномерного перебора, последовательного перебора.
- •2.1. Реализация методов
- •2.2. Тестирование программы
- •Заключение
- •Список литературы
- •Приложение 1. Текст программы, реализующей метод равномерного перебора.
- •Приложение 2.
1.2. Локальный минимум и максимум. Унимодальные функции. Связь между задачами максимизации и минимизации.
Теперь
можем перейти к формулировке задачи
минимизации функции на множестве
на множестве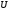 .
В дальнейшем будем различать задачи
двух типов. Кпервому
типу
отнесем задачи, в которых требуется
определить величину
.
В дальнейшем будем различать задачи
двух типов. Кпервому
типу
отнесем задачи, в которых требуется
определить величину
 .
Сразу же подчеркнем, что в задачах
первого типа неважно, будет ли множество
.
Сразу же подчеркнем, что в задачах
первого типа неважно, будет ли множество точек минимума
точек минимума на
на непустым или оно пусто. Ковторому
типу
задач отнесем те задачи, у которых
множество
непустым или оно пусто. Ковторому
типу
задач отнесем те задачи, у которых
множество
 непусто
и требуется наряду с
непусто
и требуется наряду с найти
какую-либо точку
найти
какую-либо точку .
.
Заметим,
что получить точное решение задачи
первого или второго типа удается лишь
в редких случаях. Поэтому на практике
при решении задач первого типа обычно
строят какую-либо минимизирующую
последовательность
 для функции
для функции на
на и затем в качестве приближения для
и затем в качестве приближения для берут
величину
берут
величину при
достаточно большом
при
достаточно большом .
Аналогично для приближенного решения
задач второго типа достаточно построить
минимизирующую последовательность
.
Аналогично для приближенного решения
задач второго типа достаточно построить
минимизирующую последовательность ,
которая сходится ко множеству
,
которая сходится ко множеству в смысле определения 5, и в качестве
приближения для
в смысле определения 5, и в качестве
приближения для и
точки
и
точки взять соответственно величину
взять соответственно величину и
точку
и
точку при
достаточно большом
при
достаточно большом .
.
В
отличие от задач первого типа не всякая
минимизирующая последовательность
может быть использована для получения
приближенного решения задач второго
типа. Построение минимизирующих
последовательностей, сходящихся ко
множеству
 ,
в общем случае требует привлечения
специальных методов. В настоящей работе
будутрассмотрены лишь такие задачи
второго типа, у которых любая минимизирующая
последовательность сходится к
,
в общем случае требует привлечения
специальных методов. В настоящей работе
будутрассмотрены лишь такие задачи
второго типа, у которых любая минимизирующая
последовательность сходится к ,
Один такой класс задач дается следующей
теоремой, называемой теоремой Вейерштрасса.
,
Один такой класс задач дается следующей
теоремой, называемой теоремой Вейерштрасса.
Теорема 2.1. (Вейерштрасса)
Пусть
 — замкнутое ограниченное множество из
— замкнутое ограниченное множество из ,
функция
,
функция непрерывна на
непрерывна на .
Тогда
.
Тогда ограничена
снизу на
ограничена
снизу на ,
множество
,
множество точек минимума
точек минимума на
на непусто,
замкнуто и любая минимизирующая
последовательность
непусто,
замкнуто и любая минимизирующая
последовательность сходится к
сходится к .
.
Возможна и более широкая постановка задач минимизации второго типа — когда ищутся не только точки минимума в смысле определения 1, но и точки так называемого локального минимума.
Определение 2.1.
Точка
 называетсяточкой
локального минимума функции
называетсяточкой
локального минимума функции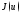 на множестве
на множестве
 со значением
со значением ,
если существует такое число
,
если существует такое число ,
что
,
что для
всех
для
всех .
Если при некотором
.
Если при некотором равенство
равенство для
для возможно
только при
возможно
только при ,
то
,
то называют точкойстрогого
локального минимума.
называют точкойстрогого
локального минимума.
Для
функции, график которой изображен на
рис.2.1, точки
 являются точками строгого локального
минимума, а в точках, удовлетворяющих
неравенствам
являются точками строгого локального
минимума, а в точках, удовлетворяющих
неравенствам и
и ,
реализуется нестрогий локальный минимум.
,
реализуется нестрогий локальный минимум.

рис. 2.1.
Точки
локального минимума, в которых минимум
достигается в смысле определения 1,
часто называют точками
глобального
или абсолютного
минимума функции на множестве
на множестве
 .
.
Выделим класс функций, у которых все точки локального минимума являются точками глобального минимума.
Определение 2.2.
Функцию
 назовемунимодальной
на
отрезке
назовемунимодальной
на
отрезке ,
если она непрерывна на
,
если она непрерывна на и существуют числа
и существуют числа такие, что: 1)
такие, что: 1)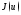 строго монотонно убывает при
строго монотонно убывает при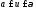 (если
(если );
2)
);
2) строго монотонно возрастает при
строго монотонно возрастает при (если
(если );
3)
);
3) при
при ,
так что
,
так что .
Случаи, когда один пли два из отрезков
.
Случаи, когда один пли два из отрезков ,
, ,
, вырождаются в точку, здесь не исключаются.
В частности, если
вырождаются в точку, здесь не исключаются.
В частности, если ,
то
,
то назовемстрого
унимодальной
на отрезке
назовемстрого
унимодальной
на отрезке
 .
.
Нетрудно
видеть, что если функция
 унимодальна
на
унимодальна
на ,
то она остается унимодальной и на любом
отрезке
,
то она остается унимодальной и на любом
отрезке .
.
В заключение кратко остановимся на задаче максимизации функции.
Определение 2.3.
Функция
 называетсяограниченной
сверху
на множестве
называетсяограниченной
сверху
на множестве
 ,
если существует такое число
,
если существует такое число ,
что
,
что при всех
при всех .
Функция
.
Функция не
ограничена сверхуна
не
ограничена сверхуна
 ,
если существует последовательность
,
если существует последовательность ,
для которой
,
для которой .
Функцию
.
Функцию называютограниченнойна
называютограниченнойна ,
если она ограничена на
,
если она ограничена на сверху и снизу.
сверху и снизу.
Определение 2.4.
Если
функция
 ограничена сверху на
ограничена сверху на ,
то число
,
то число называетсяверхней
гранью
называетсяверхней
гранью на
на в
том случае, когда: 1)
в
том случае, когда: 1) для всех
для всех ;
2) для любого числа
;
2) для любого числа найдется такая точка
найдется такая точка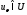 ,
что
,
что .
Если
.
Если не ограничена сверху на
не ограничена сверху на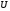 ,
то по определению принимается
,
то по определению принимается .
Последовательность
.
Последовательность называетсямаксимизирующей
для
называетсямаксимизирующей
для
 на
на ,
если
,
если .
Если существует такая точка
.
Если существует такая точка ,
что
,
что ,
то
,
то называетсяточкой
максимума
называетсяточкой
максимума на
на
 ,
а величина
,
а величина —наибольшим
или максимальным
значением
—наибольшим
или максимальным
значением на
на
 .
Множество точек максимума
.
Множество точек максимума на
на будем обозначать через
будем обозначать через ,
верхнюю грань — через
,
верхнюю грань — через .
.
Заметим,
что верхняя грань и максимизирующаяпоследовательность
всегда существуют, а максимальное
значение может не существовать. Если
выполнены условия теоремы 1, то
 ,
и
,
и и
любая максимизирующая последовательность
и
любая максимизирующая последовательность сходится к
сходится к .
.
В
задачах максимизации также можно
различать задачи двух типов: в задачах
первого
типа
ищется величина
 ,
а в задачахвторого
типа
ищется
,
а в задачахвторого
типа
ищется
 и какая-либо точка
и какая-либо точка .
Нетрудно видеть, что
.
Нетрудно видеть, что
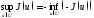 ,
,
причем
любая точка максимума и любая
максимизирующаяпоследовательность
для
 на
на являются
точкой минимума и соответственно
минимизирующей последовательностью
для функции —
являются
точкой минимума и соответственно
минимизирующей последовательностью
для функции — на
на .
Это значит, что любая задача максимизации
функции
.
Это значит, что любая задача максимизации
функции на
на равносильна
задаче минимизации функции —
равносильна
задаче минимизации функции — на том же множестве
на том же множестве .
Поэтому мы можем ограничиться изучением
лишь задач минимизации.
.
Поэтому мы можем ограничиться изучением
лишь задач минимизации.
Наконец, немного о точках локального максимума.
Определение 2.5.
Точка
 называетсяточкой
локального максимума
функции
называетсяточкой
локального максимума
функции
 на множестве
на множестве ,
если существует такое число
,
если существует такое число ,
что
,
что для всех
для всех .
Если при некотором
.
Если при некотором равенство
равенство для
для возможно
только при
возможно
только при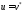 ,то
,то называютточкой
строгого локального максимума.
называютточкой
строгого локального максимума.
Для
функции, график которой изображен на
рис., точки
 являются точками строгого локального
максимума, а в точках, удовлетворяющих
неравенствам
являются точками строгого локального
максимума, а в точках, удовлетворяющих
неравенствам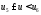 и
и ,
реализуется нестрогий локальный
максимум;
,
реализуется нестрогий локальный
максимум; —точка
глобального максимума.
—точка
глобального максимума.
Множество
всех точек локального минимума и
максимума функции на множестве
 принято называтьточками
локального экстремума
функции на этом множестве или, проще,
точками
экстремума.
принято называтьточками
локального экстремума
функции на этом множестве или, проще,
точками
экстремума.
