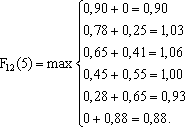3.3. Теоремы Куна—Таккера

В предыдущем разделе построены условия Куна—Таккера для задач условной оптимизации. С помощью метода множителей Лагранжа получено интуитивное представление о том, что условия Куна — Танкера тесно связаны с необходимыми условиями опти­мальности. В данном разделе рассматриваются строгие формули­ровки необходимых и достаточных условий оптимальности решения задачи нелинейного программирования.

Теорема 1. Необходимость условий Куна—Таккера

Рассмотрим задачу нелинейного программирования (0)-(2). Пусть -  дифференцируемые функции, а х* — допус­тимое решение данной задачи. Положим. Далее пустьлинейно неза­висимы. Если х* — оптимальное решение задачи нелинейного про­граммирования, то существует такая пара векторов, чтоявляется решением задачи Куна—Таккера (3)—(7).

Условие, согласно которому должны быть линейно независимыми, известно как ус­ловие линейной независимости и по существу представляет собой некоторое условие регулярности допустимой области, которое поч­ти всегда выполняется для встречающихся на практике задач опти­мизации. Однако вообще проверка выполнения условия линейной независимости весьма затруднительна, так как требуется, чтобы оптимальное решение задачи было известно заранее. Вместе с тем условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свой­ствами.

1. Все ограничения в  виде равенств и  неравенств содержат линейные функции.

2. Все ограничения в виде неравенств содержат вогнутые функ­ции,  все ограничения-равенства — линейные функции, а также существует, по крайней мере, одна допустимая точка х, которая рас­положена во внутренней части области,  определяемой ограниче­ниями-неравенствами. Другими словами, существует такая точка х, что

Если условие линейной независимости в точке оптимума не вы­полняется, то задача Куна—Таккера может не иметь решения.

Пример 4

Минимизировать 

при ограничениях 

Решение.

На рис.1 изображена область допустимых ре­шений сформулированной выше нелинейной задачи. Ясно, что оптимальное решение этой задачи есть . Пока­жем, что условие линейной независимости не выполняется в точке оптимума.

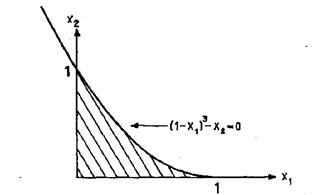
Рис.1 Допустимая область в задаче 4

Так как

Легко видеть, что векторы линейно зависимы, т. е. условие линейной независимости в точкене выпол­няется.

Запишем условия Куна—Таккера и проверим, выполняются ли они в точке (1, 0). Условия (3), (6) и (7) принимают сле­дующий вид;

(11)

(12)

(13)

(14)

(15)

(16)

При из уравнения (11) следует, что, тогда как уравнение (14) дает, Следовательно, точка оптимума не является точкой Куна — Таккера. Заметим, что нарушение условия линейной независимости не обязательно означает, что точка Куна—Таккера не существует. Для того чтобы подтвердить это, заменим целевую функцию из этого примера функцией. При этом оптимум по-прежнему достигается в точке (1,0), в которой условие линейной независимости не выполняется. Условия Куна—Так­кера (12) - (16) остаются неизменными, а уравнение (11) принимает вид

Нетрудно проверить, что точка является точкой Куна—Таккера, т. е. удовлетворяет условиям Куна—Таккера.

Теорема о необходимости условий Куна—Таккера позволяет идентифицировать неоптимальные точки. Другими словами, тео­рему 1 можно использовать для доказательства того, что задан­ная допустимая точка, удовлетворяющая условию линейной неза­висимости, не является оптимальной, если она не удовлетворяет условиям Куна—Таккера. С другой стороны, если в этой точке условия Куна—Таккера выполняются, то нет гарантии, что най­дено оптимальное решение нелинейной задачи. В качестве примера рассмотрим следующую задачу нелинейного программирования.

Следующая теорема устанавливает условия, при выполнении которых точка Куна—Таккера автоматически соответствует оптимальному решению задачи нелинейного программирования.

Теорема.2 Достаточность условий Куна—Таккера

Рассмотрим задачу нелинейного программирования (0) — (2). Пусть целевая функция выпуклая, все ограничения в виде неравенств содержат вогнутые функции, а ограничения в виде равенств содержат линейные функции. Тогда если существует решение, удовлет­воряющее условиям Куна—Таккера (3) — (7), то х* — оп­тимальное решение задачи нелинейного программирования.

Если условия теоремы 2 выполняются, то нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования.

Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример:

Минимизировать 

при ограничениях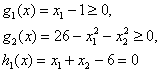 

С помощью теоремы 2 докажем, что решение является оптимальным. Имеем

Так как матрица положительно полуопределена при всех х, функцияоказывается выпуклой. Первое ограничение в виде неравенства содержит линейную функцию, которая одновре­менно является как выпуклой, так и вогнутой. Для того

чтобы показать, что функция является вогнутой, вычислим

Поскольку матрица отрицательно определена, функцияявляется вогнутой. Функциявходит в линейное ограни­чение в вяде равенства. Следовательно, все условия теоремы 2 выполнены; если мы покажем, что- точка Куна-Так­кера, то действительно установим оптимальность решения. Условия Куна-Таккера для примера 2 имеют вид

(22)

(23)

(24)

(25)

,  (26)

, (27)

(28)

(29)

Точка удовлетворяет ограничениям (24) — (26) и, следовательно, является допустимой. Уравнения (22) и (23) принимают следующий вид:

Положив ,получими. Таким образом, реше­ние х*=(1, 5),удовлетворяет условиям Куна—Таккера. Поскольку условия теоремы 2 выполнены, тооптимальное решение задачи из примера 3. Заметим, что существуют также и другие значенияи, которые удов­летворяют системе (22) -(29).

Замечания

1.Для  встречающихся на практике задач условие линейной независимости,   как   правило,   выполняется.   Если   в  задаче   все функции  дифференцируемы,  то точку   Куна—Таккера  следует рассматривать как возможную точку оптимума. Таким образом, многие из методов нелинейного программирования сходятся к точке Куна—Таккера. (Здесь уместно провести аналогию со случаем безусловной оптимизации, когда соответствующие алгоритмы позволяют определить стационарную точку.)

2. Если условия теоремы 2 выполнены, точка Куна—Таккера в то же время оказывается точкой глобального минимума. К сожа­лению, проверка достаточных условий весьма затруднительна, и, кроме того, прикладные задачи  часто не обладают требуемыми свойствами. Следует отметить, что наличие хотя бы одного нелиней­ного ограничения в виде равенства приводит к нарушению предпо­ложений теоремы 2.

3.Достаточные условия, установленные теоремой 2, можно обобщить на случай задач с невыпуклыми функциями, входящими в ограничения в виде неравенств, невыпуклыми целевыми функ­циями и нелинейными ограничениями-равенствами. При этом ис­пользуются такие обобщения выпуклых функций, как квазивыпук­лые и псевдовыпуклые функции.

21. Вариационное исчисление

Вариацио́нное исчисле́ние — это раздел функционального анализа, в котором изучаютсявариациифункционалов. Самая типичная задача вариационного исчисления состоит в том, чтобы найтифункцию, на которойфункционалдостигаетэкстремальногозначения. Методы вариационного исчисления широко применяются в различных областяхматематики, вдифференциальной геометриис их помощью ищутгеодезическиеиминимальные поверхности. В физике вариационный метод — одно из мощнейших орудий получения уравнений движения (см. напримерПринцип наименьшего действия), как для дискретных, так и для распределённых систем, в том числе и для физических полей. Методы вариационного исчисления применимы и в статике (см.Вариационные принципы).Важнейшими понятиями вариационного исчисления являются следующие: 1. вариация (первая вариация), 2. вариационная производная (первая вариационная производная), 3. кроме первой вариации и первой вариационной производной, рассматриваются и вариации и вариационные производные второго и высших порядков.

Вариация

Аналогом дифференциала (первого дифференциала) является в вариационном исчислении вариация (первая вариация):

(как и в случае дифференциала имеется в виду линейная часть этого приращения, а выражаясь традиционным образом — выбирается бесконечно малой, и при вычислении разности отбрасываются бесконечно малые высших порядков). При этом— играющее роль дифференциала или малого приращения независимой переменной — называется вариацией.

Как видим, сама в свою очередь является функционалом, так как она, вообще говоря, различна для разных(также и для разных).

Таким образом, это — в применении к функционалам — прямой аналог дифференциала функции конечномерного (в том числе одномерного) аргумента:

— точно так же понимаемого как линейная часть приращения функции при бесконечно малом приращении аргумента(или линейный член при разложениипо степенямвблизи точки).

Производная по направлению

(Производная Гато) Производной функционалав точкепо направлению, очевидно, будет

Этого в принципе уже достаточно для решения типичной вариационной задачи — нахождения «стационарных точек», то есть таких функций , для которых первая вариация или производная по направлению обращается в ноль для любой бесконечно малойили любой конечной. Именно эти «точки» в пространстве функций — то есть именно такие функции — являются кандидатами в экстремали (проверку того, действительно ли они являются экстремалями, то есть достигается ли на них локальный экстремум, надо делать отдельно, как и в случае функций конечномерного аргумента; интересно, что во многих задачах физики важнее найти не экстремали, а именно стационарные точки).

Вариационная производная

Для интегральных функционалов, которые являются очень важным для математики и приложений случаем, можно ввести не только аналог дифференциала и производную по направлению, но ипроизводную Фреше— аналог конечномерногоградиента, называемую вариационной производной.

То есть, в полной аналогии с конечномерным случаем, когда

, где — обозначение градиента (или производной Фреше) функции, а— скалярное произведение;— оператор частной производной по-той координате, сумма представляет собойполный дифференциал.

Для функционала имеем

, где — обозначение вариационной производной, а суммирование конечномерной формулы естественно заменено интегрированием.

Итак, — стандартное обозначение вариационной производной. Это также некая функция как от, так и(вообще говоря, этообобщённая функция, но эта оговорка выходит за рамки рассмотрения, так как предполагается, что все функции и функционалы сколь угодно гладки и не имеют особенностей).

Иными словами, если можно представить вариацию

в виде

, где — некоторая функция, тоесть вариационная производнаяпо(«по» здесь означает, что остальные аргументы или параметры не меняются; речевой оборот «по» можно опустить в случае, когда точно определено, функционалом от какой функции рассматривается, что на практике может быть не ясным из самой его формулы, в которую могут входить и другие параметры и функции — см. также ниже).То есть

Легко видеть, что это определение обобщается на любую размерность интеграла. Для -мерного случая верна прямо обобщающая одномерный случай формула:

Так же легко обобщается понятие вариационной производной на случай функционалов от нескольких аргументов[4]:

Вариации и вариационные производные второго и высших порядков

Как это описано выше для первого порядка, можно ввести понятие второй вариации и второй вариационной производной функционала, а также -ой вариации и-ой вариационной производной:

Для функционалов, зависящих от нескольких функций, можно также ввести понятие смешанных вариационных производных разного порядка, например:

Здесь мы не будем останавливаться на этом подробно, всё делается полностью аналогично введению соответствующих дифференциалов и производных для функции конечномерного аргумента.

Функционал вблизи конкретной точки в пространстве функций раскладывается в ряд Тейлора, если, конечно, вариационные производные всех порядков существуют. Как и в конечномерных случаях, сумма конечного числа членов этого ряда даёт значение функционала с определённой точностью (соответствующего порядка малости) лишь при небольших отклонениях его аргумента (при бесконечно малых). Кроме того, как и в случае функций конечномерного аргумента, ряд Тейлора (сумма всех членов) может не сходиться к функционалу, в него разложенному, при любых ненулевых конечных смещениях, хотя такие случаи достаточно редки в приложениях.

Применение вариационного исчисления

Хотя задачи, к которым применимо вариационное исчисление, заметно шире, в приложениях они главным образом сводятся к двум основным задачам:

нахождение точекв пространстве функций, на котором определён функционал — точек стационарного функционала, стационарных функций, линий, траекторий, поверхностей и т. п., то есть нахождение для заданноготаких, для которыхпри любом (бесконечно малом), или, иначе, где, нахождение локальных экстремумов функционала, то есть в первую очередь определение тех, на которыхпринимает локально экстремальные значения  нахождение экстремалей (иногда также определение знака экстремума).

Очевидно, обе задачи тесно связаны, и решение второй сводится (при должной гладкости функционала) к решению первой, а затем проверке, действительно ли достигается локальный экстремум (что делается независимо вручную, или — более систематически — исследованием вариационных производных второго и, если все они одного знака и хотя бы одна из них равна нулю, то и более высокого порядка). В описанном процессе выясняется и тип экстремума. Нередко (например, когда функция стационарного функционала единственная, а все изменения функционала при любом большом возмущении имеют один и тот же знак) решение вопроса, экстремум ли это и какого он типа, заранее очевидно.

При этом очень часто задача (1) оказывается не менее или даже более важной, чем задача (2), даже когда классификация стационарной точки неопределённа (то есть она может оказаться минимумом, максимумом или седловой точкой, а также слабым экстремумом, точкой, вблизи которой функционал точно постоянен или отличается от постоянного в более высоком порядке, чем второй). Например, в механике (и вообще в физике) кривая или поверхность стационарной потенциальной энергии означает равновесие, а вопрос, является ли она экстремалью, связан лишь с вопросом об устойчивости этого равновесия (который далеко не всегда важен). Траектории стационарного действияотвечают возможному движению, независимо от того, минимально действие на такой траектории, максимально, или седловидно. То же можно сказать о геометрической оптике, где любая линия стационарного времени (а не только минимального, как в простой формулировкепринципа наименьшего времени Ферма) соответствует возможному движению светового луча неоднородной оптической среде. Есть системы, где вообще нет экстремалей, но стационарные точки существуют.

22. Динамическое программирование

Краткие теоретические сведения

Динамическое программирование представляет собой математический аппарат, позволяющий осуществлять оптимальное планирование управляемых процессов, то есть процессов, на ход которых можно целенаправленно влиять. Это метод оптимизации, специально приспособленный к операциям, в которых процесс принятия решений может быть разбит на отдельные шаги. Такие операции называют многошаговыми. Задача динамического программирования состоит в выборе из мно­жества допустимых управлений (решений) такого, которое переводит систему из начального состояния в конечное, обеспечивая при этом экстремум целевой функции (минимум или максимум в зависимости от ее экономической сущности). В основе вычислительных алгоритмов динамического программирования лежит следующий принцип оптимальности, сформулированный Р. Беллманом: каково бы ни было состояние системы S в результате (i‑1) шагов, управление на i-м шаге должно выбираться так, чтобы оно по совокупности с управлениями на всех последующих шагах с (i+1)‑го до N‑го включительно доставляло экстремум целевой функции. Динамическое программирование используется для исследования многоэтапных процессов. Состояние управляемой системы характеризуется определенным набором параметров. Процесс перемещения в пространстве разделяют на ряд последовательных этапов и производят последовательную оптимизацию каждого из них, начиная с последнего. На каждом этапе находят условное оптимальное управление при всевозможных предположениях о результатах предыдущего шага. Когда процесс доходит до исходного состояния, снова проходят все этапы, но уже из множества условных оптимальных управлений выбирается одно наилучшее. Получается, что однократное решение сложной задачи заменяется многократным решением простой. Важно, что значение критерия – сумма частных значений, достигнутых на отдельных шагах, и предыстория не играют роли при определении будущих действий.

Контрольный пример

Пусть фирма имеет три торговые точки, какое-то количество условных единиц капитала и знает для каждой точки зависимость прибыли в ней от объема вложения определенного капитала в эту точку (табл. 6.1).  Таблица 6.1 Вложения 1 2 3 0 0 0 0 1 0,28 0,25 0,15 2 0,45 0,41 0,25 3 0,65 0,55 0,40 4 0,78 0,65 0,50 5 0,90 0,75 0,62 6 1,02 0,80 0,73 7 1,13 0,85 0,82 8 1,23 0,88 0,90 9 1,32 0,90 0,96 Определить, как распорядиться имеющимся капиталом, чтобы прибыль была максимальна? Введем следующие обозначения: f1(x), f2(x), f3(х) – функции прибыли в зависимости от капитальных вложений, то есть столбцы 2–4 таблицы, F12(А) – оптимальное распределение, когда A единиц капитала вкладывается в первую и вторую торговые точки вместе, F123{А) – оптимальное распределение капитала величины A, вкладываемого во все точки вместе. Например, для определения F12(2) надо найти f1(0)+f2(2)=0,41, f1(1)+f2(1)=0,53 f1(2)+f2(0)=0,45 и выбрать из них максимальную величину, то есть F12(2)=0,53. Вообще F12(A)=max [f1(x)–f2(A-x)]. Вычисляем F12(0), F12(1), F12(2), …, F12(9). Распределение капитала между двумя торговыми точками (табл. 6.2). Таблица 6.2 Вложения f1(x) f2(x) F12(A) Оптимальное распределение 0 0 0 0 0,0 1 0,28 0,25 0,28 1,0 2 0,45 0,41 0,53 1,1 3 0,65 0,55 0,70 2,1 4 0,78 0,65 0,90 3,1 5 0,90 0,75 1,06 3,2 6 1,02 0,80 1,20 3,3 7 1,13 0,85 1,33 4,3 8 1,23 0,88 1,45 5,3 9 1,32 0,90 1,57 6,3  Для А=4 возможны комбинации (4, 0), (3, 1), (2, 2), (1, 3), (0, 4), ко­торые дают соответственно общую прибыль: 0,78; 0,90; 0,86; 0,83; 0,65. Более подробно получение этих величин показано ниже: , Теперь, когда фактически есть зависимость F12 от величины вкладываемого в первые две точки капитала, можно искать F123(A)=max [F12(x)+f3(A-x)] (табл. 6.3). Таблица 6.3 Вложения F12(х) f3(x) F123(A) Оптимальное распределение 0 0 0 0 (0,0,0) 1 0,28 0,15 0,28 (1,0,0) 2 0,53 0,25 0,53 (1,1,0) 3 0,70 0,40 0,70 (2,1,0) 4 0,90 0,50 0,90 (3,1,0) 5 1,06 0,62 1,06 (3,2,0) 6 1,20 0,73 1,21 (3,2,1) 7 1,33 0,82 1,35 (3,3,1) 8 1,45 0,90 1,48. (4,3,1) 9 1,57 0,96 1,60 (5,3,1) или (3,3,3) Более подробно получение этих величин при вложении капитала в три точки показано в табл. 6.4 для девяти единиц капитала. Таблица 6.4 Капитал х1+х2 х3 F123 9 9 0 1,57   8 1 1,45 + 0,15 = 1,6 (5,3,1)   7 2 1,33 + 0,25 = 1,58   6 3 1,2 + 0,4 = 1,6 (3,3,3)   5 4 1,06 + 0,5 = 1,56   4 5 0,9 + 0,62 = 1,52   3 6 0,70 + 0,73 = 1,43   2 7 0,53 + 0,82 = 1,35   1 8 0,28 + 0,90 = 1,18   0 9 0,96 Важно то, что полученные результаты были бы теми же, если бы использовались не F12 и F123, а, скажем, F31 и F312. Обратите внимание на то, что оптимальное решение для А=9 не единственное.

23. Теорема Байеса

Теорема Байеса имеет дело с расчетом вероятности верности гипотезы в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях. Другими словами, по формуле Байеса можно более точно пересчитывать вероятность, беря в учет как ранее известную информацию, так и данные новых наблюдений. Главная, видимо, особенность теоремы Байеса в том, что для ее практического применения обычно требуется огромное количество вычислений-пересчетов, а потому расцвет методов байесовых оценок пришелся аккурат на революцию в компьютерных и сетевых инфотехнологиях.  Пример, из 20 студентов, пришедших на экзамен, 8 подготовлены отлично, 6 - хорошо, 4 - посредственно и 2 - плохо.  В экзаменнационных билетах всего 40 вопросов.  Студент подготовленный отлично, знает все вопросы, хорошо - 35, посредственно - 25 и плохо - 10 вопросов.  Некий студент ответил на все билеты. Какова вероятность того, что он подготовлен плохо? Гипотезы прихода на экзамен отличника (8/20), хорошиста (6/20), троечника (4/20), двоечника (2/20). Есть вероятность того, что среди вопросов билета студент выпадет знакомый (40/40, 35/40, 25/40, 10/40 соответсвенно). Вероятность что хорошо ответил отличник Ротл=(8/20)*1=2/5; хорошист - Рхор=(6/20)*(35/40)=21/80; троечник - Ртро=(4/20)*(25/40)=1/8; и, наконец, двоечник - Рдво=(2/20)*(10/40)=1/40.  Применяя теорему Байеса, вычисляем вероятность того, что ответивший студент был двоечником Р[сдал/двоечник]=Рдво/(Рдво+Ртро+Рхор+Ротл)=(1/40)/(1/40+1/8+21/80+2/5)=2/65 

24. Метод парных сравнений

Метод предусматривает использование эксперта, который проводит оценку целей. Z1, Z2, ...,Zn.

Согласно методу осуществляются парные сравнения целей во всех возможных сочетаниях. В каждой паре выделяется наиболее предпочтительная цель. И это предпочтение выражается с помощью оценки по какой-либо шкале. Обработка матрицы оценок позволяет найти веса целей, характеризующие их относительную важность. Одна из возможных модификаций метода состоит в следующем:

составляется матрица бинарных предпочтений, в которой предпочтение целей выражается с помощью булевых переменных;

определяется цена каждой цели путем суммирования булевых переменных по соответствующей строке матрицы.

Примеp1:

эксперт проводит оценку 4-х целей, которые связаны с решением транспортной проблемы.

Z1 — построить метрополитен

Z2 — приобрести 2-хэтажный автобус

Z3 — расширить транспортную сеть

Z4 — ввести скоростной трамвай

Составим матрицу бинарных предпочтений:

Zi / Zj	Z1	Z2	Z3	Z4
Z1		1	1	1
Z2	0		0	0
Z3	0	1		1
Z4	0	1	0

Определим цену каждой цели (складываем по строкам)

C1=3; C2=0; C3=2; C4=1

Эти числа уже характеризуют важность объектов. Нормируем, т.к. этими числами не удобно пользоваться.

Исковые веса целей.

V1=3/6=0,5 ; V2=0; V3=0,17

Проверка:

Получаем следовательно порядок предпочтения целей:

Z1, Z3, Z4, Z2

Примеp2:

cумма всех Vi=1, значит решено верно.

Белорусские авиалинии «Белавиа» получили возможность приобрести самолет Боинг 747 — встал вопрос об открытии нового чартерного рейса. Были предложены направления:

Лондон

Пекин

Сеул

Владивосток

Тель-Авив

Zi / Zj	Z1	Z2	Z3	Z4	Z5
Z1		1	1	1	1
Z2	0		0	0	0
Z3	0	1		1	1
Z4	0	1	0		1
Z5	0	1	0	0

Где Z1...j — направления

Определить наиболее выгодный рейс.

Решение:

void main(void)

{

//Введем исходную матрицу бинарных предпочтений

for(i=1;i<5;i++) Predpochtenia[0][i]=1;

Predpochtenia[1][0]=0;

for(i=2;i<5;i++) Predpochtenia[1][i]=0;

Predpochtenia[2][0]=0;

Predpochtenia[2][1]=1;

......

//Определим цену каждой цели

int c[5];

for(i=0;i<5;i++) c[i]=0;

for(i=0;i<5;i++)

{

for(j=0;j<5;j++)

{

if(i!=j)

{

c[i]+=Predpochtenia[i][j];

}

}

}

//Определяем веса целей

int sum=0;

for(i=0;i<5;i++)

{

sum+=c[i];

}

double v[5][2];

for(i=0;i<5;i++)

{

v[i][0]=double(c[i])/double(sum);

v[i][1]=i+1;

}

//Далее надо отсортировать цели по возрастанию

for(i=0;i<5;i++)

{

for(j=1;j<5;j++)

if(v[i][0] < v[j][0] && i {

........

}

}

Результат:

0,4 0 0,3 0,2 0,1

1 3 4 5 2

Вывод: Наиболее выгодный рейс — рейс номер 1, т.к. искомый вес целей самый большой: 0,4.

25. Многоцелевые модели принятия решений. Метод анализа иерархий.

Многоцелевые модели. В этих моделях каждая альтернатива оценивается множеством критериев, поэтому они называются также многокритериальными. К наиболее известным многокритериальным моделям относятся многомерные функции полезности, модели многомерного шкалирования, метод анализа иерархий (метод собственных значений).

Из многомерных моделей наиболее часто используются аддитивные и мультипликативные многомерные функции полезности. Функцией полезности (ценности) называется скалярная функция U, устанавливающая отношение порядка на множестве вариантов

U(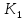,...,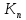)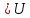(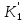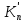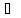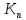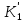,...,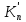)(,...,)(,...,), (5.2.5)

где – символ “более предпочтителен, чем”; (,...,) – точка пространства последствий (критериального пространства). Обобщенная форма аддитивной модели полезности имеет вид

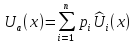, (5.2.6)

где 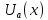– функция полезности варианта x;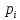– вес фактора (критерия)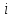;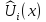– оценка полезности варианта x по критерию.

Обобщенная форма мультипликативной функции полезности имеет вид

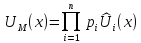. (5.2.7)

Оценки 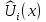, как правило, получаются экспертным путем, но могут задаваться и аналитически применением подходящей аппроксимирующей функции. Аддитивная функция слабо чувствительна к изменению свойств с малыми весами (малыми оценками полезности); мультипликативная, наоборот, сильно зависит от изменения свойств с малыми значениями оценок полезности. В теории принятия решений доказывается, что функция полезности имеет аддитивный вид, если факторы, входящие в модель, аддитивно независимы. Функция полезности имеет мультипликативную форму, если факторы взаимно независимы по полезности. Первое требование означает фактически уверенность эксперта в том, что модель является линейной по факторам, а второе – что модель содержит взаимодействия факторов различных порядков. На практике обычно веса pi нормализуют так, что обе формы представления

оказываются эквивалентными (могут быть преобразованы друг в друга). Многомерные модели сравнения вариантов различаются подходами к установлению весов факторов и подфакторов и схемами их агрегирования. Стандартная процедура сравнения вариантов по многим факторам включает

формулирование задачи, выбор факторов и подфакторов, построение дерева решений, назначение весов факторам и их нормализацию, назначение весов подфакторам и нормализацию весов, подсчет показателей (баллов) по всем факторам для каждого варианта, получение взвешенных оценок и суммарного числового выражения полезности для каждого варианта решения. Основные неформальные шаги в этом алгоритме – выбор факторов и подфакторов, построение дерева решений и назначение весов факторам и подфакторам.

Метод Анализа Иерархий (МАИ) — математический инструмент системного подхода к сложным проблемам принятия решений. МАИ не предписывает лицу, принимающему решение (ЛПР), какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант (альтернативу), который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению. Этот метод разработан американским математиком Томасом Саати, который написал о нем книги, разработал программные продукты и в течение 20 лет проводит симпозиумы ISAHP (англ.International Symposium on Analytic Hierarchy Process). МАИ широко используется на практике и активно развивается учеными всего мира. В его основе наряду сматематикойзаложены ипсихологическиеаспекты. МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, сравнить и выполнить количественную оценку альтернативных вариантов решения. Метод Анализа Иерархий используется во всем мире для принятия решений в разнообразных ситуациях: от управления на межгосударственном уровне до решения отраслевых и частных проблем вбизнесе,промышленности,здравоохранениииобразовании. Для компьютерной поддержки МАИ существуют программные продукты, разработанные различными компаниями. Анализ проблемы принятия решений в МАИ начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор. Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты как материальные, так и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки[1]. Иными словами, анализ ситуации выбора решения в МАИ напоминает процедуры и методы аргументации, которые используются на интуитивном уровне. Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ. На заключительном этапе анализа выполняется синтез (линейная свертка) приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета.

Метод анализа иерархий содержит процедуру синтеза приоритетов, вычисляемых на основе субъективных суждений экспертов. Число суждений может измеряться дюжинами или даже сотнями. Математические вычисления для задач небольшой размерности можно выполнить вручную или с помощью калькулятора, однако гораздо удобнее использовать программное обеспечение(ПО) для ввода и обработки суждений. Самый простой способ компьютерной поддержки — электронные таблицы, самое развитое ПО предусматривает применение специальных устройств для ввода суждений участниками процесса коллективного выбора. Порядок применения Метода Анализа Иерархий:

• Построение качественной модели проблемы в виде иерархии, включающей цель, альтернативные варианты достижения цели и критерии для оценки качества альтернатив.

• Определение приоритетов всех элементов иерархии с использованием метода парных сравнений.

• Синтез глобальных приоритетов альтернатив путем линейной свертки приоритетов элементов на иерархии.

• Проверка суждений на согласованность.

• Принятие решения на основе полученных результатов. 

J = (#Jf#)/(#S#),

где #Jf# – число разнотипных по функциям систем; #S# – общее число подсистем. Основные этапы процесса структурного моделирования

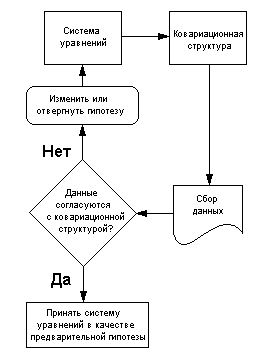
26. Принятие решений методом «Дерево решений»

Деревья решений – это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение. Под правилом понимается логическая конструкция, представленная в виде "если ... то ...". 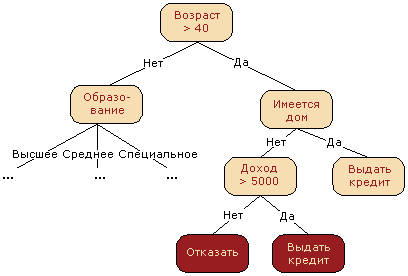Область применения деревья решений в настоящее время широка, но все задачи, решаемые этим аппаратом могут быть объединены в следующие три класса:

• Описание данных: Деревья решений позволяют хранить информацию о данных в компактной форме, вместо них мы можем хранить дерево решений, которое содержит точное описание объектов. 

• Классификация: Деревья решений отлично справляются с задачами классификации, т.е. отнесения объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные значения.

• Регрессия: Если целевая переменная имеет непрерывные значения, деревья решений позволяют установить зависимость целевой переменной от независимых(входных) переменных. Например, к этому классу относятся задачи численного прогнозирования(предсказания значений целевой переменной).

 Другое определение: деревья решений - это способ представления правил в иерархической, последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение. Деревья решений разбивают данные на группы на основе значений переменных, в результате чего возникает иерархия операторов "ЕСЛИ - ТО", которые классифицируют данные.

Под правилом понимается логическая конструкция вида «если - то».

• Объект – некоторый пример, действие, шаблон, наблюдение.

• Атрибут – признак, свойство.

• Узел – внутренний узел дерева, узел проверки.

• Лист – конечный узел дерева, узел решения.

2 Построение деревьев Способ 1.

Рисуют деревья слева направо. Места, где принимаются решения, обозначают квадратами, места появления исходов – кругами, возможные решения – пунктирными линиями, возможные исходы – сплошными линиями. Для каждой альтернативы мы считаем ожидаемую стоимостную оценку (EMV) – максимальную из сумм оценок выигрышей, умноженных на вероятность реализации выигрышей, для всех возможных вариантов (см. пример 1).

Пример 1. Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий: а). Построить большой завод стоимостью Ст1 = 500 тысяч у.е. При этом варианте возможны большой спрос (годовой доход в размере Д1 = 200 тысяч у.е. в течение следующих 5 лет) с вероятностью p1 = 0,7 и низкий спрос (ежегодные убытки Д2 = 90 тысяч у.е.) с вероятностью р2 = 0,3. б). Построить маленький завод стоимостью Ст2 = 300 тысяч у.е. При этом варианте возможны большой спрос (годовой доход в размере Д3 = 100 тысяч у.е. в течение следующих 5 лет) с вероятностью p3 = 0,7 и низкий спрос (ежегодные убытки Д4 = 40 тысяч у.е.) с вероятностью р4 = 0,3. в). Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью p5 = 0,4 и p6 = 0,6 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на p7 = 0,8 и р8 = 0,2 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет. Нарисовав дерево решений, определим наиболее эффективную последовательность действий, основываясь на ожидаемых доходах. Решение. Строим дерево решений. Строим узел 1, из которого исходят три заявленные в условии варианты. Обозначаем эти ветви пунктиром, поскольку это – возможные решения. На концах ветвей ставим узлы-исходы, заключаем их в круг и обозначаем буквами А, В и т.д. Рисуем из этих узлов-исходов ветви с возможными исходами при выборе того или иного варианта из условия. Под каждой ветвью подписываем вероятности соответствующих исходов. На концах каждой ветви, не закрытой новым узлом, выставляем доходы и убытки, умноженные (исходя из условия) на время (годы из условия). На ветвях (возможные решения) ставим стоимость строительства со знаком «-», так как это расходы компании. Убытки на концах «открытых» ветвей также пишем со знаком «-». Рис.1 – Дерево решений для примера 1. Первый этап построения Далее считаем ожидаемые стоимостные оценки узлов. Ожидаемая стоимостная оценка узла А равна: ЕМV(А) = 0,8 х 1000 + 0,2 х (-450) -500 = 210. EMV( B) = 0,8 х 500 + 0,2 х (-200) - 300 = 60. EMV( D) = 0,9 x 800 + 0,1 x (-360) - 500 = 184. EMV(E) = 0,9 x 400 + 0,1 х (-160) - 300 = 44. Для узлов принятия решения 2 (второй уровень, условно) выбираем максимальную оценку: EMV(2) = max {EMV( D), EMV( E)} = max {184, 44} = 184 = EMV(D). Поэтому в узле 2 отбрасываем возможное решение «маленький завод». EMV(C) = 0,7 x 184 + 0,3 x 0 = 128,8. Для узла принятия решения 1 – узла принятия окончательного решения, аналогично выбираем максимальную оценку на других узлах. EMV(1) = max {ЕМV(A), EMV(B), EMV(C)} = max {210; 60; 128,8} = 210 = EMV(А). Поэтому в узле 1 выбираем решение «большой завод». Исследование проводить не нужно. Строим большой завод. Ожидаемая стоимостная оценка этого наилучшего решения равна 210 тысяч у.е. Ответ: наиболее подходящее решение – решение строить большой завод. Рис.2 – Дерево решений со стоимостными оценками В рассмотренном примере мы произвели отсечение ветвей в узле 2. И далее в задаче мы отсекаем те ветви и узлы, стоимостные оценки которых не приемлемы для принятия наиболее выгодного решения.