12.3. Системы управления базами данных

Система управления базами данных (СУБД) – это программное обеспечение, с помощью которого пользователи могут определять, создавать и поддерживать базу данных, а также осуществлять к ней контролируемый доступ.

Различают 2 класса СУБД:

1) системы общего назначения;

2) специализированные системы.

Системы СУБД общего назначения не ориентированы на какую-либо конкретную предметную область или на информационные потребности конкретной группы пользователей. Реализуются как программный продукт, способный функционировать на некоторой модели ЭВМ в определенной операционной системе. Использование СУБД общего назначения в качестве инструментального средства для создания информационных систем, основанных на технологии баз данных, позволяет существенно сокращать сроки разработки и экономить трудовые ресурсы.

В процессе реализации своих функций СУБД постоянно взаимодействует с базой данных и с другими прикладными программными продуктами пользователя.

Современные СУБД имеют следующие возможности:

1) включают язык определения данных, с помощью которого можно определить базу данных, ее структуру, типы данных, а также средства задания ограничения для хранимой информации;

2) позволяют вставлять, удалять, обновлять и извлекать информацию из базы данных посредством языка запросов (SQL);

3) большинство СУБД могут работать на компьютерах с разной архитектурой и под разными операционными системами;

4) многопользовательские СУБД имеют развитые средства администрирования баз данных.

В работе с СУБД возможны следующие режимы: создание, редактирование, поиск, манипулирование. Под манипулированием понимаются такие действия с БД, как с целым: просмотр; копирование файлов, например на бумажный носитель; сортировка данных по заданному признаку и т. д.

Для работы с базой данных СУБД должна обеспечивать:

• возможность внесения и чтения информации;

• работу с большим объемом данных;

• быстроту поиска данных;

• целостность данных (их непротиворечивость);

• защиту от разрушения, уничтожения (не только при случайных ошибках пользователя), от несанкционированного доступа;

• систему дружественных подсказок (в расчете на пользователя без специальной подготовки).

СУБД могут использоваться как в однопользовательском, так и в многопользовательском режиме.

На рынке программного обеспечения можно выделить такие наиболее востребованные СУБД, как Microsoft Access, Microsoft Visual FoxPro, Borland dBase, Borland Paradox, Oracle, MySQL.

12.4. Система управления базами данных Microsoft Access

Введение

Microsoft Access обладает всеми чертами классической системы управления базами данных (СУБД). Access – это не только мощная, гибкая и простая в использовании СУБД, но и система для разработки приложений баз данных. К числу наиболее мощных средств Access относятся средства разработки объектов – мастера, которые можно использовать для создания таблиц, запросов, различных типов форм и отчетов.

К областям применения Microsoft Access можно отнести следующие:

• в малом бизнесе (бухгалтерский учет, ввод заказов, ведение информации о клиентах, ведение информации о деловых контактах);

• в работе по контракту (разработка внутриотраслевых приложений, разработка межотраслевых приложений);

• в крупных корпорациях (приложения для рабочих групп, системы обработки информации);

• в качестве персональной СУБД (справочник по адресам, ведение инвестиционного портфеля, поваренная книга, каталоги книг, пластинок, видеофильмов и т. п.).

Рассмотрим основные определения, связанные с разработкой баз данных.

База данных (БД, data base, DB) – совокупность взаимосвязанных данных, используемых под управлением СУБД.

В самом общем смысле база данных – это набор записей и файлов, организованных специальным образом.

Система управления базой данных (СУБД, DBMS) – программная система, обеспечивающая определение физической и логической структуры базы данных, ввод информации и доступ к ней.

Возможности СУБД: система управления базами данных предоставляет возможность контролировать задание структуры и описание данных, работу с ними и организацию коллективного пользования информацией. СУБД также существенно увеличивает возможности и облегчает каталогизацию и ведение больших объемов хранящейся в многочисленных таблицах информации. СУБД включает в себя три основных типа функций: определение (задание структуры и описание) данных, обработки данных и управление данными.

Определение данных. Определяется, какая именно информация будет храниться в базе данных, задается структура данных и их тип (например количество цифр или символов), а также указывается то, как данные будут связаны между собой. Задаются форматы и критерии проверки данных.

Обработка данных. Данные можно обрабатывать различными способами. Можно выбирать любые поля, фильтровать и сортировать данные. Можно объединять данные с другой связанной информацией и вычислять итоговые значения.

Управление данными. Указываются правила доступа к данным, их корректировки и добавления новой информации. Можно также определить правила коллективного пользования данными.

16. Критерии оптимизации. Типы сверток критериев

Критерии оптимизации. Типы сверток критериев

Типы оптимизации

В тестере стратегий предусмотрено два режима оптимизации, переключение между которыми происходит на вкладке"Настройка".

Медленная (полный перебор параметров)

В данном режиме происходит полный перебор всех возможных комбинаций значений входных переменных, выбранных для оптимизации на соответствующей вкладке.

Этот метод является наиболее точным, однако прогоны советника со всеми комбинациями параметров занимают достаточно продолжительное время.

Быстрая (генетический алгоритм)

В основу данного типа оптимизации заложен генетический алгоритм подбора наилучших значений входных параметров. Данный тип оптимизации значительно быстрее полного перебора параметров и практически не уступает ему в качестве. Оптимизация полным перебором, которая заняла бы несколько лет, выполняется за несколько часов при использовании генетического алгоритма.

Каждая особь имеет определенный набор генов, который соответствует набору ее параметров. Генетическая оптимизация основана на постоянном отборе наиболее "приспособленных" параметров (значения, которые дают наилучший итоговый результат). В общем виде алгоритм может быть представлен следующим образом:

•Из общего числа возможных комбинаций параметров случайным образом выбираются две популяции (множества);

•Проводится тестирование обоих множеств, и из них оставляется только одно множество, имеющее наилучшие результаты (по критерию оптимизации);

•Члены данного множества случайным образом скрещиваются между собой, претерпевая случайные мутации и инверсии параметров;

•Потомки сортируются по наилучшим результатам и скрещивание повторяется;

•Операции сортировки и скрещивания продолжаются до тех пор, пока есть улучшение результатов (наилучший результат среди потомков превышает наилучший результат среди родителей). Для окончания оптимизации необходимо отсутствие улучшения критерия оптимизации на протяжении нескольких скрещиваний (поколений).

Количество проходов тестирования

При генетической оптимизации количество проходов тестирования значительно ниже, за счет этого достигается быстрота оптимизации. После запуска генетической оптимизации на вкладке "Настройки"показывается оценочное количество предстоящих проходов тестирования. Оно рассчитывается по следующей формуле:

Размер популяции * (Безусловное количество поколений + Число поколений для оценки сходимости)

где:

•Размер популяции — рассчитывается на основе количества возможных комбинаций оптимизируемых параметров, может принимать значение от 64 до 256;

•Безусловное количество поколений — может принимать значение от 15 до 31. Определяется наличием улучшения критерия оптимизации. 15 поколений проходят тестирование всегда. Если на одном из поколений в промежутке от 15 до 31 не наблюдаются улучшения критерия оптимизации, начинается дополнительной тестирование последующих поколений для оценки сходимости.

•Число поколений для оценки сходимости — число таких поколений рассчитывается как треть от безусловного количества поколений. Если безусловное количество поколений равно 18 (на 17 поколении был лучший результат, а на 18 улучшений не было), то дополнительно тестируются 5 поколений: на 18 поколении уже не было улучшений, а для проверки сходимости необходимо отсутствие улучшений на 18/3 = 6 поколениях. Если на протяжении условного количества поколений не будет выявлено улучшение, то тестирование прекращается.

•Если общее количество шагов оптимизации превышает 1 000 000 в 32-х битной системе или 100 000 000 в 64-х битной системе, то автоматически включается режим быстрой оптимизации. •При генетической оптимизациипромежуточные результаты сохраняются в кэше после расчета каждого поколения (файл папка_данных_терминала/tester/cache/*.gen). Таким образом, процесс генетической оптимизации можно прерывать в любой момент. Даже если процесс генетической оптимизации будет прерван из-за внешних причин (например, отключения электричества), оптимизация будет автоматически продолжена с последнего рассчитанного поколения при последующем запуске. Кэш генетической оптимизации хранится до изменениянастроек оптимизацииили до полного завершения процесса оптимизации. •При штатной остановке оптимизации (кнопкой "Стоп") сохраняются все ранее рассчитанные проходы. При возобновлении оптимизации, процесс будет продолжен с места остановки.

Все символы, выбранные в окне "Обзор рынка"

В отличие от двух предыдущих, данный режим оптимизации позволяет испытать советника с одинаковыми входными параметрами, но на различных символах. При каждом проходе оптимизации изменяется толькоосновной символ тестированиясоветника, иными словами, символ графика, к которому был бы прикреплен советник.

Оптимизация проходит только на тех символах, которые в текущий момент выбраны в окне "Обзор рынка". Таким образом, регулируя набор выбранных символов, можно управлять оптимизацией.

•Следует учитывать, что закачка необходимых ценовых данных с сервера может занимать продолжительное время. Однако замедление процесса оптимизации в результате закачки данных происходит только при первом ее запуске на символе, в последующем докачиваются лишь недостающие данные. •При оптимизации по символам используются текущие значения входных параметров, указанные в колонке "Значение".

Критерий оптимизации

Критерий оптимизации — некий показатель, значение которого определяет качество тестируемого набора входных параметров. Чем больше значение критерия оптимизации, тем лучше оценивается результат тестирования с данным набором параметров. Выбор данного показателя осуществляется на вкладке "Настройки", справа от поля "Оптимизация".

Критерий оптимизации необходим только для генетического алгоритма.

Доступны следующие критерии оптимизации:

•Максимальный баланс — показателем оптимизированности является максимальное значение баланса;

•Баланс + максимальная прибыльность —  показателем является максимальное значение произведения баланса наприбыльность;

•Баланс + максимальное  матожидание выигрыша — показателем является произведение баланса на матожидание выигрыша;

•Баланс + минимальная просадка — в данном случае помимо значения баланса учитывается уровень просадки: (100% - Просадка)*Баланс;

•Баланс + максимальный фактор восстановления — показателем является произведение баланса на фактор восстановления;

•Баланс + максимальный коэффициент Шарпа — показателем является произведение баланса на коэффициент Шарпа;

•Пользовательский критерий оптимизации — при выборе данного параметра в качестве критерия оптимизации будет учитываться значение функции OnTester() в советнике. Данный параметр позволяет пользователю использовать любой собственный показатель для оптимизации.

 

Свертка критериев http://otherreferats.allbest.ru/emodel/00131580_0.html

В многокритериальных задачах, когда из первоначальной постановки не удается выделить критерий, преобладающий по важности над другими - главный критерий, довольно часто критерии искусственно комбинируют посредством агрегирующей функции, с параметрами - весовыми коэффициентами, назначаемыми каждому критерию согласно его относительной важности. Этот подход часто называют скаляризацией или сверткой векторного критерия. А получающуюся при этом параметризованную функцию, сводящую исходную многокритериальную задачу к однокритериальной, - обобщенным, агрегированным, глобальным критерием или суперкритерием. Наиболее широко распространенным видом обобщенного критерия является линейная свертка, когда глобальный критерий представляется в виде суммы (иногда произведения) частных критериев, умноженных на соответствующие весовые коэффициенты.

При применении этого способа определенные трудности вызывает правильный выбор весовых коэффициентов, проблематична интерпретация получаемых результатов. Использовать рассмотренный прием образования обобщенного критерия имеет смысл только в тех случаях, когда интерес представляет сумма отдельных критериальных функций. В общем же случае происходит просто замена одних неопределенностей другими, замаскированная математическими выкладками [2].

Существуют также случаи, когда довольно проблематично назначить каждому критерию определенный весовой коэффициент, соответствующий его важности относительно остальных. Тогда прибегают к свертке критериев где весовые коэффициенты не отражают относительной важности критериев, а изменяясь в определенных пределах, способствуют тем самым локализации точек в множестве Парето. При этом еще больше возрастает роль ЛПР, т.к. при выборе весовых коэффициентов он руководствуется в основном собственным опытом и интуицией, что также требует от него определенной квалификации.

Неоднократно отмечались ошибки и противоречия, которые делает человек при назначении весов критериев. Достаточно обстоятельный обзор различных методов назначения весов подводит к выводу, что не существует корректных методов решения человеком этой задачи. Такое поведение человека при решении многокритериальных зада является повторяющимся и устойчивым.

Имеются результаты экспериментов, из которых следует, что человек назначает веса критериев с существенными ошибками по сравнению с объективно известными, что назначаемые веса противоречат его непосредственным оценкам альтернатив и т.д. Хотя дискуссия о возможности использования весов в методах принятия решений еще продолжается, полученных данных уже достаточно, чтобы считать эту операцию достаточно сложной для ЛПР [4].

Суммируя сказанное можно сделать следующий вывод. Метод сверток применялся и применяется наиболее часто, но имеет труднопреодолимые недостатки [11, 17]:

- не всегда потеря качества по одному критерию компенсируется приращением по другому. «Оптимальное» по свертке решение может характеризоваться низким качеством некоторых частных критериев и в связи с этим будет неприемлемым;

- не всегда можно задать веса критериев. Зачастую известна лишь сопоставимая важность критериев, иногда нет никакой информации о важности;

- результат сильно зависит от предпочтений ЛПР, который чаще всего назначает веса, исходя из интуитивного представления о сравнительной важности критериев;

- величина функции цели, полученная по свертке, не имеет никакого физического смысла;

- многократный запуск алгоритма по свертке может давать только несколько различных точек Парето (или одну и ту же) даже в случае, когда в действительности этих точек очень много;

- данный подход не способен генерировать истинные Парето-оптимальные решения в условиях невыпуклых поисковых пространств, что является серьезным препятствием при решении многих практических задач.

Итак, для решения любой многокритериальной задачи необходимо учитывать сведения об относительной важности частных критериев.

В некоторых многокритериальных задачах частные критерии строго упорядочены по важности так, что следует добиваться приращения более важного критерия за счет любых потерь по всем остальным менее важным критериям. Но в большинстве случаев возникает ситуация, когда выделить главный или упорядочить критерии по важности не удается. Тогда зачастую прибегают к свертке критериев в обобщенный критерий. Применение данного подхода к формированию множества Парето, также как методов последовательных уступок и выделения основного частного критерия, связано с рядом возникающих при этом трудностей, что ставит вопрос о целесообразности использования подобных подходов и необходимости разработки методов, лишенных их недостатков.

К тому же, характерной чертой, объединяющей 3 рассмотренных подхода, является то, что в каждом из них задача многокритериальной оптимизации сводится к одной или нескольким задачам однокритериальной оптимизации.

Таким образом, теряется суть решаемой задачи, ее отличительная особенность - одновременный учет многих критериев. А сами методы должны работать многократно, чтобы сгенерировать множество точек Парето с тем, чтобы дальше выполнить оценку решения, значительно увеличивая затрачиваемые при этом вычислительные ресурсы.

17. Линейное программирование

Задачи линейного программирования относятся к категории оптимизационных. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования. Несмотря на различные области приложения, данные задачи имеют единую постановку: найти значения переменных  x1, …, xn, доставляющие оптимум заданной линейной формы z=c1x1 + c2x2+… + cnxn при выполнении системы ограничений, представляющих собой также линейные формы.

Постановка задачи линейного программирования.

Родоначальником линейного программирования считают д-ра физ.-мат. наук, лауреата Государственной и Нобелевской премий Л.В. Канторовича, который в 30-е годы XX века предложил метод решения экономических задач (в частности, задачи раскроя фанеры). Л.В. Канторович разработал метод разрешающих множителей для решения задачи линейного программирования.

В последующем, в 50-е гг. XX в. независимо от Канторовича метод решения задачи линейного программирования (так называемый симплекс-метод) был развит американским математиком Дж. Данцигом, который в 1951 г. и ввел термин «линейное программирование».

Слово «программирование» объясняется тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно определяют программу (план) действий некоторого объекта, например, промышленного предприятия. Слово «линейное» отражает линейную зависимость между переменными.

Приведем простейший пример задачи линейного программирования.

Предположим, что в трех цехах (Ц1, Ц2, ЦЗ) изготавливается два вида изделий И1 и И2. Известна загрузка каждого цеха аi (оцениваемая в данном случае в процентах) при изготовлении каждого из изделий и прибыль (или цена, объем реализуемой продукции в рублях) сi от реализации изделий. Требуется определить, сколько изделий каждого вида следует производить при возможно более полной загрузке цехов, чтобы получить за рассматриваемый плановый период максимальную прибыль или максимальный объем реализуемой продукции.

Такую ситуацию удобно отобразить в таблице, которая подсказывает характерную для задач математического программирования форму представления задачи, т. е. целевую функцию (в данном случае определяющую максимизацию прибыли или объема реализуемой продукции)

(1)

и ряд ограничений (в данном случае диктуемых возможностями цехов, т.е. их предельной 100%-ной загрузкой)

5 х1 + 4х2 ≤ 100;

1.6 х1+ 17.4 х2 ≤ 100;                                  (2)

2.9 х1 + 5.8 х2 ≤ 100.

Изделие	Цех (участок)				Цена
	Ц1	Ц2	ЦЗ	Изделия
И1	5%	1.6%	2.9%	240 руб.
И2	4%	17.4%	5.8%	320 руб.
Максимальная загрузка	100%	100%	100%

Простые ЗЛП допускают геометрическую интерпретацию, позволяющую непосредственно из графика получить решение и проиллюстрировать идею решения более сложных задач линейного программирования.

Графическое решение задачи приведено на рисунке 8.1.

Ограничения здесь задают область допустимых решений в форме (заштрихованного) четырехугольника, а семейство (пунктирных) прямых, представляет собой линии уровня целевой функции F .

Существует два крайних положения линии уровня, когда она «касается» допустимого множества. Этим двум положениям в данном случае соответствуют две точки «касания» -начало координат (0, 0) и точка (9, 13). Первая из этих точек - точка минимума, а вторая - максимума данной функции F вида (1) на допустимом множестве (2).

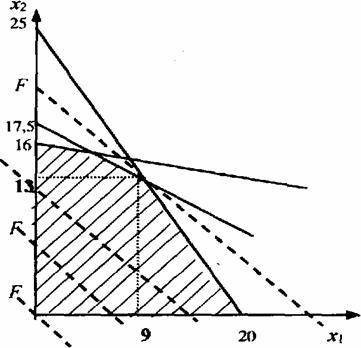
Рис. 8.1. Графическое решение ЗЛП

В случае большего числа разнородных ограничений графическая интерпретация задачи затруднена, поэтому задачу представляют в математической форме и используются специальные методы.

Постановка данной задачи выглядит следующим образом.

Имеется множество переменных X = (x1, х2,..., хn). Целевая функция линейно зависит от управляемых параметров:

(8.1)

Имеются ограничения, которые представляют собой линейные формы

где .         (8.2)

Задача линейного программирования формулируется так:

Определить максимум линейной формы

F(x1,…,xn )=max(c1x1+…+cnxn)   (8.3)

при условии, что точка (х1, х2,..., хn) принадлежит некоторому множеству D, которое определяется системой линейных неравенств

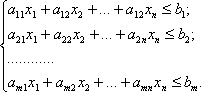(8.4)

Любое множество значений (х1*, х2*,..., хn*), которое удовлетворяет системе неравенств (8.4) задачи линейного программирования, является допустимым решением данной задачи. Если при этом выполняется неравенство

c1х1o+ c2 х2o+..+ cn хno ≥ c1х1+ c2 х2+..+ cn хn

для всего множества значений x1, х2,..., хn, то значение х1o..хno является оптимальным решением задачи линейного программирования.

Задачу линейного программирования удобно представлять в векторной форме, тогда она будет выглядеть следующим образом: найти max F(x) = max (cTx) при условии АХ ≤Ро; Х≥0,

где с = (с1,с2,..., сn) представляет собой n-мерный вектор, составленный из коэффициентов целевой функции, причем сT-транспонированная вектор-строка; х = (х1, х2,..., хп) - п-мерный вектор переменных решений;

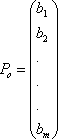- m-мерный вектор свободныхчленов ограничений;

Матрица А размером (m×n) - матрица, составленная из коэффициентов всех линейных ограничений:

Простые ЗЛП допускают геометрическую интерпретацию, позволяющую непосредственно из графика получить решение и проиллюстрировать идею решения более сложных задач линейного программирования.

Каноническая задача линейного программирования заключается в минимизации (максимизации) линейной целевой функции

F(x) = clx1+c2x2+... + cnxn при ограничениях

a11х1 +а12х2 +...+а1пхn=b1

а21х1 +а22х2 +...+а2пхn=b1…

…

аm1х1 +аm2х2 +...+аmпхn=b1

xt,x2,...,xn>0.

где с[,с2,...,сп - коэффициенты целевой функции, atJ, i = \, 2,...,n,j = 1, 2,...,m -коэффициенты системы ограничений, а b1,bг,...,bn - свободные члены, которые считаются неотрицательными.

Вектор X = (xi, х2,..., xj, удовлетворяющий ограничениям задачи ЛП, называется допустимым решением или планом. Допустимый план X* =(xl,x'2,...,x'n), при котором целевая функция задачи ЛП принимает максимальное (минимальное) значение, на­зывается оптимальным планом.

Иными словами, каноническая задача линейного программирования (ЛП) состоит в нахождении среди всех решений выписанной выше системы линейных уравнений такого ее неотрицательного решения, на котором достигает своего минимального (максимального) значения линейная целевая функция z от и переменных.

В задаче линейного программирования общего вида вместо некоторых (всех) равенств в ограничениях записаны нестрогие неравенства в ту или другую сторону; при этом усло­вие неотрицательности переменных может отсутствовать для части или же для всех переменных. Известно, что решение любой задачи линейного программирования может быть сведено к решению канонической задачи, представляемой в форме (1) или (4).

Линейное программирование (ЛП) первоначально развивалось как направление, разрабатывающее новые подходы к решению задач минимизации выпуклых функций на выпуклом множестве (см. выпуклое программирование). Понятие целевой функции , удобное для приложений, сформировалось позднее.

Наиболее простым и распространенным методом решения канонической задачи линейного программирования до сих пор является симплекс-метод, предложенный в 40-е годы прошлого века Дж. Данцигом. Геометрически идею симплекс-метода в упрощенной форме можно выразить следующим образом. Допустимым множеством в задаче линейного программирования является некоторое многогранное множество и-мерного векторного пространства (в частном случае n = 2 - это выпуклый и не обязательно ограниченный многоугольник). Работа симплекс-метода начинается с некоторой начальной вершины (начального опорного плана) многогранного множества. Специальным образом выясняется, нет ли среди соседних вершин такой, в которой значение целевой функции лучше? Если такая вершина находится, то она и принимается за следующее приближение. После этого вновь исследуются соседние вершины для полученного приближения и т. д. до тех пор, пока не будет получена вершина, среди соседних вершин которой не существует вершины с лучшим значением целевой функции. Такая вершина является оптимальной. Она соответствует оптимальной точке (оптимальному решению) задачи линейного программирования.

В настоящее время разработан широкий круг различных численных методов решения задач линейного профаммирования, каждый из которых учитывает ту или иную специфическую особенность имеющейся задачи линейного профаммирования.

Кроме симплекс-метода имеются и другие методы решения специальных задач ЛП: метод потенциалов, Венгерский метод, двойственный симплекс-метод, метод обратной матрицы (модифицированный симплекс-метод) и др.

В настоящее время линейное профаммирование представляет собой область математики, посвященную разработке теории и численных методов решения экстремальных задач с линейными целевыми функциями и линейными ограничениями в виде систем равенств и/или неравенств. С применением линейного программирования решается широкий круг задач экономического характера: задачи о комплексном использовании сырья, рационального раскроя материалов, задачи загрузки оборудования, размещения заказов по однородным предприятиям, задачи о смесях, задачи текущего производственного планирования (статическая модель), задачи перспективного оптимального планирования, транспортная задача .

18. Симплекс метод

В вычислительной схеме симплекс-метода реализуется упорядоченный процесс , при котором , начиная с некоторой исходной допустимой угловой точки ( обычно начало координат ) , осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор , пока не будет найдена точка , соответствующая оптимальному решению .

Общую идею симплекс-метода можно проиллюстрировать на примере модели, посроенной для нашей задачи . Пространство решений этой задачи представим на рис. 1 . Исходной точкой алгоритма является начало координат ( точка А на рис. 1 ) . Решение , соответствующее этой точке, обычно называют начальным решением . От исходной точки осуществляется переход к некоторой смежной угловой точке .

Выбор каждой последующей экстремальной точки при использовании симплекс-метода определяется следующими двумя правилами.

1. Каждая последующая угловая точка должна быть смежной с предыдущей . Этот переход осуществляется по границам ( ребрам ) пространства решений .

2. Обратный переход к предшествующей экстремальной точке не может производиться .

Таким образом , отыскание оптимального решения начинается с некоторой допустимой угловой точки , и все переходы осуществляются только к смежным точкам , причем перед новым переходом каждая из полученных точек проверяется на оптимальность .

Определим пространство решений и угловые точки агебраически . Требуемые соотнощшения устанавливаются из указанного в таблице соответствия геометрических и алгебраических определений.

Геометрическое определение	Алгебраическое определение ( симплекс метод )
Пространство решений	Ограничения модели стандартной формы
Угловые точки	Базисное решение задачи в стандартной форме

Вычислительные процедуры симплекс-метода .

симплекс-алгоритм состоит из следующих шагов.

Шаг 0. Используя линейную модель стандартной формы , определяют начальное допустимое базисное решение путем приравнивания к нулю п — т ( небазисных ) переменных.

Шаг 1. Из числа текущих небазисных ( равных нулю ) переменных выбирается включаемая в новый базис переменная , увеличение которой обеспечивает улучшение значения целевой функции. Если такой переменной нет , вычисления прекращаются , так как текущее базисное решение оптимально . В противном случае осуществляется переход к шагу 2.

Шаг 2. Из числа переменных текущего базиса выбирается исключаемая переменная , которая должна принять нулевое значение ( стать небазисной ) при введении в состав базисных новой переменной .

Шаг 3. Находится новое базисное решение , соответствующее новым составам небазисных и базисных переменных . Осуществляется переход к шагу 1.

Поясним процедуры симплекс-метода на примере решения нашей задачи . Сначала необходимо представить целевую функцию и ограничения модели в стандартной форме:

Z - X1 - 25X2 + 0S1 - 0S2 = 0 ( Целевая функция )

5X1 + 100X2 + S1 = 1000 ( Ограничение )

-X1 + 2X2 + S2 = 0 ( Ограничение )

Как отмечалось ранее , в качестве начального пробного решения используется решение системы уравнений , в которой две переменные принимаются равными нулю . Это обеспечивает единственность и допустимость получаемого решения .

В рассматриваемом случае очевидно, что подстановка X1 = X2 = 0 сразу же приводит к следующему результату: S1 = 1000 , S2 = 0 ( т. е. решению , соответствующему точке А на рис. 1 ) . Поэтому точку А можно использовать как начальное допустимое решение . Величина Z в этой точке равна нулю , так как и X1 и X2 имеют нулевое значение . Поэтому , преобразовав уравнение целевой функции так , чтобы его правая часть стала равной нулю , можно убедиться в том , что правые части уравнений целевой функции и ограничений полностью характеризуют начальное решение . Это имеет место во всех случаях , когда начальный базис состоит из остаточных переменных.

Полученные результаты удобно представить в виде таблицы :

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z	1	-1	- 25	0	0	0	Z – уравнение
S1	0	5	100	1	0	1000	S1 –уравнение
S2	0	-1	2	0	1	0	S2 – уравнение

Эта таблица интерпретируется следующим образом. Столбец « Базисные переменные » содержит переменные пробного базиса S1, S2, значения которых приведены в столбце « Решение » . При этом подразумевается , что небазисные переменные X1 и X2 ( не представленные в первом столбце ) равны нулю . Значение целевой функции Z = 1*0 + 25*0 + 0*1000 + 0*1 равно нулю , что и показано в последнем столбце таблицы .

Определим , является ли полученное пробное решение наилучшим ( оптимальным ) . Анализируя Z - уравнение , нетрудно заметить , что обе небазисные переменные X1 и X2 , равные нулю , имеют отрицательные коэффициенты . Всегда выбирается переменная с большим абсолютным значением отрицательного коэффициента ( в Z - уравнении ), так как практический опыт вычислений показывает , что в этом случае оптимум достигается быстрее. Это правило составляет основу используемого в вычислительной схеме симплекс-метода условия оптимальности , которое состоит в том, что, если в задаче максимизации все небазисные переменные в Z - Уравнение имеют неотрицательные коэффициенты , полученное пробное решение является оптимальным . В противном случае в качестве новой базисной переменной следует выбрать ту , которая имеет наибольший по абсолютной величине отрицательный коэффициент .

Применяя условие оптимальности к исходной таблице , выберем в качестве переменной , включаемой в базис , переменную Х2 . Исключаемая переменная должна быть выбрана из совокупности базисных

переменных S1 , S2 . Процедура выбора исключаемой переменной предполагает проверку условия допустимости, требующего, чтобы в качестве исключаемой переменной выбиралась та из переменных текущего базиса, которая первой обращается в нуль при увеличении включаемой переменной X2 вплоть до значения , соответствующего смежной экстремальной точке .

Интересующее нас отношение ( фиксирующее искомую точку пересечения и идентифицирующее исключаемую переменную ) можно определить из симплекс-таблицы. Для этого в столбце, соответствующем вводимой переменной X2 , вычеркиваются отрицательные и нулевые элементы. Затем вычисляются отношения постоянных, фигурирующих в правых частях этих ограничений , к оставшимся элементам столбца, соответствующего вводимой переменной X2. Исключаемой переменной будет та переменная текущего базиса, для которой указанное выше отношение минимально. Начальная симплекс-таблица для нашей задачи, получаемая после проверки условия допустимости ( т. е. после вычисления соответствующих отношений и определения исключаемой переменной ), воспроизведена ниже. Для удобства описания вычислительных процедур, осуществляемых на следующей итерации, введем ряд необходимых определений. Столбец симплекс таблицы, ассоциированный с вводимой переменной , будем называть ведущим столбцом. Строку,

соответствующую исключаемой переменной , назовем ведущей строкой ( уравнением ), а элемент таблицы, находящийся на пересечении ведущего столбца и ведущей строки, будем называть ведущим элементом .

После того как определены включаемая и исключаемая переменные ( с использованием условий оптимальности и допустимости ), следующая итерация ( поиск нового базисного решения ) осуществляется методом исключения переменных , или методом Гаусса — Жордана . Этот процесс изменения базиса включает вычислительные процедуры двух типов .

Тип 1 ( формирование ведущего уравнения ) .

Новая ведущая строка = Предыдущая ведущая строка / Ведущий элемент

Тип 2 ( формирование всех остальных уравнений , включая Z - yравнение ) .

Новое уравнение = Предыдущее уравнение —

é Коэффициент ù

ê ведущего столбца ê * ( Новая ведущая строка ) .

ê предыдущего ê

ë уравнения û

Выполнение процедуры типа 1 приводит к тому, что в новом ведущем уравнении ведущий элемент становится равным единице. В результате осуществления процедуры типа 2 все остальные коэффициенты, фигурирующие в ведущем столбце, становятся равными нулю. Это эквивалентно получению базисного решения путем исключения вводимой переменной из всех уравнений, кроме ведущего. Применяя к исходной таблице процедуру 1, мы делим S2 - уравнение на ведущий элемент, равный 1.

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z
S1
S2	0	-1/2	1	0	1/2	0

Чтобы составить новую симплекс-таблицу , выполним необходимые вычислительные процедуры типа 2

1. Новое Z - уравнение .

старое Z - уравнение : ( 1 -1 -25 0 0 0 )

( - ( -25 ) * ( 0 -1/2 1 0 1/2 0 )

( 1 -131/2 0 0 121/2 0 )

2. Новое S1 - уравнение

старое S1 - уравнение : ( 0 5 100 1 0 1000 )

( - 100 ) * ( 0 -1/2 1 0 1/2 0 )

( 0 55 0 1 -50 1000 )

Новая симплекс-таблица будет иметь вид:

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z	1	-131/2	0	0	121/2	0	Z – уравнение
S1	0	55	0	1	-50	1000	S1 –уравнение
X2	0	-1/2	1	0	1/2	0	X2 – уравнение

В новом решении X1 = 0 и S2 = 0. Значение Z не изменяется. Заметим, что новая симплекс-таблица обладает такими же характеристиками , как и предыдущая : только небазисные переменные X1 и S2 равны нулю, а значения базисных переменных, как и раньше, представлены в столбце « Решение ». Это в точности соответствует результатам, получаемым при использовании метода Гаусса—Жордана.

Из последней таблицы следует, что на очередной итерации в соответствии с условием оптимальности в качестве вводимой переменной следует выбрать X1, так как коэффициент при этой переменной в Z-ypaвнении равен -131/2 . Исходя из условия допустимости, определяем, что исключаемой переменной будет S1. Отношения, фигурирующие в правой части таблицы, показывают, что в новом базисном решении значение включаемой переменной X1 будет равно 1000/55 ( = минимальному отношению ). Это приводит к увеличению целевой функции на ( 1000/55 ) * ( -131/2 ) = ( 2455/11 ).

К получению симплекс-таблицы , соответствующей новой итерации, приводят следующие вычислительные операции метода Гаусса—Жордана.

1) Новое ведущее S1 - уравнение = Предыдущее S1 - уравнение / ( 55 ) .

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z
S1	0	1	0	1/55	- 50/55	1000/55
X2

2) Новое Z - уравнение = Предыдущее Z - уравнение - ( -131/2) * Новое /ведущее уравнение :

( 1 -131/2 0 0 121/2 0 )- ( -131/2 )

* ( 0 1 0 1/55 -50/55 1000/55 )

( 1 0 0 27/110 5/22 2455/11 )

3) Новое X2 - уравнение = Предыдущее X2 - уравнение - (-1/2 ) * Новое ведущее уравнение :

( 0 -1/2 1 0 1/2 0 )

- ( - 1/2 ) * ( 0 1 0 1/55 -50/55 1000/55 )

( 0 0 1 1/110 1/22 91/11 )

В результате указанных преобразований получим следующую симплекс-таблицу.

Базисные переменные	Z	X1	X2	S1	S2	Решение
Z	1	0	0	27/110	5/22	2455/11
X1	0	1	0	1/55	-50/55	1000/55
X2	0	0	1	1/110	1/22	91/11

В новом базисном решении X1=1000/55 и X2=91/11. Значение Z увеличилось с 0 ( предыдущая симплекс-таблица ) до 2455/11 ( последняя симплекс-таблица ). Этот результирующий прирост целевой функции обусловлен увеличением X1 от О до 1000/55 , так как из Z - строки предыдущей симплекс-таблицы следует , что возрастанию данной переменной на единицу соответствует увеличение целевой функции на( -131/2 ).

Последняя симплекс-таблица соответствует оптимальному решению задачи, так как в Z - уравнении ни одна из небазисных переменных не фигурирует с отрицательным коэффициентом. Получением этой pезультирующей таблицы и завершаются вычислительные процедуры симплекс-метода.

В рассмотренном выше примере алгоритм симплекс-метода использован при решении задачи, в которой целевая функция подлежала максимизации. В случае минимизации целевой функции в этом алгоритме необходимо изменить только условие оптимальности:

в качестве новой базисной переменной следует выбирать ту переменную, которая в Z - уравнении имеет наибольший положительный коэффициент. Условия допустимости в обоих случаях ( максимизации и минимизации ) одинаковы. Представляется целесообразным дать теперь окончательные формулировки обоим условиям, используемым в симплекс-методе.

Условие оптимальности. Вводимой переменной в задаче максимизации ( минимизации ) является небазисная переменная , имеющая в Z -уравнении наибольший отрицательный ( положительный ) коэффициент , В случае равенства таких коэффициентов для нескольких небазисных переменных выбор делается произвольно, если все коэффициенты при небазисных переменных в Z - уравнении неотрицательны (неположительны), полученное решение является оптимальным.

Условие допустимости, в задачах максимизации и минимизации в качестве исключаемой переменной выбирается та базисная переменная, для которой отношение постоянной в правой части соответствующего ограничения к ( положительному ) коэффициенту ведущего столбца минимально. В случае равенства этого отношения для нескольких базисных переменных выбор делается произвольно.

19. Нелинейное программирование

Нелинейное программирование является частью математического программирования, в котором нелинейная функция представлена определенными ограничениями или целевой функцией. Основной задачей нелинейного программирования является нахождение оптимального значения заданной целевой функции с определенным количеством параметров и ограничений.

Задачи нелинейного программирования отличаются от задач линейного содержанием оптимального результата не только в пределах области, имеющей определенные ограничения, но и за ее пределами. К таким типам задач относятся те задания математического программирования, которые могут быть представлены как равенствами, так и неравенствами.

Классифицируется нелинейное программирование в зависимости от разновидности функции F(x), функции ограничений и размерности вектора решений x. Так, название задачи зависит от количества переменных. При использовании одной переменной нелинейное программирование может быть выполнено с помощью безусловной однопараметрической оптимизации. При числе переменных свыше одной можно использовать безусловную многопараметрическую оптимизацию.

Для решения задач линейности используют стандартные методы линейного программирования (например, симплекс-метод). А вот при нелинейном общего способа решения не существует, выбирается в каждом отдельном случае свое и оно также зависит от функции F(x).

Нелинейное программирование встречается в обыденной жизни довольно часто. Например, это непропорциональный рост затрат количеству произведенных или закупленных товаров.

Иногда для нахождения оптимального решения в задачах нелинейного программирования стараются выполнить приближение к линейным задачам. Примером могут служить квадратичное программирование, в котором функция F(x) представлена полиномом второй степени по отношению к переменным, при этом соблюдается линейность ограничений. Вторым примером служит использование метода штрафных функций, применение которых при наличии определенных ограничений сводит задание поиска экстремума к аналогичной процедуре без таковых ограничений, решаемой значительно проще.

Однако если анализировать в целом, то нелинейное программирование представляет собой решение задач повышенной вычислительной трудности. Очень часто во время их решения приходится использовать приближенные методы оптимизации. Еще одно мощное средство, которое может быть предложено для решения такого типа задач – численные методы, позволяющие найти верное решение с заданной точностью.

Как уже было сказано выше, нелинейное программирование требует индивидуального особого подхода, который должен учитывать его специфику.

Существуют следующие методы нелинейного программирования:

- градиентные методы, основанные на свойстве функционального градиента в точке. Другими словами, это вектор частных производных, вычисленный в точке, принятой в качестве указателя направления наибольшего увеличения функции в окрестностях этой точки.

- метод Монте-Карло, при котором определяется параллелепипед n-ой размерности, включающий в себя множество планов, для последующего моделирования случайных N-точек с равномерным распределением в данном параллелепипеде.

- метод динамического программирования сводится к многомерной задаче оптимизации заданий к меньшей размерности.

- метод выпуклого программирования реализуется в поиске минимального значения выпуклой функции или максимального значения вогнутой на выпуклой части множества планов. В случае, когда множество планов представляет собой выпуклый многогранник, тогда может быть применен симплексный метод.

В задаче нелинейного программирования (НЛП) требуется найти значение многомерной переменной х=(), минимизирующее целевую функцию f(x) при условиях, когда на переменную х наложены ограничения типа неравенств

, i=1,2,…,m (1)

а переменные , т.е. компоненты вектора х, неотрицательны:

(2)

Иногда в формулировке задачи ограничения (1) имеют противоположные знаки неравенств. Учитывая, однако, что если , то , всегда можно свести задачу к неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком равенства, например , то их можно представить в виде пары неравенств , , сохранив тем самым типовую формулировку задачи.

20. Метод Кунера-Текера