
- •Содержание
- •Логические основы компьютера
- •Цель работы
- •Логические основы компьютера Понятие логического высказывания
- •Основные логические операции и таблицы истинности
- •Логическое отрицание
- •Логическое умножение
- •Логическое сложение
- •Импликация
- •Эквивалентность
- •Строгая дизъюнкция
- •Логические формулы и функции Логическая формула
- •Определение логической (булевой) функции
- •Законы логики
- •Упрощение логических выражений
- •Построение логических функций на основе математических выражений
- •Методы решения логических задач
- •Решение логических задач средствами алгебры логики
- •Решение логических задач табличным способом
- •Решение логических задач с помощью рассуждений
- •Логические элементы компьютера Понятие вентиля
- •Построение логических схем
- •Вопросы для самоконтроля
- •Задачи и упражнения
- •Рекомендуемая литература
- •Логические основы компьютера
- •654007, Г. Новокузнецк, ул. Кирова,42
Определение логической (булевой) функции
Функция в алгебре высказываний f(x1, x2, ..., xn) – это логическая формула, содержащая логические переменные x1, x2, ..., xn, связанные между собой логическими операциями. Как аргументы x1, x2, ..., xn (независимые переменные), так и сама функция (зависимая переменная) принимают значения 0 или 1. Логические функции могут быть заданы табличным способом или аналитически — в виде соответствующих формул.
Если функция задаётся аналитически, то пишется её имя, затем в круглых скобках перечисляются аргументы функции, после чего пишется знак равно и формула функции (аргументы, соединённые знаками логических операций). Например, функции, заданные аналитически:
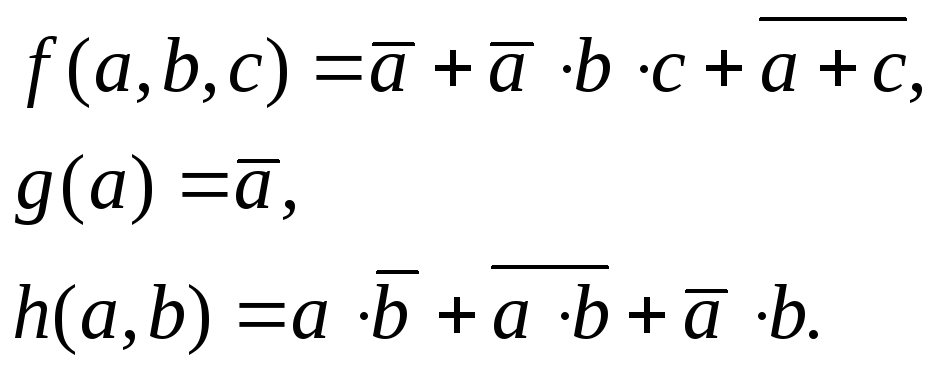
По
формуле логической функции легко
рассчитать ее таблицу истинности.
Необходимо только учитывать порядок
выполнения логических операций
(приоритет) и скобки. Операции
в логическом выражении выполняются
слева направо с учетом скобок.
Для уменьшения количества скобок в
формулах вводят «старшинство» для
знаков логических операций. Принято
считать, что знак
дизъюнкции (+) старше знаков импликации,
эквивалентности и строгой дизъюнкции
(→, ↔,
![]() ),
знак конъюнкции (∙) старше всех
перечисленных, а знак инверсии ( ‾ )
старше всех остальных. При наличии
скобок сначала операции выполняются
операции внутри самых внутренних скобок
согласно приоритету, затем во внешних
скобках и т.д.
),
знак конъюнкции (∙) старше всех
перечисленных, а знак инверсии ( ‾ )
старше всех остальных. При наличии
скобок сначала операции выполняются
операции внутри самых внутренних скобок
согласно приоритету, затем во внешних
скобках и т.д.
Таблица истинности логической функции
Построение таблицы истинности логической функции покажем на примере следующей функции:
![]()
Построение таблицы включает следующие действия:
подсчёт количества аргументов у функции и количество операций, после чего строится таблица с суммарным количеством столбцов. В данном случае количество аргументов три плюс три операции, следовательно, таблица должна включать шесть колонок. Левые колонки отводятся под аргументы функции и обозначаются именами аргументов.
определяется количество строк в таблице по формуле K=2n , где n — количество логических переменных. В данном случае
K = 23 = 8.
определяется последовательность выполнения логических операций и остальные столбцы обозначаются выражением с определённой операцией.
Заполняем столбцы с аргументами наборами значений.
Заполняем столбцы с промежуточными формулами и функцией значениями, используя таблицы истинности логических операций.
|
Аргументы |
Промежуточные формулы |
Функция | |||
|
A |
B |
C |
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
Таким образом, для любой функции можно построить таблицу истинности, используя таблицы истинности логических операций.
Законы логики
Если у двух логических функций совпадают таблицы истинности, то есть на всех наборах значений входных переменных они принимают одинаковое значение, то их называют равносильными или эквивалентными. Это обозначается знаком = (равно).
Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, которые по аналогии с алгеброй вещественных чисел будем называть законами:
Переместительный закон (закон коммутативности):
a + b = b + a, a∙b = b ∙a. (4)
Сочетательный закон (закон ассоциативности):
(a + b) + c = a + (b + c), (5)
(a∙ b)∙ c = a∙ (b∙ c). (6)
Закон исключения констант (нуля и единицы):
a +0 = a, A∙1=A. (7)
Распределительный закон (закон дистрибутивности):
(a + b)∙ c = a∙ c + b∙c, (8)
(a + c)∙ (b + c) = a∙b + c, (9)
(a![]() b)∙
c
= a∙
c
b)∙
c
= a∙
c
![]() b∙c. (10)
b∙c. (10)
Закон противоречия:
![]()
![]() (11)
(11)
Закон равносильности (идемпотентности):
![]()
![]() .
(12)
.
(12)
Закон
двойного отрицания: ![]() (13)
(13)
Закон инверсии (формулы де Моргана):
![]() (14)
(14)
![]() (15)
(15)
Закон поглощения:
![]() (16)
(16)
![]() (17)
(17)
Закон склеивания (закон исключения):
![]() (18)
(18)
![]() (19)
(19)
Любой из этих законов может быть легко доказан с помощью таблиц истинности.
Докажем первый закон де Моргана (14) с использованием таблиц истинности. Построим таблицы истинности для левой и правой частей закона.
-
a
b
a+b
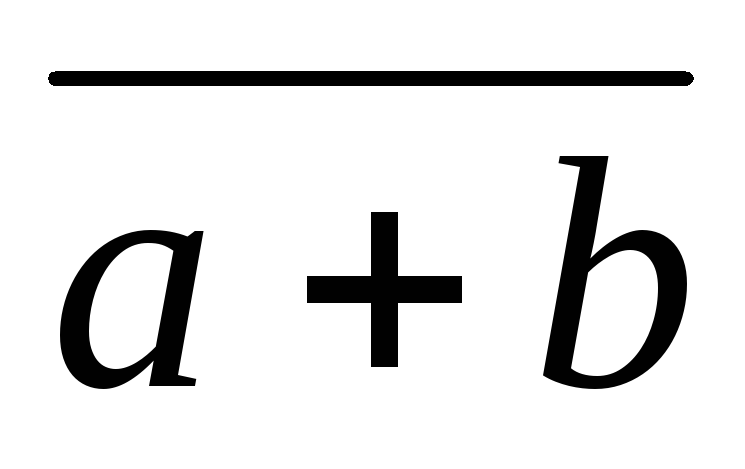

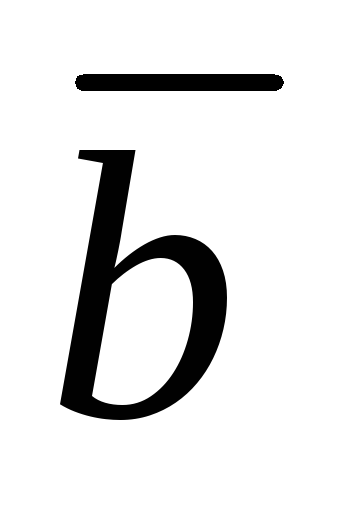
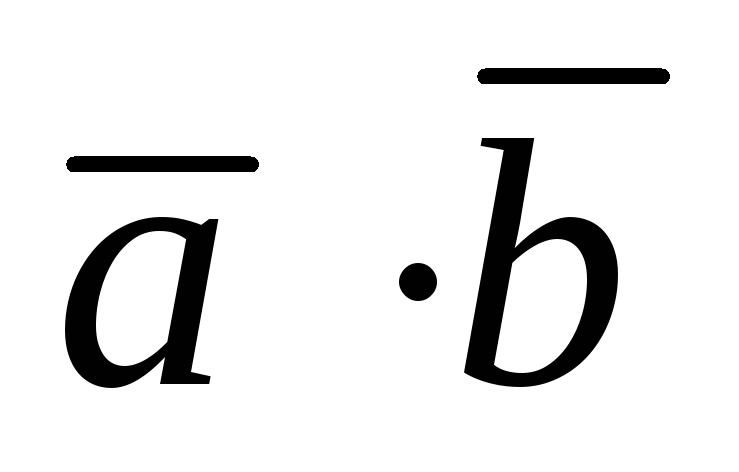
0
0
0
1
1
1
1
0
1
1
0
1
0
0
1
0
1
0
0
1
0
1
1
1
0
0
0
0
Так
как результирующие столбцы (![]() и
и
![]() )
совпали,
то формулы, стоящие в левой и правой
частях закона, равносильны.
)
совпали,
то формулы, стоящие в левой и правой
частях закона, равносильны.
Любой из законов алгебры высказываний может быть доказан путем логических рассуждений.
Докажем
ещё один закон поглощения
![]() путем логических рассуждений. Для этого
достаточно показать, что если правая
часть истинна, то и левая часть истинна,
и что если левая часть истинна, то и
правая часть истинна.
путем логических рассуждений. Для этого
достаточно показать, что если правая
часть истинна, то и левая часть истинна,
и что если левая часть истинна, то и
правая часть истинна.
Пусть
истинна правая часть, т. е. A
=
1, тогда в левой части дизъюнкция
![]() истинна
по определению дизъюнкции. Пусть истинна
левая часть. Тогда по определению
дизъюнкции истинна или формула A,
или
формула
истинна
по определению дизъюнкции. Пусть истинна
левая часть. Тогда по определению
дизъюнкции истинна или формула A,
или
формула
![]() ,
или
обе эти формулы одновременно. Если A
ложна,
тогда
,
или
обе эти формулы одновременно. Если A
ложна,
тогда
![]() ложна.
Следовательно, A
может
быть только истинной.
ложна.
Следовательно, A
может
быть только истинной.
Еще одним способом вывода новых формул являются тождественные преобразования. Например, тот же закон поглощения можно вывести при помощи законов исключения единицы и дистрибутивности:
![]()
Для операций импликации, эквивалентности и строгой дизъюнкции также может быть сформулирован ряд важных свойств. В частности, каждая из этих операций может быть выражена через конъюнкцию, дизъюнкцию и отрицание. Убедитесь в этом, доказав самостоятельно следующие соотношения:
Представление импликации через конъюнкцию,
дизъюнкцию и инверсию:
![]() .
(20)
.
(20)
Представление эквивалентности через
конъюнкцию,
дизъюнкцию и инверсию: ![]() .
(21)
.
(21)
Представление строгой дизъюнкции через
конъюнкцию, дизъюнкцию и инверсию:
![]() (22)
(22)
Правило
контрапозиции (перевертывания):
![]() . (23)
. (23)
Свойства импликации:
![]() (24)
(24)
Свойства эквивалентности:
![]() (25)
(25)
![]() (26)
(26)
Свойства строгой дизъюнкции:
![]() (27)
(27)
