27.4. Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов – процесс гибели и размножения. Название этого процесса связано с биологией, где этот процесс представляет собой математическую модель численности биологических видов.

Размеченный граф состояний процесса гибели и размножения имеет вид, изображенный на рис.27.2.

₀₁

₂₃

_k-1,k

_k,k+1

_n-1,n

S₀

S₁

S₂

S_k

S_n





₁₂





₁₀

₂₁

₃₂

_k,k-1

_k+1,k

_n,n-1

Рис.27.2. Размеченный граф состояний процесса гибели и размножения

Переходы в рассматриваемой системе могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния S_k возможны переходы только в состояние S_k-1 или в состояние S_k+1.

Предположим, что все потоки событий, переводящие систему по стрелкам графа, являются простейшими. Составим и решим алгебраические уравнения для предельных вероятностей состояний.

Согласно правилу составления таких уравнений:

Для состояния S₀:

Для состояния S₁: .

С учетом предыдущего равенства после раскрытия скобок слагаемые и взаимно уничтожаются и уравнение для S₂ имеет вид:

.

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему:

,

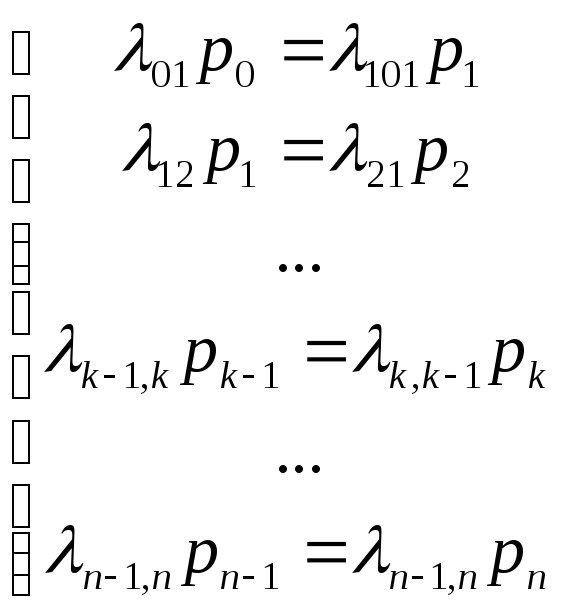к которой добавляется условие нормировки

.

Решая полученную систему уравнений, можно получить:

.

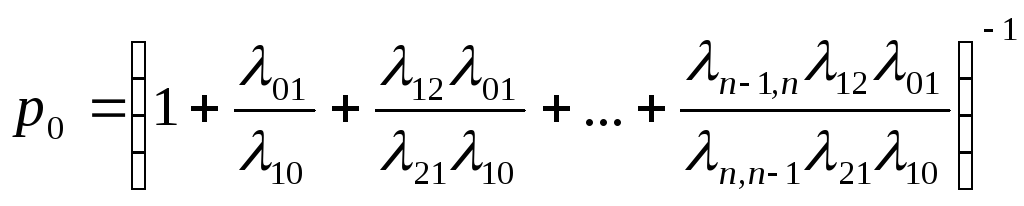
Пример. Решить предыдущую задачу, используя теорию процесса гибели и размножения.

Решение. Размеченный граф состояний имеет вид:

.

.

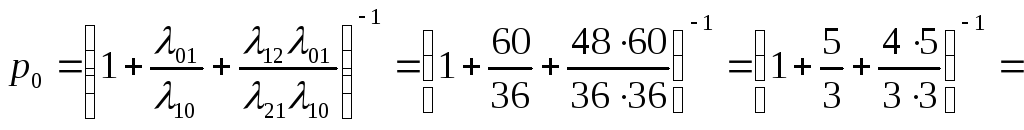
27.5. Системы массового обслуживания с отказами

Пусть имеется одноканальная СМО с отказами, в которую поступает поток заявок с интенсивностью . Обозначим поток обслуживания . Здесь и далее будем предполагать, что все потоки в СМО простейшие. Если заявка поступает в момент, когда единственный канал занят, то она получает отказ и в дальнейшей работе СМО не участвует. Требуется определить предельные вероятности состояний такой СМО и показатели ее эффективности.

СМО имеет два состояния: S₀ – канал свободен и S₁ – канал занят (рис.27.3).

S₀

S₁





Рис.27.3. Одноканальная СМО с отказами

Система алгебраических уравнений для предельных вероятностей состояний такой СМО имеет вид:

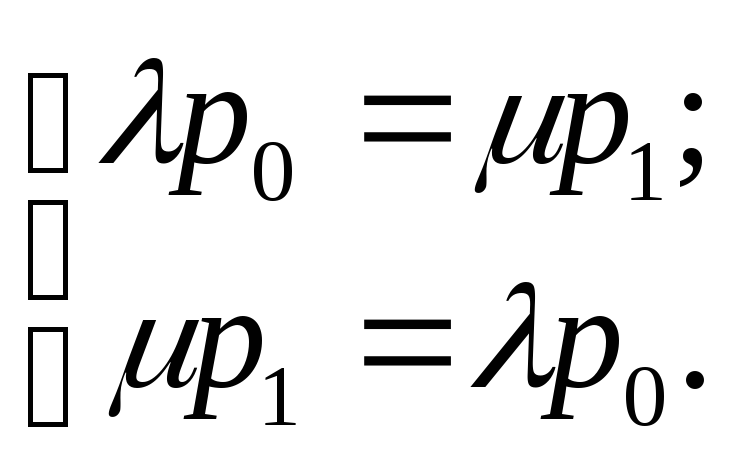
То есть, по существу, имеем одно уравнение. Добавляя к нему условие нормировки p₀ + p₁ = 1, найдем предельные вероятности состояний:

,

которые показывают среднее относительное время пребывания СМО в соответствующих состояниях. Очевидно, что вероятность отказа P_отк равна относительному времени, в течение которого канал занят, т.е.

.

Относительная пропускная способность Q представляет собой вероятность, что заявка будет обслужена, т.е.

.

Абсолютную пропускную способность СМО найдем, умножив Q на интенсивность потока заявок :

.

Рассмотрим теперь многоканальную СМО с отказами. Пусть в СМО имеется n каналов, на которые поступает поток заявок с интенсивностью . Поток обслуживания имеет интенсивность .

СМО может иметь следующие состояния: S₀, S₁, S₂, … S_k, … S_n, где S_k – состояние СМО, когда в ней находится k заявок, т.е. k каналов заняты.

Граф состояний СМО соответствует процессу гибели и размножения (рис.27.4).











S₀

S₁

S₂

S_k

S_n













2

3

k

(k+1)

n

Рис.27.4. Многоканальная СМО с отказами

Поток заявок последовательно переводит систему из левого состояния в соседнее правое с одной и той же интенсивностью . Интенсивность же потока обслуживания зависит от состояния. Если СМО находится в состоянии S₂ (заняты 2 канала), то она может перейти в состояние S₁ когда закончат обслуживание либо первый, либо второй занятый канал. Следовательно, суммарная интенсивность потока обслуживания будет 2 и т.д.

Из формул для предельных вероятностей состояний для процесса гибели и размножения, обозначив , не трудно получить предельные вероятности состояний для рассматриваемой СМО.

;

Эти формулы предельных вероятностей многоканальной СМО с отказами называются формулами Эрланга.

Запишем основные показатели эффективного функционирования многоканальной СМО с отказами:

• Вероятность отказа СМО – это предельная вероятность того, что все n каналов заняты, т.е.

.

• Относительная пропускная способность – вероятность того, что заявка будет обслужена:

.

• Абсолютная пропускная способность

.

• Среднее число занятых каналов 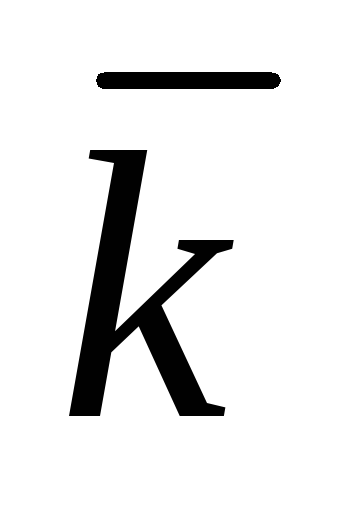- это математическое ожидание числа занятых каналов, которое определяется по известной формуле математического ожидания:

.

Величину можно найти проще. Так как каждый занятый канал обслуживает в среднем  заявок в единицу времени, то

.

Пример. Торговая фирма выполняет заказы на приобретение товаров по телефону. В настоящее время в офисе фирмы установлен 1 телефон. Интенсивность входящего потока заявок составляет 30 заявок в час. Длительность оформления заказа, в среднем, составляет 5 мин. Определить показатели эффективности такой СМО. Сколько телефонов нужно поставить в офисе, чтобы относительная пропускная способность СМО была не менее 0,75.

Решение. Интенсивность потока заявок  = 30 заявок/час. Найдем интенсивность потока обслуживания :

Вероятность отказа:

.

Относительная пропускная способность:

.

Абсолютная пропускная способность:

Чтобы найти, при каком минимальном количестве телефонов относительная пропускная способность будет не менее 0,75, будем постепенно увеличивать число телефонов в офисе и по вышеуказанным формулам определять относительную пропускную способность:

1) n = 2 ; ;

;

.

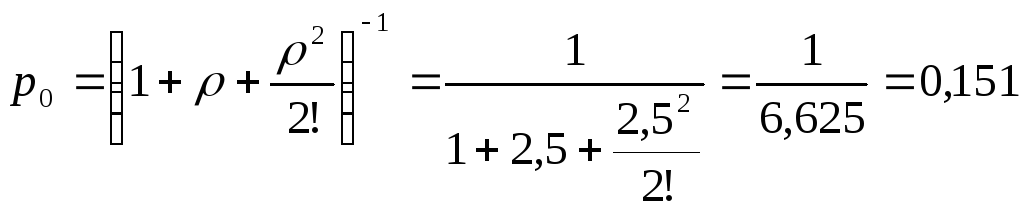2) n = 3 ;

;

.

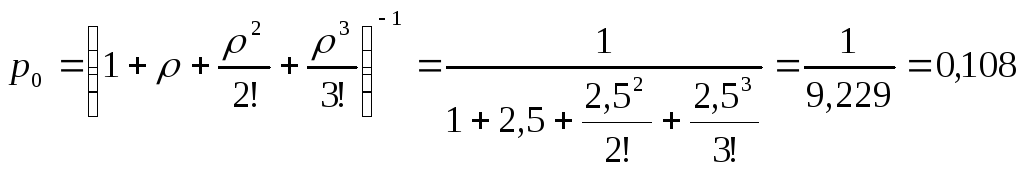3) n = 4 ;

;

.

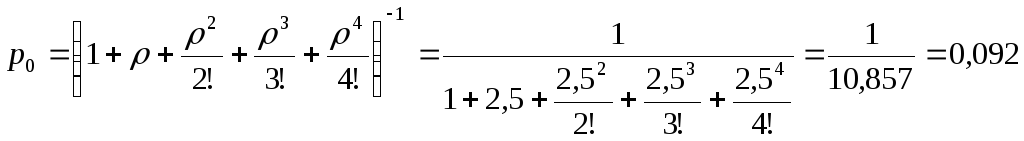Из решения следует, что чтобы относительная пропускная способность СМО была не менее 0, 75, в офисе должно быть не менее 4 телефонов.

27.6. Системы массового обслуживания с ожиданием

Пусть имеется одноканальная СМО с неограниченной очередью (например, телефон-автомат с одной будкой). То есть, на СМО не наложены никакие ограничения ни по длине очереди, ни по времени ожидания. Поток заявок, поступающих в СМО, имеет интенсивность , а поток обслуживания – интенсивность . Необходимо найти предельные вероятности состояний и показатели эффективности СМО.

Система может находиться в одном из состояний S₀, S₁, S₂, …, S_k , … по числу заявок, находящихся в СМО:

S₀ – канал свободен;

S₁ – канал занят, обслуживает заявку, очереди нет;

S₂ – канал занят, в очереди одна заявка;

…

S_k – канал занят, в очереди k – 1 заявка;

…

Размеченный граф состояний СМО имеет вид, изображенный на рис.27.5.

S₀

S₁

S₂

S_k

    

…

    

Рис.27.5. Одноканальная СМО с ожиданием

Это процесс гибели и размножения, но с бесконечным числом состояний. Для такого процесса доказано, что если

,

т.е. если среднее число приходящих заявок в единицу времени меньше среднего числа обслуживаемых заявок, то предельные вероятности существуют. Если   1, то очередь растет до бесконечности.

Для определения предельных вероятностей состояний можно воспользоваться формулами для процесса гибели и размножения (хотя они были получены для случая конечного числа состояний системы, ими можно воспользоваться и в данном случае). Тогда

.

Предельные вероятности могут существовать лишь при  < 1. В этом случае ряд, стоящий в скобках, сходится к сумме , т.к. это геометрический ряд со знаменателем меньшим, чем единица. Поэтому

,

а предельные вероятности других состояний определяются по формулам:

; ; … …

Предельные вероятности состояний образуют убывающую геометрическую прогрессию со знаменателем  < 1, следовательно, вероятность p₀ – наибольшая. Это значит, что если СМО справляется с потоком заявок, то наиболее вероятным состоянием СМО будет отсутствие заявок в системе.

Среднее число заявок в системе L_сист определяется по формуле математического ожидания:

.

Можно показать, что эта формула преобразуется при  < 1 к виду:

.

Среднее число заявок, находящихся под обслуживанием L_об также легко определить по формуле для математического ожидания:

.

Среднее число заявок в очереди L_оч, очевидно, определяется как разность L_сист и L_об:

.

Среднее время пребывания заявки в системе T_сист или в очереди T_оч равно среднему числу заявок в системе или в очереди, деленному на интенсивность потока заявок (формулы Литтла):

;

.

Пример. Мини-маркет с одним контролером-кассиром обслуживает покупателей, интенсивность входящего потока которых равна 20 покупателей/час. Интенсивность потока обслуживания равна 25 покупателей в час. Найти показатели эффективности СМО, а также вероятность, что в очереди стоят не более 2 покупателей.

Решение.

; .

Вероятность, что контролер-кассир свободен:

.

Вероятность, что он занят P_зан равна:

.

Среднее число покупателей в очереди:

.

Среднее число покупателей в мини-маркете:

.

Среднее время простоя в очереди:

.

Среднее время нахождения в мини-маркете:

.

Вероятность, что в очереди не более 2 покупателей определяется по формуле

.