
Математика-2
.PDFМАТЕМАТИКА
Часть 2
♦ ИЗДАТЕЛЬСТВО ТГТУ ♦
Министерство образования и науки Российской Федерации
Тамбовский государственный технический университет
МАТЕМАТИКА
Часть 2
Учебные задания для студентов 1 курса инженерных и экономических специальностей
Тамбов ♦ Издательство ТГТУ ♦
2004
УДК 51(07) ББК В11я73-5
М34
Утверждено Редакционно-издательским советом университета
Рецензент
Доктор физико-математических наук, профессор
А.И. Булгаков
Составители:
А.В. Медведев, В.А. Попов, И.В. Петрова, А.В. Урусов, А.В. Щербакова
М34 Математика: Учебные задания. Ч. 2 / Сост.: А.В. Медведев, В.А. Попов, И.В. Петрова, А.В. Урусов, А.В. Щербакова. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2004. 24 с.
Учебное издание охватывает следующие разделы учебных программ для технических и экономических специальностей: «Матрицы. Определители. Системы линейных алгебраических уравнений», «Линейная алгебра», «Векторная алгебра», «Аналитическая геометрия на плоскости» и «Аналитическая геометрия в пространстве». Предложенные задачи являются типовыми, предназначены для аудиторной и самостоятельной работы студентов, а также могут служить основой при составлении вариантов проверочных заданий.
Предназначено для студентов 1 курса инженерных и экономических специальностей.
УДК 51(07) ББК В11я73-5
©Тамбовский государственный технический университет (ТГТУ), 2004
Учебное издание
МАТЕМАТИКА
Часть 2
Учебные задания
Составители: МЕДВЕДЕВ Александр Васильевич, ПОПОВ Вячеслав Александрович, ПЕТРОВА Ирина Владимировна, УРУСОВ Александр Иванович, ЩЕРБАКОВА Антонина Васильевна
Редактор В.Н. Митрофанова Инженер по компьютерному макетированию Т.А. Сынкова
Подписано к печати 27.12.2004 Формат 60 × 84 / 16. Бумага газетная. Печать офсетная
Гарнитура Тimes New Roman. Объем: 1,39 усл. печ. л.; 1,2 уч.-изд. л.
Тираж 500 экз. С. 903
Издательско-полиграфический центр Тамбовского государственного технического университета
392000, Тамбов, Советская, 106, к. 14
МАТРИЦЫ. ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
1 Даны матрицы А, В, С и число q. Вычислить |
|
|
|
|
|||||||||
1) |
B A ; 2) det (B A) ; 3) A B ; 4) A B +q C ; 5) det C ; 6) |
A ; 7) A−1 , если |
|||||||||||
|
1 |
−1 |
−2 |
1 |
2 |
−3 3 |
|
−2 |
|||||
|
|
|
|
|
|
|
|
||||||
а) |
q = −3 , A = 2 |
−3 , |
|
|
|
|
|
|
C = −2 3 |
|
3 ; |
||
B = |
−4 |
|
|
, |
|
||||||||
|
|
|
|
−3 −1 |
|
−7 |
|
|
|
||||
|
7 |
−2 |
|
|
|
|
|
|
7 |
|
4 |
||
|
−2 |
−3 |
−4 |
3 −6 |
8 |
3 |
|
5 |
|||||
|
|
|
|
|
|
|
|
||||||
б) |
q = 2 , A = 1 |
2 , |
|
|
|
|
|
C = −5 4 |
−5 ; |
||||
B = |
−5 |
1 −3 |
, |
||||||||||
|
|
|
|
|
|
−7 |
|
8 |
|
||||
|
4 |
−2 |
|
|
|
|
|
|
8 |
|
|
||
|
−5 |
−3 |
|
|
−4 1 |
3 |
7 |
9 |
|
−7 |
|||
|
|
|
|
|
|
|
|
|
|
||||
в) |
q = −2 , A = 6 |
1 , |
B = |
|
|
|
|
, C = −5 −4 |
|
8 ; |
|||
|
−2 |
|
|
||||||||||
|
|
|
|
|
3 |
2 |
|
|
|
|
|
||
|
−2 |
4 |
|
|
|
|
|
|
−2 −7 |
−4 |
|||
|
−3 |
4 |
|
|
7 |
1 |
−3 |
−3 2 |
7 |
||||
|
|
|
|
|
|
|
|
|
|||||
г) |
q = 3 , A = 2 |
3 , |
|
|
|
|
|
C = −6 5 |
2 ; |
||||
B = |
−4 |
3 |
, |
||||||||||
|
|
|
|
2 |
|
−2 |
−4 |
|
|||||
|
1 |
−6 |
|
|
|
|
|
|
3 |
|
|||
|
−4 |
−5 |
|
|
3 |
2 |
−1 |
4 |
5 |
|
3 |
||
|
|
|
|
|
|
|
|
|
|
||||
д) |
q = −1 , A = 3 |
2 , |
B = |
|
|
|
|
C = −4 −5 |
|
2 ; |
|||
|
−3 |
4 |
, |
|
|||||||||
|
|
|
|
|
7 |
|
|
−4 |
|
2 |
|
||
|
2 |
−3 |
|
|
|
|
|
|
−3 |
|
|
||
|
3 |
−5 |
|
6 |
−2 |
1 |
|
−7 −5 |
6 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
е) |
q = −4 , A = −1 |
6 , |
B = |
|
|
|
, |
C = 9 |
2 |
6 . |
|||
|
−4 |
|
|||||||||||
|
|
|
|
5 |
4 |
|
|
−6 |
9 |
|
|
||
|
1 |
−2 |
|
|
|
|
|
|
−7 |
|
|
||
2 Вычислить определитель матрицы А двумя способами: 1) получением нулей в i-й строке и разложением по элементам этой строки; 2) получением нулей в j-м столбце и разложением по элементам этого столбца, если
|
−2 |
−4 |
|
−3 |
|
3 |
|
|||||
|
|
−4 |
−3 |
|
2 |
|
− |
2 |
|
|
||
а) i = 2, j = 3, |
|
|
|
|
; |
|||||||
A = |
2 |
1 |
|
2 |
|
− |
2 |
|
||||
|
|
|
|
|
|
|||||||
|
|
−3 |
−1 |
|
4 |
|
− |
2 |
|
|
||
|
|
|
|
|
|
|||||||
|
−3 |
−1 |
|
−1 |
|
4 |
|
|
|
|||
|
|
−1 |
−2 |
|
−1 |
|
1 |
|
|
|
|
|
б) i = 3, j = 1, |
|
|
|
|
; |
|
||||||
A = |
−4 |
−2 |
|
4 |
|
4 |
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
−2 |
1 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
2 |
4 |
4 |
|
|
|
|
|
|||
|
|
3 |
4 |
1 |
1 |
|
|
|
|
|
|
|
в) i = 4, j = 2, |
|
|
|
; |
|
|
|
|||||
A = |
3 |
−2 |
4 |
−2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
2 |
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
−1 |
3 |
|
3 |
−2 |
|
||||||
|
|
−3 |
3 |
−2 |
− |
2 |
|
|
||||
г) i = 2, j = 3, |
|
|
|
|||||||||
A = |
4 |
−1 |
|
4 |
|
2 |
|
; |
||||
|
|
|
|
|
|
|
||||||
|
|
3 |
1 |
|
2 |
|
1 |
|
|
|
||
|
|
|
|
|
|
|
||||||
|
3 |
2 |
−1 |
−1 |
|
||
|
|
−2 |
2 |
−2 |
2 |
|
|
д) i = 3, j = 1, |
|
|
; |
||||
A = |
−4 |
3 |
−4 |
3 |
|
||
|
|
|
|
||||
|
|
3 |
1 |
4 |
4 |
|
|
|
|
|
|
||||
|
3 |
3 |
2 |
−3 |
|
|
|
|
|
4 |
−1 |
1 |
1 |
|
|
е) i = 1, j = 4, |
|
|
|
||||
A = |
4 |
−2 |
4 |
−2 |
. |
||
|
|
|
|
||||
|
|
−1 |
−4 |
2 |
−2 |
|
|
|
|
|
|
||||
3 Решить следующие системы линейных алгебраических уравнений тремя способами (методом Гаусса, методом Крамера, матричным методом):
−5x +3y +5z =12,
а) 7x −5y −7z = −20, б)8x −3y −9z = −14;
−6x −3y +8z =−12, г) −2x +7y −6z =54, д)
−2x +9y −8z =68;
−9x +5y +8z = −5, ж) −7x +4 y +6z = −4,
9x −9 y −4z =13.
8x −5y −7z = 7 ,3x +4 y −6z = 22,
7x +4 y +5z = −30;
−2x −3y +3z = 4,−3x +5y +2z =−25,
5x −9y −3z = 44;
4 |
Решить матричное уравнение A X = B |
||||||||
а) |
−7 |
4 |
, |
28 |
9 |
; б) |
2 |
3 |
, |
A = |
|
B = |
|
A = |
|
||||
|
−3 |
1 |
|
9 |
1 |
|
5 |
4 |
|
−3x −4 y −7z = −4, в) 9x +2 y +6z = −8,−4x +7 y +9z =19;
−4x +3y +7z = −38, е) 5x +2y +4z =8,
−7x +4y +9z = −56;
, где А, В, Х– матрицы, если
4 |
−7 |
|
; |
|
B = |
3 |
−7 |
|
|
|
|
|
||
|
3 |
−2 |
|
10 |
11 |
|
−2 |
−3 |
3 |
|
−11 −9 |
13 |
|
|||
в) |
, |
; г) A= |
|
−3 |
5 |
2 , |
B= |
|
−9 8 |
12 |
; |
|||||
A = |
|
B = |
|
|||||||||||||
|
4 |
3 |
|
2 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 −9 |
|
|
|
14 −15 |
|
|
||||||
|
|
|
|
|
|
|
|
−3 |
|
|
−19 |
|
||||
|
−4 |
−7 7 |
|
|
20 |
25 −18 |
|
||||||
д) |
|
−5 |
−3 7 |
|
, |
B = |
|
10 |
26 −15 |
|
; |
||
A = |
|
|
|
||||||||||
|
|
−4 |
−3 6 |
|
|
|
|
10 |
22 −13 |
|
|
||
|
|
|
|
|
|
|
|
||||||
|
3 4 |
−9 |
|
|
6 |
−38 10 |
|
|
|||||
е) |
|
4 5 |
8 |
|
, |
|
|
47 |
10 13 |
|
; |
|
|
A = |
|
|
B = |
|
|
||||||||
|
|
3 4 |
−5 |
|
|
|
|
14 |
−26 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
7 |
5 |
|
|
|
34 |
6 |
17 |
||||
ж) |
|
−5 |
−8 |
2 |
|
, |
B = |
|
−23 −15 |
−4 |
|
||
A = |
|
|
. |
||||||||||
|
|
3 |
5 |
3 |
|
|
|
|
23 |
5 |
11 |
|
|
|
|
|
|
|
|
|
|||||||
5 Найти решения следующих систем уравнений:
2x −3y +4z =13,
а) −2x +5y +2z = −3,−2x −2 y +3z = 6,
3x +3y −4z = −8,
|
−4x −3y +2z = −15, |
|
б) |
|
4x + y +5z = −1, |
|
||
|
|
3x +2 y + z = 6, |
|
|
2x +4 y −3z =14, |
|
|
|
−3x +3y −2z = 0,
в) −2x +4 y +3z =13,7x −7 y +4z = −2,
5x −2 y +2z = −4,
г)
е)
з)
к)
|
5x +2 y +3z = 4, |
2x −3y +2z −5w = −8, |
|
|||
|
|
|
||||
−3x +3y + z = −1, д) |
|
−5x −2 y −5z +3w =3, |
|
|||
|
−x +2 y + z = 0, |
|
3x +7 y +3z +4w =11, |
|
||
|
|
|
|
|||
|
6x +3y +4z =5, |
|
|
|
|
|
|
|
|
|
|
|
|
4x −4 y +3z −2w = −1, |
|
2x +3y −6z −4w =11, |
||||
|
|
|
|
|
|
|
3x −2 y −2z −4w = −3, ж) |
−3x +4 y +10z −2w =9, |
|||||
|
|
|
|
|
|
|
−5x +7 y −4z +3w =5, |
|
4x −3y −8z +3w = −5, |
||||
|
4x +8y +3z −2w =8, |
|
|
3x +2 y +4z +4w = 7, |
||
|
|
|
+4 y +5z −3w |
= −1, |
||
|
3x +2 y −4z +3w =11 |
|
и) |
2x |
||
|
|
4x |
+3y +3z +2w |
= −6, |
||
|
|
|
|
|||
−2x +5y +7z +2w = 7, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
3x +4 y +3z −3w = 0, |
||
2x +3y +4z +5w =3, |
|
|
|
|
|
|
|
3x +2 y +2z +4w = 2, |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
−5x −2 y +3z −2w =5, |
|
|
|
|
||
|
4x −9 y +5z +3w = 26 |
|
|
|
|
|
|
|
|
|
|
||
Линейная алгебра
1Образует ли множество векторов на плоскости, начала которых находятся в начале координат, а концы – в пределах первой четверти, линейное пространство (с обычными операциями)?
2Образует ли линейное пространство множество всех векторов на плоскости с исключением векторов, параллельных некоторой заданной прямой?
3Рассмотрим совокупность P одних положительных вещественных чисел. Введем операции по следующим правилам: под «сложением» двух чисел будем понимать их обычное умножение, а под про-
изведением элемента r P на вещественное число λ будем понимать (обычное) возведение числа r в степень λ. Является ли Р с указанными операциями линейным пространством?
4Может ли линейное пространство состоять: 1) из одного вектора; 2) из двух различных векторов?
5Задано множество всевозможных упорядоченных систем действительных чисел (x1; x2; ...; xn), (y1; y2; ...; yn), (z1; z2; ...; zn), ... . Сумма двух любых элементов определяется равенством (x1; x2; ...; xn) + (y1; y2;
...; yn) = = (x1 + y1; x2 + y2; ...; xn + yn), а произведение любого элемента на любое действительное число – равенст-
вом λ(x1; x2; ...; xn) = (λx1; λx2; ...; λxn). Доказать, что это множество является линейным пространством.
6Образует ли линейное пространство множество всевозможных упорядоченных систем действи-
тельных чисел вида (x1; x2; 0; 0), (y1; y2; 0; 0), (z1; z2; 0; 0), ... . Сложение элементов и умножение элементов на действительное число определяется так же как в задаче 5.
7Образует ли линейное пространство множество всевозможных упорядоченных систем действи-
тельных чисел вида (x1; x2; 1; 1), (y1; y2; 1; 1), (z1; z2; 1; 1), ... . Сложение элементов и умножение элементов на действительное число определяется так же как в задаче 5.
8Является ли линейным пространством множество всех многочленов не выше второй степени.
9Является ли линейным пространством множество всех многочленов второй степени.
10Заданы функции f1(x), f2(x), f3(x), ... . Является ли множество этих функций линейным пространством, если эти функции образуют:
а) совокупность всех непрерывных функций на отрезке [a, b];
б) совокупность всех дифференцируемых функций на отрезке [a, b]; в) совокупность всех элементарных функций.
11Образует ли линейное пространство множество всех квадратных матриц размера 2 × 2. Сложение элементов и умножение элементов на действительное число определяется по правилам проведения линейных операций над матрицами.
|
|
|
|
Образует ли линейное пространство множество всех квадратных матриц вида |
x |
0 |
|
, |
y |
0 |
|
, |
|||
|
|
12 |
|
|
1 |
|
|
|
1 |
|
|
||||
|
|
|
|
0 |
x2 |
|
|
0 |
y2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
z |
0 |
|
, … . Сложение элементов и умножение элементов на действительное число определяется по |
||||||||||||
|
1 |
|
|
||||||||||||
|
0 |
z2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
правилам проведения линейных операций над матрицами. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Образует ли линейное пространство множество всех квадратных матриц вида |
x |
1 |
|
, |
y |
1 |
|
, |
|||
|
|
13 |
|
|
1 |
|
|
|
1 |
|
|
||||
|
|
|
|
1 |
x2 |
|
|
1 |
y2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
z |
1 |
|
, … . Сложение элементов и умножение элементов на действительное число определяется по |
||||||||||||
|
1 |
|
|
||||||||||||
|
1 |
z2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
правилам проведения линейных операций над матрицами. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
14 |
|
Доказать, что множество всех решений системы линейных однородных |
уравнений |
||||||||||
a x +b y +c z = 0, |
образует линейное пространство. |
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
||
a2 x +b2 y +c2 z = 0 |
|
|
|
|
|
|
|
|
|
|
|
||||
15Из линейного пространства исключен вектор x. Может ли полученное после этого исключения множество векторов являться линейным пространством.
16Доказать, что если среди векторов x, y, z, ... имеется нуль-вектор, то рассматриваемые векторы линейно зависимы.
17Рассматривается линейное пространство многочленов не выше второй степени. Являются ли
векторы |
Р1 |
= |
1 |
+ |
2t |
+ |
3t2, |
Р2 |
= |
2 |
+ |
3t |
+ |
4t2, |
Р3 = 3 + 5t + 7t2 линейно зависимыми. |
|
|
|
|
|
|
|
|
|
|
||||
18Рассматривается линейное пространство многочленов не выше второй степени. Являются ли векторы Р1 = 1 + 2t2, Р2 = 1 + 3t, Р3 = 4 + t линейно зависимыми.
19Рассматривается линейное пространство квадратных матриц второго порядка. Являются ли век-
торы e1 |
1 |
4 |
, e2 |
0 |
1 |
, e3 |
3 |
−1 |
, e4 |
−2 |
0 |
линейно зависимыми. |
|||||||
= |
|
|
|
= |
|
|
= |
|
|
|
= |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
6 |
|
|
|
3 |
−1 |
|
|
2 |
0 |
|
|
|
1 |
1 |
|
|
20 Рассматривается линейное пространство квадратных матриц второго порядка. Являются ли век-
торы e1 |
1 |
1 |
, e2 |
0 |
1 |
, |
e3 |
1 |
2 |
, e4 |
4 |
3 |
линейно зависимыми. |
||||||
= |
|
|
= |
|
|
= |
|
|
|
= |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
3 |
−1 |
|
|
|
5 |
2 |
|
|
|
1 |
1 |
|
|
21 Выяснить, будут ли векторы а1 = (1, 0, 1), а2 = (1, 1, 2), а3 = (2, 1, 2) линейно зависимыми или линейно независимыми.
22 Выяснить, будут ли векторы а1 = (1, 1, 1, 1), а2 = (1, 2, 1, 2),
а3 = (3, 1, 3, 1), а4 = (0, 1, 0, 1) линейно зависимыми или линейно независимыми.
23Доказать, что система векторов, содержащая два равных вектора, линейно зависима.
24Найти все значения λ, при которых вектор b = (7, –2, λ) линейно выражается через векторы а1 = (2, 3, 5), а2 = (3, 7, 8), а3 = (1, –6, 1).
25Найти разложение вектора x в базисе векторов p, q, r, если:
а) x = {–2, 4, 7}, p = {0, 1, 2}, q = {1, 0, 1}, r = {–1, 2, 4}; |
|
|
|
|
|
||||||||
б) x = {6, 12, –1}, p = {1, 3, 0}, q = {2, –1, 1}, r = {0, –1, 2}; |
|
|
|
|
|
||||||||
в) x = {1, –4, 4}, p = {2, 1, –1}, q = {0, 3, 2}, r = {1, –1, 1}; |
|
|
|
|
|
||||||||
г) x = {–9, 5, 5}, p = {4, 1, 1}, q = {2, 0, –3}, r = {–1, 2, 1}. |
|
|
|
|
|
||||||||
26 |
Рассматривается линейное пространство многочленов не выше второй степени. Найти коорди- |
||||||||||||
наты |
многочлена |
Р |
= |
|
8 |
+ |
2t |
+ |
6t2 |
в |
базисе |
||
Р1 = 1 + t + t2, Р2 = 1 + t, Р3 = 1. |
|
|
|
|
|
|
|
|
|
|
|||
27 |
Рассматривается линейное пространство многочленов не выше третьей степени. Найти коорди- |
||||||||||||
наты многочлена Р = 4 – 3t + 3t2 + t3 в базисе |
Р1 = 1 + t + t2 + t3, |
Р2 = 1 + t + t2, Р3 = 1 + t, |
Р4 = 1. |
||||||||||
28 |
Рассматривается линейное пространство квадратных матриц второго порядка. Найти координа- |
||||||||||||
|
1 |
−4 |
в базисе e1 |
0 |
0 |
0 |
0 |
0 1 |
1 1 |
|
|
||
ты матрицы e = |
|
= |
, e2 = |
, e3 |
= |
, e4 |
= |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
8 |
|
0 |
1 |
1 |
1 |
1 1 |
1 1 |
|
|
||
29 |
Рассматривается линейное пространство квадратных матриц второго порядка. Найти координа- |
||||||||||||
|
−3 |
7 |
в базисе e1 |
2 |
−1 |
0 |
1 |
1 |
2 |
−2 0 |
|
|
|
ты матрицы e = |
|
= |
, |
e2 = |
, |
e3 = |
, |
e4 = |
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
14 |
|
0 |
6 |
−1 2 |
2 |
0 |
|
4 1 |
|
|
|
30 |
Выяснить, какие из преобразований (операторов) Аx являются линейными и для линейных пре- |
||||||||||||
образований векторов x = (x1, x2, x3) найти их матрицу: |
|
|
|
|
|
|
|||||||
а) Аx = (x2 + x3, 2x1 + x3, 3x1 – x2 + x3); |
б) Аx = (x1, x2 + 1, x3 + 1). |
|
|
|
|||||||||
31 |
Будут ли линейными операторами в пространстве всех многочленов от t: |
|
|
||||||||||
|
а) |
умножение на t; |
б) |
умножение на t2; |
в) дифференцирование. |
|
|
|
|
|
|
|
|||||||
|
32 |
Будут ли линейными операторами в пространстве квадратных матриц: |
|
|
|
|
|
|
|||||||||||
|
а) умножение матрицы на элемент матрицы а11; |
|
|
|
|
|
|
|
|
|
|
||||||||
|
б) умножение матрицы на наибольший элемент матрицы. |
|
|
|
|
|
|
|
|
|
|||||||||
|
33 |
В четырехмерном линейном пространстве рассматривается линейное преобразование А. Напи- |
|||||||||||||||||
сать это преобразование в координатной форме, если Ае1 = е3 + е4, |
Ае2 = е1 + е4, Ае3 = е2 + е4, |
Ае4 = е2 |
|||||||||||||||||
+ е3. |
|
Пусть в базисе е1, е2, е3 заданны линейно независимые векторы а1, а2, а3. Найти линейное преоб- |
|||||||||||||||||
|
34 |
||||||||||||||||||
разование, |
|
|
переводящее |
|
векторы |
|
|
а1, |
|
|
а2, |
|
|
а3 |
|||||
соответственно в |
b1, |
b2, |
b3, если |
а1 |
= (2, 3, |
5), а2 |
= |
(0, |
1, |
2), |
а3 |
= |
(1, |
0, |
0), |
||||
b1 = (1, 1, 1), b2 = (1, 1, –1), b3 = (2, 1, 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
35 |
Найти линейное преобразование, переводящее векторы а1 = (2, 0, 3), а2 = (4, 1, 5), |
а3 = (3, 1, 2) |
со- |
|||||||||||||||
ответственно |
|
в |
|
векторы |
b1 |
|
= |
|
(1, |
|
|
2, |
|
–1), |
|||||
b2 = (4, 5, –2), b3 = (1, –1, 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
36 |
Пусть в базисе е1, е2, е3 задан вектор x = (6, 1, –3). Найти координаты |
вектора |
x в |
базисе |
век- |
|||||||||||||
торов |
e'1, |
e'2, |
e'3, |
|
если |
e'1 |
= |
е1 |
+ |
|
е2 |
+ |
|
2е3, |
|||||
e'2 = 2е1 – е2, e'3 = –е1 + е2 + е3. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
37 |
Пусть в базисе е1, е2, е3 задан вектор x = (1, 2, 4). Найти координаты |
вектора |
x в базисе векто- |
|||||||||||||||
ров |
|
|
|
e'1, |
|
e'2, |
e'3, |
|
если |
e'1 |
= |
е1 |
+ |
|
е2 |
+ |
|
3е3, |
|
e'2 = 1,5е1 – е2, e'3 = –е1 + е2 + е3. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
38 |
Найти характеристические числа и собственные векторы линейного преобразования с матрицей |
|||||||||||||||||
|
6 |
−4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
Найти характеристические числа и собственные векторы линейного преобразования с матрицей |
|||||||||||||||||
|
2 |
−1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
|
−1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
40 |
Найти характеристические числа и собственные векторы линейного преобразования с матрицей |
|||||||||||||||||
|
4 |
−2 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A = |
|
−1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Векторная алгебра
1 По данным векторам a и b построить следующие векторы: 1) 2a; 2) –0,5b; 3) 3a + 0,25b; 4) 0,5a – 3b.
2Даны: |a| = 13, |b| = 19 и |a + b| = 24. Вычислить |a – b|.
3Даны: |a| = 11, |b| = 23 и |a – b| = 30. Вычислить |a + b|.
4Даны вершины А(3, 2, –5), В(1, 4, 3) и С(–3, 0, 1) треугольника. Найти координаты середин его сторон.
5Даны вершины А(2, –1, 4), В(3, 2, –6) и С(–5, 0, 2) треугольника. Вычислить длину медианы, проведенной из вершины А.
6Даны три вершины А(3, –1, 2), В(1, 2, –4) и С(–1, 1, 2) параллелограмма. Найти его четвертую вершину D.
7Отрезок прямой, ограниченный точками А(–1, 8, 3) и В(9, –7, 2) разделен точками на пять равных частей. Найти координаты этих точек.
8 Определить при каких значениях α и β векторы a = {–2, 3, β} и b = {α, –6, 2} коллинеарны.
9Проверить, что четыре точки А(3, –1, 2), В(1, 2, –1), С(–1, 1, 3) и D(3, –5, 3) служат вершинами трапеции.
10Даны два вектора a = {3, –2, 6} и b = {–2, 1, 0}. Определить координаты следующих векторов:
1) |
a + b; |
2) |
a – b; |
3) |
2a; |
4) 2a + 3b; |
5) 0,5a – b. |
11 |
Даны два вектора a = {2, 4, 3} и b = {–1, 5, 8}. Определить координаты следующих векторов: |
||||||
1) |
a + b; |
2) |
a – b; |
3) |
3a; |
4) a + 2b; |
5) 0,5a – 3b. |
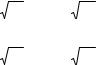
12 |
Векторы |
a |
и |
b |
образуют |
угол |
ϕ = |
|
π |
; |
|
зная, |
|
что |
|a| |
= |
3 |
и |
|b| |
= |
4, |
||
3 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) ab; 2) a2; 3) b2; 4) (a + b)2; 5) (3a + 2b)(a – b); 6) (a – b)2. |
|
|
|
|
|
|
|
||||||||||||||||
13 |
Векторы |
a |
и |
b |
образуют |
угол |
ϕ = |
2π |
; |
зная, |
|
что |
|a| |
= |
5 |
и |
|b| |
= |
3, |
||||
3 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) ab; 2) a2; 3) b2; 4) (a + b)2; 5) (3a + 2b)(a – b); 6) (a – b)2. |
|
|
|
|
|
|
|
||||||||||||||||
14 |
Даны векторы a = {4, –2, –4} и b = {6, –3, 2}. Вычислить: |
|
|
|
|
|
|
|
|
|
|||||||||||||
1) ab; 2) |
a2 ; 3) |
b2 ; 4) (2a – 3b)(а + b); 5) (a + b)2. |
|
|
|
|
|
|
|
|
|
||||||||||||
15 |
Даны векторы a = {2, 4, 4} и b = {2, –6, 3}. Вычислить: |
|
|
|
|
|
|
|
|
|
|||||||||||||
1) ab; 2) |
a2 ; 3) |
b2 ; 4) (3a + 2b)(а – b); 5) (a – b)2. |
|
|
|
|
|
|
|
|
|
||||||||||||
16 |
Даны вершины четырехугольника А(1, –2, 2), В(1, 4, 0), С(–4, 1, 1) и D(–5, –5, 3). Доказать, что |
||||||||||||||||||||||
его диагонали АС и ВD взаимно перпендикулярны. |
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
17 |
Вычислить |
проекцию |
вектора |
|
= |
{5, |
2, |
5} |
|
на |
|
ось |
|
вектора |
|||||||||
b = {2, –1, 2} и найти косинус угла между этими векторами. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
18 |
Вычислить |
проекцию |
вектора |
|
a |
= |
{6, |
3, |
2} |
|
на |
|
ось |
|
вектора |
||||||||
b = {2, 2, 1} и найти косинус угла между этими векторами. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
19 |
Даны вершины А(–1, –2, 4), В(–4, –2, 0) и С(3, –2, 1) треугольника. Определить его внутренний |
||||||||||||||||||||||
угол при вершине В. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
20 |
Даны три вектора a = {2, –1, –3}, b = {1, –3, 2} и с = {3, –4, 12}. Найти вектор x, удовлетворяю- |
||||||||||||||||||||||
щий условиям: xa = –5, xb = –11, xc = 20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
21 |
Определить и построить вектор c = a × b, если: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1) a = 3i, b = 2k; 2) a = i + j, b = i – j; 3) a = 2i + 3j, b = 3j + 2k. |
|
|
|
|
|
|
|
||||||||||||||||
22 |
Раскрыть скобки и упростить выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1)i × (j + k) – j × (i + k) + k × (i + j + k);
2)(a + b + c) × c + (a + b + c) × b + (b – c) × a;
3)(2a + b) × (c – a) + (b + c) × (a + b);
4)2i (j × k) + 3j (i × k)+ 4k (i × j).
23 |
Векторы |
a и b образуют |
угол |
ϕ = |
2π |
; зная, что |a| = 1 и |b| = 2, |
|
||||||
|
|
|
|
3 |
|
|
вычислить: |
|
|
|
|
|
|
1) |
|a × b|2; |
2) |(3a + 2b) × (a – b)|2; |
3) |(a + 3b) × (3a – b)|2. |
|||
24 |
Даны векторы a = {3, –1, –2} и b = {1, –2, –1}. Вычислить: |
|||||
1) a × b; 2) (2a + b) × b; 3) (3a + 2b) × (а – b). |
||||||
25 |
Даны векторы a = {1, 1, –3} и b = {3, 2, 0}. Вычислить: |
|||||
1) a × b; 2) (a + 3b) × b; 3) (a + 2b) × (а – 3b). |
||||||
26 |
Построить параллелограмм на векторах a = 2j + k и b = i + 2k и вычислить его площадь и высоту. |
|||||
27 |
Даны вершины А(1, –2, 8), В(0, 0, 4) и С(6, 2, 0) треугольника. Вычислить его площадь и длину |
|||||
высоты, опущенной из вершины В на сторону АС. |
|
|
|
|||
28 |
Даны вершины А(1, –1, 2), В(5, –6, 2) и С(1, 3, –1) треугольника. Вычислить его площадь и длину |
|||||
высоты, опущенной из вершины В на сторону АС. |
|
|
|
|||
29 |
С помощью векторного произведения выяснить, коллинеарны ли векторы a = {1, 0, 3} и b = {2, 0, |
|||||
6}. |
|
|
|
|
|
|
30 Векторы a, b и с, образующую правую тройку, взаимно перпендикулярны. Зная, что |a| = 4, |b| = 2 и |с| = 3, вычислить abс.
31 Вектор с перпендикулярен к векторам a и b, угол между векторами a и b равен 30°. Зная, что |a| = 6, |b| = 3 и |с| = 3, вычислить abс.
32 Даны три вектора a = {0, 1, –3}, b = {3, 2, 1}, с = {1, 3, 2}. Вычислить abс. 33 Установить, компланарны ли векторы:
a = {2, 3, –1}, |
b = {1, |
–1, 3}, |
с = {1, 9, –11}; |
|
|
|
|
|
|
|
|
||
a = {1, 1, –3}, |
b = {0, |
1, 0}, с = {1, 1, 1}; |
|
|
|
|
|
|
|
|
|
||
a = {2, –1, 2}, |
b = {1, |
2, –3}, |
с = {3, –4, 7}. |
|
|
|
|
|
|
|
|
||
34 |
Доказать, |
что |
четыре |
точки |
А(1, |
2, |
–1), |
В(0, |
1, |
5), |
С(–1, |
2, |
1), |
D(2, 1, 3) лежат в одной плоскости. |
|
|
|
|
|
|
|
|
|
||||
35 |
Вычислить объем пирамиды, вершины которой находятся в точках А(5, 2, 0), |
В(2, 5, 0), |
С(1, 2, |
||||||||||
4), D(0, 0, 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
36 |
Даны вершины |
пирамиды: |
А(2, |
3, |
1), |
В(4, |
1, |
–2), |
С(6, |
3, |
7), |
||
D(–5, –4, 8). Найти длину |
высоты, опущенной из вершины D. |
|
|
|
|
|
|
||||||
ПРЯМАЯ НА ПЛОСКОСТИ
1В треугольнике АВС составить уравнения медианы и высоты, проведенных из вершины А. А(–4; 2), В(–7; 7), С(–13; –13).
2В треугольнике АВС составить уравнение прямой, проходящей через вершину А перпендикуляр-
но медиане ВМ. А(0; 4), В(2; 6), С(8; –2).
3В треугольнике АВС найти проекцию вершины В на сторону АС. А(2; 4), В(4; 10), С(6; –2).
4 Составить |
уравнения |
прямых, |
проходящих |
через |
точку |
А(2; 1): |
|
|
|
|
|
а) параллельно прямой 3x + 2y – 5 = 0; |
|
|
|
||
б) перпендикулярно прямой A(2; 1) |
3х + 4у – 2 = 0. |
|
|
|
|
5Зная координаты вершины A(1; 3) треугольника АВС и уравнения двух его медиан х – 2у + 1 = 0;
у– 1 = 0 составить уравнения всех сторон треугольника.
6Пусть стороны АВ, ВС и АС треугольника АВС лежат на прямых, имеющих следующие уравнения: х + у + 1 = 0; х + 6у + 1 = 0. Составить уравнения высоты, проведенной из вершины А.
7Пусть стороны АВ, ВС и АС треугольника АВС лежат на прямых, имеющих следующие уравнения: 2х + у – 2 = 0; 5х + у – 2 = 0; x = 1. Написать уравнение медианы, проведенной из вершины В.
8Найти точку В* симметричную точке В(3; 5) относительно прямой, проходящей через точки А(0; 1) и С(8; –3).
9 Даны |
координаты |
вершин |
четырехугольника |
АВСD: |
А(0; 1), |
В(3; 6), С(8; 2), D(5; –2). Найти угол между диагональю АС и стороной АD. |
|
|
|||
10 Даны |
вершина А(2; |
6) треугольника |
АВС и уравнения |
высот y |
= x |
и y = –2x, проходящих через вершины В и С. Написать уравнение стороны ВС треугольника АВС. |
|
||||
11Одна из сторон квадрата лежит на прямой 3x + 2y – 7 = 0, а координаты одной из вершин квадрата A(–2; 3). Найти площадь этого квадрата.
12Одна из вершин квадрата А(1; 2) лежит на стороне, уравнение которой 2x + y – 4 = 0. Написать уравнение диагонали квадрата, выходящей из точки А.
13Найти точку А* симметричную точке А(2; 4) относительно прямой 2x + 3y – 12 = 0. Сделать чер-
теж.
14В треугольнике АВС: А(–2; 2), В(2; 5), С(6; –4). Написать уравнение биссектрисы, выходящей из вершины А.
15Даны координаты трех последовательных вершин параллелограмма АВСD: А(–4; 2), В(0; 6), С(6; –2). Найти координаты вершины D. Написать уравнение диагонали ВD.
16Написать уравнение прямой, проходящей через точку А(2; –3) и точку М, делящую отрезок ВС в
отношении 3 : 2, где В(4; 1), С(6; 4).
17 Найти точку пересечения медиан треугольника АВС: А(0; 2),
В(4; 1), С(2; –6).
КРИВЫЕ ВТОРОГО ПОРЯДКА
Привести уравнение линии к каноническому виду, определить тип линии, найти эксцентриситет, координаты фокусов(а). Изобразить эту линию.
1)4x2 +25y2 +32x −150 y +189 = 0 .
2)4x2 +16 y2 +8x −160 y +340 = 0 .
3)x2 −2x +6 y +7 = 0 .
