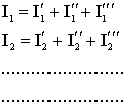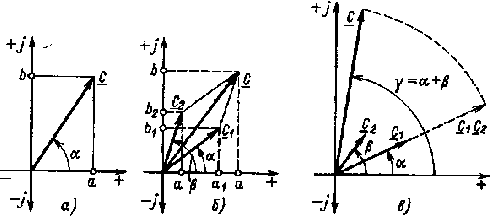elektrotekhnika
.doc|
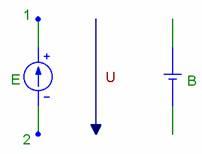
1. Источники напряжения и тока, их свойства, характеристики и схемы замещения. Законы Ома и Кирхгофа. Источник ЭДС характеризуется величиной ЭДС равной напряжению (разности потенциалов) на зажимах при отсутствии тока через источник. ЭДС определяют как работу сторонних сил, присущих источнику, на перемещение единичного положительного заряда внутри источника от зажима с меньшим потенциалом к зажиму с большим потенциалом.
Напряжение на зажимах реального источника зависит от тока через источник. Если этой зависимостью можно пренебречь, то такой источник называют идеальным. Для реальных источников запишем закон Ома для полной цепи:
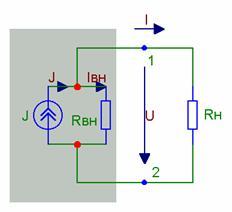
Напряжение U на зажимах реального источника меньше ЭДС на величину падения напряжения на внутреннем сопротивлении. Идеальный источник имеет Rвн=0. Максимальный ток возникает в режиме короткого замыкания при Rн=0, при этом выходное напряжение U стремится также к нулю. Источник тока Источник тока характеризуется током I при короткозамкнутых зажимах (при отсутствии напряжения). Если ток не зависит от напряжения - такой источник называют идеальным.
Ток I реального источника энергии зависит от напряжения U на его зажимах. Из закона Ома для полной цепи:
|
В этой схеме элемент gвн параллельно соединенный с идеальным источником J, называют внутренней проводимостью. Идеальный источник тока имеет gвн=0 (то есть Rвн=∞). Обобщенный закон Ома для участка цепи с ЭДС
Вывод: ток участка цепи с источниками ЭДС равен алгебраической сумме его напряжения и ЭДС, деленной на сопротивление участка. Законы Кирхгофа и их применение Определения: Ветвью электрической цепи называется участок, состоящий из последовательно включенных источников ЭДС и приемником с одним и тем же током. Узлом называется место или точка соединения трех и более ветвей. Контур - замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза Режим цепи произвольной конфигурации определяется первым и вторым законами Кирхгофа. Первый закон Кирхгофа Применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю. Знаки определяются в зависимости от того, направлен ток к узлу или от него (в любом случае произвольно).
Применяется к контурам: в любом контуре сумма напряжений на всех элементах и участках цепи, входящих в этот контур, равна нулю. Направление обхода каждого контура можно выбирать произвольно. Знаки определяются в зависимости от совпадения напряжений с направлением обхода. Вторая формулировка: в любом замкнутом контуре алгебраическая сумма напряжений на всех участках с сопротивлениями, входящих в этот контур, равно алгебраической сумме ЭДС.
|
|
|
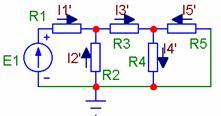
2, Методы расчета сложных электрических цепей постоянного тока: метод непосредственного применения законов Кирхгофа. Пусть У - количество узлов цепи, В - количество ветвей, К - число контуров.
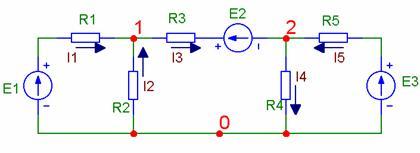
Линейная разветвленная электрическая цепь (У=3, В=5, K=6)
|
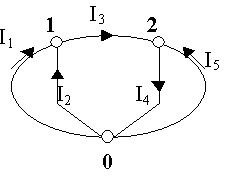
Упрощенная схема цепи (узлы 0, 1, 2) По первому закону Кирхгофа для каждого из узлов:
Таким образом, число независимых уравнений при решении по методу Кирхгофа равно У-1+В-У+1=В. Для решения составляют матрицу и решают методом Крамера. Недостаток - много уравнений.
|
|
|
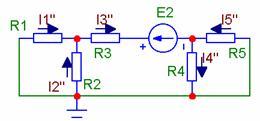
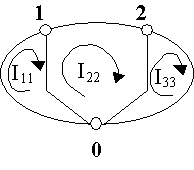
3, Метод контурных токов. Для данной схемы примем одинаковое направление обхода контуров. Обозначим контурные токи I11, I22, I33 -для 1, 2 и 3 контуров.
Контурные токи будут равны токам в тех ветвях, которые не входят в два контура, то есть I11= I1, I22= I3, I33= -I5. Из уравнений, составленных по первому закону Кирхгофа, выразим токи, принадлежащие смежным ветвям (то есть I2 и I4) и подставим в уравнения, составленные по второму закону Кирхгофа:
|
Выполним замены для контурных токов и запишем в матричном виде:
В данной матрице сопротивления с одинаковыми индексами называют собственным сопротивлением контура - сумма всех сопротивлений контура. С двумя разными индексами - общим сопротивлением соответствующих контуров (пишется со знаком минус). Правая часть уравнения называется контурной ЭДС - она равна алгебраической сумме ЭДС всех источников в ветвях контура. Знак определяется в соответствии с направлениями. Находят I11, I22, I33 методом Крамера, далее:
методом контурных токов решают K=(В-У+1) уравнений |
|
|
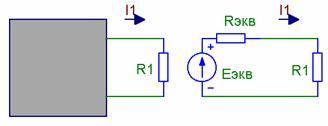
4. Метод эквивалентного преобразования цепи. Метод эквивалентного преобразования схемы используют при расчете простых электрических цепей. В отдельных случаях имеется возможность применить его и для расчета сложных электрических цепей. Суть метода эквивалентного преобразования схемы заключается в упрощении схемы, когда два (или несколько) однотипных элемента электрической цепи замещаются одним эквивалентным элементом того же типа. Под термином "эквивалентный элемент" подразумевается такой элемент, замещение на который не меняет значений токов и напряжений в остальной части электрической цепи. Схематичный пример использования метода эквивалентного преобразования схемы для расчета сложной электрической цепи изображен ниже:
|
|
|
|
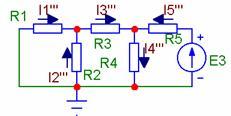
5. Метод узловых потенциалов Для схемы предыдущего примера составим уравнения для токов через разность потенциалов на узлах:
|
В матричной форме:
Элементы матрицы с одинаковыми индексами содержат суммы проводимостей ветвей, соединенных с данным узлом. Элементы матрицы с разными индексами содержат проводимости ветвей между соответствующими узлами со знаком минус. Правая часть каждого из уравнений равна алгебраической сумме произведений ЭДС в каждой ветви на проводимость ветви, присоединенной к рассматриваемому узлу. Произведение Eg записывается с положительным знаком, если ЭДС направлена к узлу, для которого записывается уравнение. Если в схеме есть источники тока J, то они входят в сумму в правых частях уравнений. Знак определяется тем же правилом.
|
|
|
6. Метод суперпозиции (наложения) и метод эквивалентного генератора В некоторых случаях бывает необходимо исследовать режим работы только одной ветви схемы, при этом целесообразно воспользоваться методом эквивалентного генератора. Воздействие всех источников сложной электрической цепи на исследуемую ветвь можно заменить воздействием последовательно соединенного эквивалентного генератора с ЭДС Еэкв и внутренним сопротивлением Rэкв. Эквивалентная ЭДС будет равна разности потенциалов на зажимах схемы при исключении данной ветви.
Эквивалентное
сопротивление равно сопротивлению
всей схемы при исключении из рассмотрения
данной ветви и равенстве нулю всех
источников тока и ЭДС. В итоге искомый
ток находится следующим образом:\
|
Принцип наложения (суперпозиции) Воздействие нескольких источников, на какой либо элемент цепи можно рассматривать как результат воздействия на этот элемент каждого из источников в отдельности независимо от других: то есть ток в любой ветви рассматривают как результат наложения токов, получающихся от отдельных источников, действующих независимо друг от друга.
|
|
|
7. Переменный синусоидальный ток, основные понятия, определения и способы прелставления синусоидальных ЭДС, напряжений и токов. Синусоидальные токи позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. В линейных электрических синусоидальные токи всегда сохраняют свою фазу. Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями и представить в виде вращающихся векторов на декартовой или комплексной плоскости.
Запишем синусоидальные напряжения с помощью тригонометрических функций:
|
Величина ω называется угловой частотой:
При совместном рассмотрении двух синусоидально изменяющихся величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз:
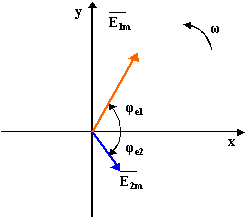
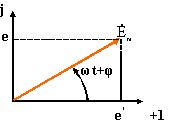
При изображении синусоидальных ЭДС, напряжений и токов вращающимися векторами на декартовой плоскости из начала координат проводят векторы, равные амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки с угловой скоростью ω. Фазовый угол отсчитывают от положительной оси абсцисс.
|
|
|
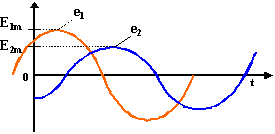
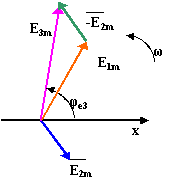
Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты, называют векторными диаграммами. При построении векторных диаграмм часто удобно принимать t=0. При этом сложение и вычитание синусоидально изменяющихся величин можно заменить сложением и вычитанием их векторов:
Результирующие напряжение также будет синусоидальным.
|
|
|
|
|
|
|
|
|
|
|
|
8. Символическое представление переменного синусоидального тока.
Пусть
мгновенная ЭДС задаётся уравнением:
На
комплексной плоскости вращающийся
вектор:
Мгновенная
фаза:
Мнимая
составляющая комплексного числа
вектора на комплексной плоскости
определяет синусоидальное изменение
ЭДС и обозначается символом Im.
Комплексное
число
|
Комплексное число Ėm, соответствующее положению вектора в начальный момент времени называют комплексной амплитудой:
Комплексное
число ej∙ω∙t
является оператором поворота вектора
на угол ω∙t относительно начального
положения вектора. Следовательно,
мгновенное значение синусоидальной
величины равно мнимой части без знака
? произведения комплекса амплитуды
Ėm
и оператора вращения ej∙ω∙t
:
Переход от одной формы записи, к другой, осуществляется с помощью формулы Эйлера:
Применение комплексных чисел позволяет от геометрического сложения или вычитания векторов на векторной диаграмме перейти к алгебраическому действию над комплексными числами этих векторов. Метод расчета цепей синусоидального тока, основанный на изображении гармонических функций времени комплексными числами, называется методом комплексных величин, методом комплексных амплитуд или комплексным методом расчета (впервые был предложен Ч.П. Штейнметцем). |
||||||||||||||||||||||||||||||||||||||||||||||||
|
9. Идеальные элементы электрической цепи синусоидального тока. Идеальный резистивный элемент
Резистивный
элемент характеризует необратимые
процессы преобразования электрической
энергии в другие виды энергии. Для
мгновенных значений тока через
резистивный элемент справедлив закон
Ома:
т.е.
кривые напряжения и тока резистивного
элемента подобны. Мгновенная мощность
резистивного элемента не зависит от
знака тока и всегда положительна: Идеальный индуктивный элемент
Индуктивный
элемент характеризует наличие
изменяющегося магнитного поля,
созданного изменяющимся током.
Индуктивный элемент с индуктивностью
L учитывает энергию магнитного поля
Падение
напряжения на индуктивности :
противоположно наведенной ЭДС. Условились положительное направление ЭДС самоиндукции брать совпадающим с положительным направлением тока, который наводит эту ЭДС.
|
Мгновенная
мощность индуктивного элемента: Идеальный ёмкостный элемент Ёмкостный элемент характеризует влияние изменяющегося электрического поля элементов цепи. Ёмкостный элемент с ёмкостью С учитывает энергию электрического поля:
Для ёмкостного элемента:
возрастают, т.е. энергия электрического тока передаётся электрическому полю, когда uc убывает, энергия электрического поля возвращается в электрическую цепь. Напряжение на ёмкости определяется:
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
10. Закон Ома для резистивного, индуктивного и емкостного элементов.
где z = U/I— модуль полного сопротивления; φ - угол сдвига фаз между током и напряжением. Выразив комплексное значение полного сопротивления в тригонометрической и затем в алгебраической форме, получим: для цепи с активно-индуктивным характером (рис. 2.24, в), ψ1 > ψ2, Z = zejφ = z cos φ + jz sin φ = r + jxL; для цепи с активно-емкостным характером (рис. 2.24, г), ψ2 > ψ1, Z = ze-jφ = z cos φ - jz sin φ = r - jxC, где r = z cos φ, xL = z sin φ, xC = z sin φ — соответственно активное, индуктивное и емкостное сопротивления цепи. Закон Ома в комплексной форме: I = U/Z, где Z = r + jxL для цепи, состоящей из последовательно включенных активного r и индуктивного xL сопротивлений; Z = r -- jxC для цепи, состоящей из последовательно включенных активного r и емкостного хC сопротивлений. Полная проводимость в комплексной форме записывается следующим образом: для цепи, состоящей из последовательно включенных активного и индуктивного сопротивлений,
для цепи, состоящей из последовательно включенных активного и емкостного сопротивлений,
где g и b— соответственно активная и реактивная проводимости цепи. |
11. Неразветвленная цепь синусоидального тока. Резонанс напряжений. Известно, что в механической системе резонанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. В общем случае под резонансом электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе, и, следовательно, эквивалентная схема цепи представляет собой активное сопротивление. Такое состояние цепи имеет место при определенном соотношении ее параметров r, L, С, когда резонансная частота цепи равна частоте приложенного к ней напряжения. Резонанс в электрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля индуктивности и наоборот. При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных ее участках. В цепи, где r, L, С соединены последовательно, может возникнуть резонанс напряжений, а в цепи, где r, L, С соединены параллельно,— резонанс токов. Полная мощность равна активной мощности; S = √P2 + Q2 = P, так как реактивная мощность равна нулю. Коэффициент мощности равен единице: cos φ = P/S = r/z = 1. Явления резонанса широко используются в радиоэлектронных устройствах и в заводских промышленных установках.
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
13. Резонанс токов. Разветвленная цепь синусоидального тока. Резонансом токов называется такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только активную мощность. , общий ток цепи совпадает по фазе с напряжением, если реактивные составляющие токов ветвей с индуктивностью и емкостью равны по модулю: I1р = I2р. Общий реактивный ток цепи, равный разности реактивных токов ветвей, в этом случае равен нулю: I1р - I2р = 0. Общий ток цепи имеет только активную составляющую, равную сумме активных составляющих токов ветвей: Iа = I1а + I2а . Выразив реактивные токи через напряжения и реактивные проводимости, получим UbL = UbС, откуда bL = bС. Итак, при резонансе токов реактивная проводимость ветви с индуктивностью равна реактивной проводимости ветви с емкостью. При резонансе токов коэффициент мощности равен единице: cos φ = 1. Полная мощность равна активной мощности: S = P. Реактивная мощность равна нулю: Q = QL - QC = 0. Реактивная энергия действует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода энергия электрического поля емкости переходит в энергию магнитного поля индуктивности. Обмена реактивной энергией между потребителями цепи и источником питания не происходит. Ток в проводах, соединяющих цепь с источником, обусловлен только активной мощностью. Большинство промышленных потребителей переменного тока имеют активноиндуктивный характер; некоторые из них работают с низким коэффициентом мощности и, следовательно, потребляют значительную реактивную мощность. К таким потребителям относятся асинхронные двигатели, особенно работающие с неполной нагрузкой, установки электрической сварки, высокочастотной закалки и т. д. Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов. |
14. Комплексный метод расчета. В практике расчета цепей переменного тока широко используются комплексные числа.Комплексными числами и векторами на комплексной плоскости изображаются изменяющиеся синусоидально ЭДС, ток и напряжение, а также полные сопротивление и проводимость, полная мощность и некоторые другие параметры цепи. Использование комплексных чисел при расчете электрических цепей переменного тока позволяет заменить графические действия над векторами алгебраическими действиями над комплексными числами. Кроме того, при использовании комплексных чисел возникает полная аналогия записей уравнений по законам Ома и Кирхгофа и методов расчета цепей переменного тока с цепями постоянного тока. В цепях постоянного тока в уравнения входят действительные значения Е, U, I, r, в цепях переменного тока — комплексные значения U, E, I, Z. Комплексная плоскость представляет собой прямоугольною систему координат. По одной оси. называемой действительной и обозначаемой ( + ), ( — ), откладывается действительная составляющая комплекса (a), по другой оси, называемой мнимой и обозначаемой (+j), (-j), — мнимая составляющая комплекса (b). Комплексное число обозначается чертой под буквенным обозначением. Комплексное число может быть представлено вектором, длина которого является модулем комплекса, а положение определяется углом α относительно положительной действительной оси комплексной плоскости (рис. 2.23, а). Выразив а и b через модуль (длину вектора) и угол, можно записать комплексное число в тригонометрической форме: С = а + jb = с cos α + jc sin α, где с = √а2 + b2 — модуль комплексного числа
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|

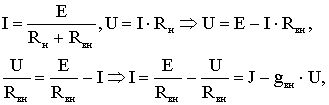

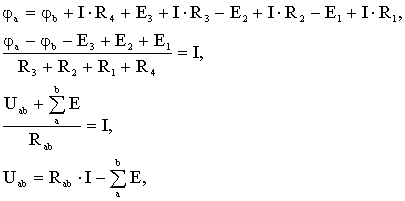
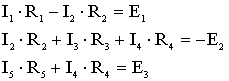
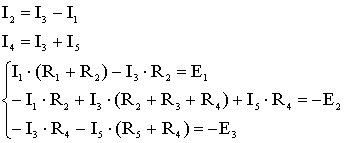
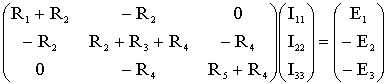

 Подставляем
в уравнения, полученные по первому
закону Кирхгофа
Подставляем
в уравнения, полученные по первому
закону Кирхгофа