1. Определители. Свойства. Вычисление. Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определительматрицыявляетсямногочленомот элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случаематрицаможет быть определена над любым коммутативнымкольцом, в этом случае определитель будет элементом того же кольца. ОпределительматрицыА обозначается как: det(A), |А| или Δ(A). Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): , гдеи т. д. — строчки матрицы,— определитель такой матрицы.

При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

-Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

-Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

-Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

-Общий множитель элементов какого-либо ряда определителя можно вынести зазнак определителя.

-Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

-Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

-Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

-Определитель произведения квадратных матриц одинакового порядка равепроизведению их определителей (cм. также формулу Бине-Коши).

-С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:

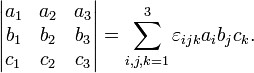
2. Решение систем линейных уравнений методом Крамера

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравненийс ненулевымопределителемосновной матрицы(причём для таких уравнений решение существует и единственно). Назван по имениГабриэля Крамера(1704–1752), придумавшего метод.

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

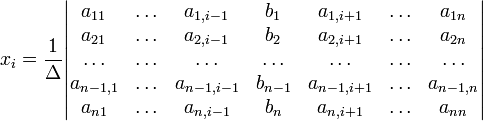
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Система линейных уравнений:

Определители:

Решение:

Пример:

Определители:

Метод Крамера требует вычисления n+ 1 определителей размерности. При использованииметода Гауссадля вычисления определителей, метод имеет временную сложность порядкаO(n⁴), что хуже, чем если быметод Гауссанапрямую использовался для решения системы уравнений. Поэтому метод считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностьюO(n³), сравнимой со сложностьюметода Гаусса.^[1]

3. Решение систем линейных уравнений методом Гаусса. Ме́тод Га́усса^[1]— классический метод решениясистемы линейных алгебраических уравнений(СЛАУ). Это метод последовательного исключенияпеременных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные Пусть исходная система выглядит следующим образом

Матрица Aназывается основной матрицей системы,b— столбцом свободных членов.

Тогда согласно свойству элементарных преобразованийнад строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор(ненулевойминормаксимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных^[3].

Тогда переменные называютсяглавными переменными. Все остальные называютсясвободными.

Если хотя бы одно число , гдеi>r, то рассматриваемая система несовместна.

Пусть для любыхi>r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом (, где— номер строки):

, где

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путёмэлементарных преобразованийнад исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

Алгоритм решения СЛАУметодом Гаусса подразделяется на два этапа.

• На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразованийнад строками систему приводят к ступенчатой илитреугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.

• На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.

Метод Гаусса требует порядка O(n³) действий.

Достоинства метода:  Менее трудоёмкий по сравнению с другими методами.

 Позволяет однозначно установить, совместна система или нет, и если совместна, найти её решение.

 Позволяет найти максимальное число линейно независимых уравнений — ранг матрицы системы

4. Матрицы. Действия над матрицами. Свойства матриц.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.

Матрицы допускают следующие алгебраические операции:

• сложение матриц, имеющих один и тот же размер;

• умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно умножить справа на матрицу, имеющую n строк);

• умножение матрицы на элемент основного кольца или поля (т. е. скаляр).

Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Прямоугольной матрицей размера m´n называется совокупность mn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде

                   

Числа a_{i j}, составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы A = (a_{i j}) и B = (b_{i j}) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a_{i j} = b_{i j}.Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера m´n, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами.

5. Обратная Матрица.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы:

• , где обозначаетопределитель.

• для любых двух обратимых матриц A и B.

• где * ^T обозначает транспонированную матрицу.

• для любого коэффициента .

• Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1} существует, то x = A ^{− 1}b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

6. Решение систем линейных уравнений матричным методом.

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме:

AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A ^{− 1} — матрицу, обратную к матрице A:

Так как A ^{− 1}A = E, получаем X = A ^{− 1}B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

.

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

[править] Пример решения неоднородной СЛАУ

Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.

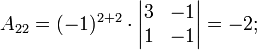
Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.

Подставляя переменные в формулу, получаем:

Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.

Итак, x=2; y=1; z=4.

7. Векторы. Линейные операции над векторами.

8. Скалярное произведение двух векторов. Скаля́рное произведе́ние— операция над двумявекторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножениедлиныданного вектора x напроекциюдругого вектора y на данный вектор x. Эта операция обычно рассматривается каккоммутативнаяилинейнаяпо каждому сомножителю.

Обычно используется одно из следующих обозначений:

,

,

,

или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):

.

Обычно предполагается что скалярное произведение положительно определено, то есть

для всех .

9. Векторное произведение двух векторов.

Векторным произведениемвекторана векторв пространственазывается вектор, удовлетворяющий следующим требованиям:

• длина вектора равна произведению длин векторовинасинусугла; между ними

• вектор ортогоналенкаждому из векторови

• вектор направлен так, что тройка векторовявляется правой.

• в случае пространства требуется ассоциативность тройки векторов.

Обозначение:

В литературе^[1]определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левойпрямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.

Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.

10. Смешанное произведение трёх векторов. Тройкой векторов называются три вектора, если указано, какой из них считается первым, какой вторым и какой третьим. Тройку векторов записывают в порядке нумерации; например, запись ,,означает, что вектор считается первым,- вторым,- третьим.

Тройка некомпланарных векторов ,,называется правой, если составляющие ее векторы, будучи приведены к общему началу, располагаются в порядке нумерации аналогично тому, как расположены большой, указательный и средний пальцы правой руки. Если векторы ,,расположены аналогично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой.

Смешанным произведенем трех векторов ,,называется число, равное векторному произведению , умноженному скалярно на вектор, то есть.

Имеет место тождество, ввиду чего для обозначения смешанного произведенияупотребляется более простой символ. Таким образом,

,.

Смешанное произведение равно объему параллелепипеда, построенного на векторах,,, взятого со знаком плюс, если тройка правая, и со знаком минус, если эта тройка левая. Если векторы,,компланарны (и только в этом случае), смешанное произведение равно нулю; иначе говоря, равенство

есть необходимое и достаточное условие компланарности векторов ,,.

Если векторы ,,заданы своими координатами:

,,,

то смешанное произведение определяется формулой

.

Напомним, что система координатных осей предполагется правой (вместе с тем является правой и тройка векторов ,,).

11. Прикладные задачи векторного анализа: Объем параллелепипеда

объем параллелепипеда

     Если параллелепипед построен на приведенных к общему началу векторах , а,,,- радиус-векторы его соответствующих вершинто объем параллелепипеда

     В координатах

12. Прикладные задачи векторного анализа: Площадь тетраэдра. 13. Прикладные задачи векторного анализа: Площадь треугольника

14. Прикладные задачи векторного анализа: Площадь параллелограмма По определению векторного произведения двух векторов модуль векторного произведения равен площади параллелограмма, построенного на этих векторах. Поэтому для решения задачи найдем сначала векторное произведение, а потом его модуль. Согласно

имеем

а модуль

Искомая площадь параллелограмма

S= 19,26 кв. ед.

Замечание.

Векторное произведение можно было сразу определить по формуле

в которой следует взять

a_x= 5;a_y= -4;a_z= 7;

b_x= 1;b_y= 1;b_z= -2.

15. Прямая на плоскости. Угол между двумя прямыми. Прямая— одно из основных понятийгеометрии.

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомамигеометрии.

Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.

Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

16. Уравнение прямой. Общее уравнение прямойлинии на плоскости вдекартовых координатах:

где A,BиC— произвольные постоянные, причем постоянныеAиBне равны нулю одновременно.Векторс координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C= 0 прямая проходит черезначало координат. Также уравнение можно переписать в виде :

17. Кривые второго порядка.

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов отличен от нуля.

Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты и корни характеристического уравнения(см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).

Вид кривой	Каноническое уравнение	Инварианты
Невырожденные кривые()
Эллипс
Гипербола
Парабола
Вырожденные кривые(Δ = 0)
Точка
Две пересекающиеся прямые
Две параллельные прямые
Одна прямая	x2= 0

Для центральной кривой в каноническом виде её центр находится в начале координат.

18. Общее уравнение кривых второго порядка.

Общее уравнение кривой можно записать в матричном виде