
Материал на экзамен
.pdfТеория множеств
Определение и понятие
В основе теории множеств лежат первичные понятия: множество и отношение принадлежности множества (обозначается как  — «
— «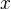 есть элемент множества
есть элемент множества  », «
», « принадлежит множеству
принадлежит множеству  »). Пустое множество, обычно обозначается символом
»). Пустое множество, обычно обозначается символом  — множество, не содержащее ни одного элемента. Подмножество и надмножество — соотношения включения одного множества в другое (обозначаются соответственно
— множество, не содержащее ни одного элемента. Подмножество и надмножество — соотношения включения одного множества в другое (обозначаются соответственно  и
и  для нестрогого включения и
для нестрогого включения и  и
и  — для строгого).
— для строгого).
Частично упорядоченное множество — математическое понятие, которое формализует интуитивные идеи упорядочения, расположения элементов в определенной последовательности. Неформально, множество частично упорядочено, если указано, какие элементы следуют за какими (какие элементы больше каких). В общем случае может оказаться так, что некоторые пары элементов не связаны отношением «следует за».
В качестве абстрактного примера можно привести совокупность под-
множеств множества из трех элементов  (булеан данного множества), упорядоченную по отношению включения.
(булеан данного множества), упорядоченную по отношению включения.
Отношение частичного порядка обычно обозначают символом  , по аналогии с отношением «меньше либо равно» на множестве действи-
, по аналогии с отношением «меньше либо равно» на множестве действи-
тельных чисел. При этом, если  , то говорят, что элемент
, то говорят, что элемент  не превосходит
не превосходит  , или что
, или что  подчинен
подчинен  .
.
Если  и
и  , то пишут
, то пишут  , и говорят, что
, и говорят, что  меньше
меньше  , или что
, или что  строго подчинен
строго подчинен  .
.
Иногда, чтобы отличить произвольный порядок на некотором множе-

стве от известного отношения «меньше либо равно» на множестве действительных чисел, вместо  и
и  используют специальные символы
используют специальные символы  и
и  соответственно.
соответственно.
Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным. Например,
конечное множество из пяти элементов. Число элементов конечного множества это натуральное число и называется мощностью множества. Множество всех положительных целых чисел бесконечно:
Бесконечное множество — множество, не являющееся конечным. Можно дать ещё несколько эквивалентных определений бесконечного множества:
•Множество, в котором для любого натурального числа  найдётся конечное подмножество из
найдётся конечное подмножество из  элементов.
элементов.
•Множество, в котором найдётся счётное подмножество.
•Множество, в котором найдётся подмножество, равномощное некоторому (ненулевому) предельному ординалу.
•Множество, для которого существует биекция с некоторыми его собственными подмножествами.
Для любого бесконечного множества существует множество с ещё большей мощностью — таким образом, не существует бесконечного множества наибольшей мощности. Мощности бесконечных множеств
называются алефами и обозначаются  где индекс
где индекс  пробегает все порядковые числа. Мощности бесконечных множеств составляют вполне упорядоченный класс — наименьшей мощностью бесконеч-
пробегает все порядковые числа. Мощности бесконечных множеств составляют вполне упорядоченный класс — наименьшей мощностью бесконеч-

ного множества является |
(алеф-0, мощность множества натураль- |
|||
ных |
чисел), |
за |
ним |
следуют |
Над множествами определены следующие операции:
•объединение, обозначается как  — множество, содержащее все элементы из
— множество, содержащее все элементы из  и
и 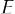 ,
,
•разность, обозначается как  , реже
, реже  — множество элементов
— множество элементов  , не входящих в
, не входящих в  ,
,
•дополнение, обозначается как  или
или  — множество всех элементов, не входящих в
— множество всех элементов, не входящих в  (в системах, использующих универсальное множество),
(в системах, использующих универсальное множество),
•пересечение, обозначается как  — множество из элементов, содержащихся как в
— множество из элементов, содержащихся как в  , так и в
, так и в  ,
,
•симметрическая разность, обозначается как  , реже
, реже
 — множество элементов, входящих только в одно из множеств —
— множество элементов, входящих только в одно из множеств —  или
или  .
.
Объединение и пересечение также часто рассматривают над семей-
ствами множеств, обозначаются  и
и  и составляют, соответственно, объединение всех множеств, входящих в семейство
и составляют, соответственно, объединение всех множеств, входящих в семейство  и пересечение всех множеств, входящих в семейство.
и пересечение всех множеств, входящих в семейство.
Объединение и пересечение коммутативны, ассоциативны и идемпотентны. В зависимости от выбора системы аксиом и наличия дополнения алгебра множеств (относительно объединения и пересечения) может образовывать дистрибутивную решётку, полную дистрибутивную решётку, булеву алгебру. Для визуализации операций над множествами использу-

ются диаграммы Венна. |
|
|
|
|
|
Декартово произведение множеств |
и — множество всех упо- |
||||
рядоченных |
пар |
элементов |
из |
и |
: |
|
|
|
Отображение |
множества |
|
в множество |
теории множеств рассматривается как бинарное от- |
||||
ношение — подмножество |
— с условием единственности со- |
||||
ответствия |
первого |
элемента |
|
второму: |
|
 .
.
Булеан — множество всех подмножеств данного множества, обозначается  или
или 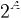 (так как соответствует множеству отображений из
(так как соответствует множеству отображений из  в
в 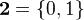 ).
).
Мощность множества (кардинальное число) — характеристика количества элементов множества, формально определяется как класс эквивалентности над множествами, между которыми можно установить
взаимно-однозначное соответствие, обозначается  или
или  . Мощность пустого множества равна нулю, для конечных множеств — целое число, равное количеству элементов. Над кардинальными числами, в том числе характеризующими бесконечные множества, можно установить отношение порядка, мощность счётного множества обозначается
. Мощность пустого множества равна нулю, для конечных множеств — целое число, равное количеству элементов. Над кардинальными числами, в том числе характеризующими бесконечные множества, можно установить отношение порядка, мощность счётного множества обозначается 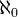 (алеф — первая буква еврейского алфавита), является наименьшей из мощностей бесконечных множеств, мощность конти-
(алеф — первая буква еврейского алфавита), является наименьшей из мощностей бесконечных множеств, мощность конти-
нуума обозначается  или
или  , континуум-гипотеза — предположение о том, что между счётной мощностью и мощностью континуума нет промежуточных мощностей.
, континуум-гипотеза — предположение о том, что между счётной мощностью и мощностью континуума нет промежуточных мощностей.
Декартово произведение
Прямое или декартово произведение двух множеств — это множество, элементами которого являются всевозможные упорядоченные пары элементов исходных множеств.

Понятие прямого произведения естественно обобщается на произведение множеств с дополнительной структурой (алгебраической, топологической и т. д.), поскольку произведение множеств часто наследует структуры, имевшиеся на исходных множествах.
Произведение двух множеств
Пусть даны два множества  и
и  . Прямое произведение множества
. Прямое произведение множества  и множества
и множества  есть такое множество
есть такое множество  , элементами кото-
, элементами кото-
рого являются упорядоченные пары  для всевозможных
для всевозможных  и
и  .
.
Отображения произведения множеств в его множители —  и
и
 — называют координатными функциями.
— называют координатными функциями.
Аналогично определяется произведение конечного семейства множеств.
Строго |
говоря, |
тождество |
ассоциативности |
 не имеет места, но в силу существования естественного взаимно однозначного соответствия между
не имеет места, но в силу существования естественного взаимно однозначного соответствия между
множествами 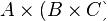 и
и  этим различием можно зачастую пренебречь.
этим различием можно зачастую пренебречь.
Декартова степень
 -я Декартова степень множества
-я Декартова степень множества  определяется для целых неотрицательных
определяется для целых неотрицательных  , как
, как  -кратное Декартово произведение
-кратное Декартово произведение  на себя:
на себя:

Обычно обозначается как  или
или  .
.
При положительных  Декартова степень
Декартова степень  состоит из всех упорядоченных наборов элементов из
состоит из всех упорядоченных наборов элементов из  длины
длины  . Так вещественное
. Так вещественное
пространство  (множество кортежей из трех вещественных чисел), есть 3 степень множества вещественных чисел
(множество кортежей из трех вещественных чисел), есть 3 степень множества вещественных чисел 
При  , Декартова степень
, Декартова степень  по определению, содержит единственный элемент — пустой кортеж.
по определению, содержит единственный элемент — пустой кортеж.
Прямое произведение семейства множеств
В общем случае, для произвольного семейства множеств (не обязательно различных)  (множество индексов может быть бес-
(множество индексов может быть бес-
конечным) прямое |
произведение |
определяется как |
множество функций, сопоставляющих каждому элементу |
||
элемент множества |
: |
|
Отображения  называются проекциями.
называются проекциями.
В частности, для конечного семейства множеств  лю-
лю-
бая функция  с условием
с условием  эквивалентна некоторому кортежу длины
эквивалентна некоторому кортежу длины  , составленному из элемен-
, составленному из элемен-
тов множеств  , так, что на
, так, что на  -ом месте кортежа стоит элемент множества
-ом месте кортежа стоит элемент множества  . Поэтому декартово (прямое) произведение конечного
. Поэтому декартово (прямое) произведение конечного
числа множеств  может быть записано так:
может быть записано так:

Проекции определяются следующим образом: 
Симметрическая разность двух множеств — теоретико-множествен- ная операция, результатом которой является новое множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. Другими словами, если есть два множества  и
и  , их симметрическая разность есть объединение элементов
, их симметрическая разность есть объединение элементов  , не входящих в
, не входящих в  , с элементами
, с элементами  не входящими в
не входящими в 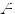 . На письме для обозначения симметрической разности множеств
. На письме для обозначения симметрической разности множеств  и
и  используется обозначение
используется обозначение  так же, реже используется обозначение:
так же, реже используется обозначение: 
Симметрическую разность можно ввести двумя способами:
•симметрическая разность двух заданных множеств  и
и  — это такое множество
— это такое множество  , куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество:
, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество:
•симметрическая разность двух заданных множеств  и
и  — это такое множество
— это такое множество  , куда входят все те элементы обоих множеств, которые не являются общими для двух заданных множеств.
, куда входят все те элементы обоих множеств, которые не являются общими для двух заданных множеств.
Понятие симметрической разности можно обобщить на число множеств, большее двух.
Симметрическая разница является бинарной операцией на любом булеане;
• Симметрическая разность коммутативна:

•Симметрическая разность ассоциативна:
•Пересечение множеств дистрибутивно относительно симметрической разности:
•Пустое множество является нейтральным элементом симметрической разности:
•Любое множество обратно само себе относительно операции симметрической разности:
•В частности, булеан с операцией симметрической разности является абелевой группой;
•Булеан с операцией симметрической разности также является векторным пространством над полем 
•В частности, булеан с операциями пересечения множеств и симметрической разности является алгеброй с единицей.
•
•
•
•Если роль «суммы» играет операция симметрической разности, а роль «произведения» — пересечение множеств, то множества образуют кольцо без единицы. Причем другие основные опера-

ции теории множеств, разность и объединение, можно выразить через них:
•Объединение симметрической разности с пересечением двух множеств равно объединению исходных множеств
Пусть
Тогда
Соответствием между множествами X и Y называется всякое подмножество декартова произведения этих множеств. Соответствия принято обозначать буквами P, S, T и др. Если xSy — соответствие между элементами множеств X и Y, то, согласно определению, S X
X Y.
Y.
Поскольку соответствие — это подмножество, то его можно задать как любое множество, т. е. либо перечислив все пары элементов, находящихся в данном соответствии, либо указав характеристическое свойство элементов этого подмножества. Например, соответствие между множествами X={1, 2, 4, 6} и Y={3, 5} можно задать: 1) при помощи предложения с двумя переменными: a<b при условии, что a X, b
X, b Y;
Y;
2) перечислив пары чисел, принадлежащих подмножеству декартова произведения X Y: {(1, 3),(1, 5), (2, 3), (2, 5), (4, 5)}.
Y: {(1, 3),(1, 5), (2, 3), (2, 5), (4, 5)}.
Отображение множеств.
Пусть X и Y — два произвольных множества.
Определение. Соответствие, при котором каждому из элементов множества X сопоставляется единственный элемент из множества Y, называется отображением.
Обозначение отображения из множества X в множество Y: X fY.
Множество X называется областью определения отображения и обозначается X=D(f).
E(f) называется множеством значений отображения, и E(f)={y Y|
x X,y=f(x)}.
Множество Γ(f) называется графиком отображения.
Γ(f)={(x,y) X×Y,y=f(x), x X,y Y}.
Пусть f — некоторое отображение из множества X в множество Y. Если x при этом отображении сопоставляется y, то y=f(x). При этом y называется образом x, или значением отображения f в точке x. А x, соответственно, прообразом элемента y.
Исходя из определения отображения, видно, что не требуется, чтобы все элементы в множестве Y являлись образами какого-либо x и при том единственного.
Пример.
Даны два множества X={с,е,н,т,я,б,р,ь} и Y={1,2,3,4,5,9,10,11}
Отображение из множества X в множество Y имеет следующий вид:
{ |
с, |
е, |
н, |
т, |
я, |
б, |
р, |
ь |
} |
|
↕ |
↕ ↕ ↕ ↕ ↕ ↕ |
↕ |
|
|||||
{ |
1, |
2, |
3, |
4, |
5, |
9, |
10, 11 |
} |
|
