Дискретная математика. Методичка. Кацаран

Федеральное агентство по образованию Государственное образовательное учреждение Высшего профессионального образования

МНОЖЕСТВА. БИНАРНЫЕ ОТНОШЕНИЯ. КОМБИНАТОРИКА Методическое пособие для вузов

Для студентов 1 курса дневного и вечернего отделений факультета прикладной математики, информатики и механики

Составители: Т.К. Кацаран Л.Н. Строева

Издательско-полиграфический центр Воронежского государственного университета

2007

Курс дискретной математики представляет собой объединение следующих взаимосвязанных разделов: множества, отношения, комбинаторика, математическая логика, булевы функции и их приложения, алгоритмы, графы и их применение, кодирование.

Согласно учебному плану по специальности Прикладная математика и информатика более четверти объема информации по данному курсу рекомендуется для самостоятельного изучения. В связи с этим и по причине отсутствия доступной литературы по некоторым разделам курса авторами подготовлено данное методическое пособие.

Методическое пособие содержит краткий курс лекций по дисциплине Дискретная математика , читаемому на факультете ПММ для студентов 1 курса дневного и вечернего отделений, программу курсаДискретная математика и состоит из четырех глав, в которых изложены основные понятия (определения) и факты (утверждения, свойства, теоремы и их следствия) по темам Множества , Бинарные отношения , Комбинаторика , Линейные рекуррентные соотношения второго порядка . Особое внимание уделено доказательствам теорем, так как они содержат в себе методику исследования и решения теоретических и практических задач разного уровня, приведенных в конце каждой из глав.

ПРОГРАММА КУРСА ДИСКРЕТНАЯ МАТЕМАТИКА

I. Множества и отношения. Канторовское описание множества. Способы задания множеств. Операции над множествами и их свойства. Мощность конечного множества. Булеан множества, прямое произведение двух и более множеств, степень множества, вычисление мощности конечного множества.

Определение и способы задания отношений. Операции над отношениями. Свойства бинарных отношений. Отношение эквивалентности и разбиение множества на классы, их взаимосвязь. Отношения строгого и нестрогого порядка. Частично и вполне упорядоченные множества.

II. Комбинаторика. Правило суммы и правило произведения. Понятие k-выборки. Размещения, перестановки, сочетания. Бином Ньютона. Свойства сочетаний.

Формула включений и исключений и ее применение.

III. Линейные рекуррентные соотношения (ЛРС) второго порядка. Общее и частное решение ЛРС в случае простых и кратных корней характеристического уравнения. Уравнение и числа Фибоначчи.

IV. Математическая логика. Высказывания. Операции над вы-

3

сказываниями и их свойства. Формулы алгебры высказываний. Равносильность формул. Дизъюнктивная и конъюнктивная нормальные формы. Основные правила теории доказательств.

V. Предикаты. Определение предикатов и способы их задания. Операции над предикатами. Формулы логики предикатов. Равносильность формул. Кванторы общности и существования n-местных и одноместных предикатов и их свойства.

Теоретико-множественный смысл предикатов. Приведенная и предваренная нормальные формы.

VI. Булевы функции и их приложения. Определение и способы задания булевых функций от n переменных. Элементарные булевы функции. Принцип двойственности и его применение.

Специальные виды формул. Совершенные дизъюнктивная и конъюнктивная нормальные формы. Полином Жегалкина.

Операция замыкания и ее свойства. Основные замкнутые классы. Леммы о несамодвойственной, немонотонной и нелинейной функциях.

Замкнутость и полнота. Теорема о полноте двух систем. Теорема о функциональной полноте, ее значение и практическое применение.

Применение булевых функций к синтезу и анализу дискретных устройств. Синтез сумматора.

Задача минимизации дизъюнктивных нормальных форм (ДНФ). Минимальная и кратчайшая ДНФ. Сокращенная ДНФ и способы ее построения. Тупиковая ДНФ.

VII. Алгоритмы. Интуитивное описание алгоритма и его свойства. Машина Тьюринга. Функции, вычислимые по Тьюрингу.

Кодирование машины Тьюринга. Самоприменимые и несамоприменимые машины Тьюринга. Алгоритмически неразрешимые проблемы.

Вычислимые функции. Правила подстановки, примитивной рекурсии и взятия µ -оператора. Функции примитивно-рекурсивные, общерекурсивные и частично-рекурсивные.

VIII. Графы и их применение. Основные понятия теории графов. Отношение связности на множестве вершин графа. Компоненты связности графа. Связные графы.

Деревья. Характеристическое свойство дерева. Остов графа. Теорема о соотношении числа вершин и ребер в дереве.

Эйлеровы графы. Необходимое и достаточное условие эйлеровости графа. Задача о кенигсбергских мостах.

Операции над подграфами. Цикломатическое число графа. Теоремы о размерности подпространства всех четных подграфов связного графа и графа с n компонентами связности.

4

Задача о раскраске географической карты. Правильно раскрашенный граф. Хроматическое число графа и хроматический класс графа. Бихроматические графы. Необходимое и достаточное условие бихроматичности графа.

Внутренне устойчивое и внешне устойчивое множества. Числа внутренней и внешней устойчивости графа. Ядро графа.

Транспортные сети. Основная задача теории транспортных сетей. Алгоритм Форда-Фалкерсона построения потока максимальной величины. Обоснование алгоритма Форда-Фалкерсона.

IX. Кодирование. Постановка основных задач теории кодирования. Алфавитное и равномерное кодирование. Критерий однозначности декодирования. Самокорректирующиеся коды. Коды Хемминга.

Кодовое дерево. Методы кодирования для ансамбля сообщений. Метод Шеннона-Фано и Хаффмэна.

5

ГЛАВА 1. МНОЖЕСТВА

§1. Определение и способы задания множеств

Множество это любое собрание вполне определенных и различимых объектов нашей интуиции или интеллекта, мыслимое как единое целое, это описание множества принадлежит основателю теории множеств Георгу Кантору (1845 1918).

Объекты, из которых состоит множество, называются его элементами. Множества будем обозначать прописными буквами латинского алфавита (A, B, C, X, Y, Z, . . .) , а элементы множеств строчными (x, y, z, a, b, c, . . .) . Зафиксируем следующие обозначения для наиболее важных числовых множеств: N множество натуральных чисел, Z множество целых чисел, R множество действительных чисел.

Множество A называется подмножеством множества B (обозначается A B , знак называется знаком включения),если каждый элемент множества A является элементом множества B .

Множества A и B равны ( A = B ), если одновременно имеют место включения A B и B A . Принадлежность элемента x множеству A обозначается x A , непринадлежность элемента x множеству A обозначается x / A .

Множество, не содержащее элементов, называется пустым и обозначается .

Множество, включающее элементы всех рассматриваемых в конкретной ситуации множеств, называется универсальным для данной

ситуации и обозначается U . Для любого множества имеют место включения: A U .

Рассмотрим способы задания множеств. Множество может быть задано: а) описанием характеристического свойства его элементов, б) при помощи списка или перечисления элементов множества, в) при помощи порождающей процедуры и т. д.

При задании множества A при помощи его характеристического свойства P (x) пишут A = {x| P (x)}.

При помощи списка могут задаваться только конечные множества, т. е. множества, состоящие из конечного числа элементов.

Порождающая процедура описывает способ получения элементов множества из уже полученных элементов или других объектов. Весьма распространенной порождающей процедурой является образование множеств из других множеств при помощи операций, которые рассмотрим ниже.

6

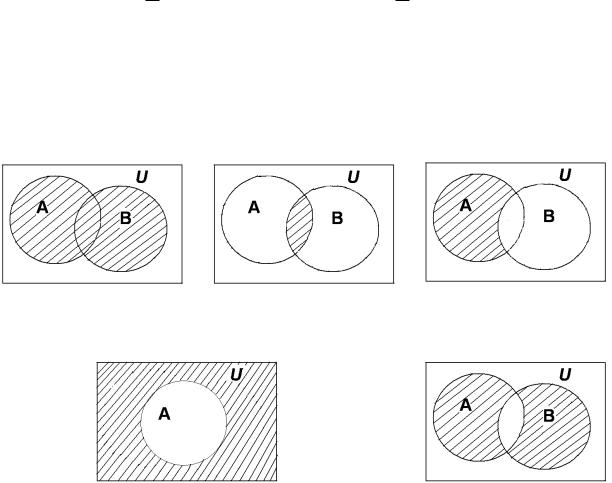
§ 2. Операции над множествами и их свойства

Объединением множеств A и B называется множество A B , состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств A или B :

A B = {x | x A или x B}.

Пересечением множеств A и B называется множество A ∩ B , состоящее из тех и только тех элементов, которые принадлежат одновременно множествам A и B :

A ∩ B = {x | x A и x B}.

Разностью множеств A и B называется множество A \ B тех и только тех элементов из A , которые не принадлежат множеству

B :

A \ B = {x | x A и x / B}.

Дополнение A определяется равенством A = U \ A , где U универсальное множество.

Симметричной разностью множеств A и B называется множество: A4B = (A \ B) (B \ A) .

Эти операции можно наглядно проиллюстрировать следующим образом:

Приведенные здесь рисунки называются диаграммами Эйлера-Венна.

7

Операции над множествами обладают следующими свойствами:

1)A = A (закон двойного отрицания);

2)A B = B A (коммутативность объединения);

3)A ∩ B = B ∩ A (коммутативность пересечения);

4)A (B C) = (A B) C (ассоциативность объединения);

5)A ∩ (B ∩ C) = (A ∩ B) ∩ C (ассоциативность пересечения);

6)A ∩ (B C) = (A ∩ B) (A ∩ C) (1-й дистрибутивный закон);

7)A (B ∩ C) = (A B) ∩ (A C) (2-й дистрибутивный закон);

8)A B = A ∩ B (закон де Моргана);

9)A ∩ B = A B (закон де Моргана);

10)A (A ∩ B) = A (закон поглощения);

11)A ∩ (A B) = A (закон поглощения);

12)A = A ;

13)A ∩ = ;

14)A U = U ;

15)A ∩ U = A .

§ 3. Мощность конечного множества

Число элементов конечного множества A называется его мощностью и обозначается |A|.

Говорят, что между множествами A и B установлено взаимооднозначное соответствие, если задан закон, по которому каждому элементу множества A соответствует один и тот же элемент множества B .

Между конечным непустым множеством A мощности n и отрезком натурального ряда {1, 2, . . . , n} существует взаимооднозначное соответствие.

Приведем очевидные свойства мощности конечных множеств:

1)| | = 0 ;

2)из A B следует |A| ≤ |B|, если при этом A 6= B , то |A| < |B|, следует отметить, что обратное утверждение не верно;

3)|A4B| ≤ |A| + |B|;

4)|A ∩ B| ≤ min{|A|, |B|};

5)|A B| = |A| + |B| − |A ∩ B|;

6)|A \ B| ≤ |A|;

7)|A4B| = |A B| − |A ∩ B|.

8

§ 4. Прямое произведение двух и более множеств

Прямым произведением двух множеств A = {a1, . . . , am} и

B = {b1, . . . , bn} называется множество A × B упорядоченных пар вида (ai, bj ) , где i = 1, m , j = 1, n .

Прямым произведением k множеств A1 , A2 , . . . , Ak называется

множество A1 ×A2 ×. . . ×Ak упорядоченных наборов (xi1 , xi2 , . . . , xik ) , длины k , где xi1 A1 , xi2 A2 , . . . , xik Ak .

Эти определения кратко можно записать так:

A × B = {(a, b) | a A, b B}.

A1 × A2 × . . . × Ak = {(xi1 , xi2 , . . . , xik ) | xi1 A1, xi2 A2, . . . , xik Ak }.

Теорема о мощности прямого произведения. Мощность прямого произведения конечного числа конечных множеств равна произведению мощностей этих множеств

|A1 × A2 × . . . × Ak | = |A1| · |A2| · . . . · |Ak |, k N.

Доказательство. Рассмотрим вначале случай двух множеств и докажем формулу |A × B| = |A| · |B|.

Пусть A = {a1, . . . , am} и B = {b1, . . . , bn}, тогда элементы A × B множества можно расположить в виде следующей таблицы:

которая содержит m строк и n столбцов. Поэтому число записанных в таблице упорядоченных пар равно mn = |A| · |B|.

Для доказательства теоремы в случае произвольного k воспользуемся методом математической индукции. При k = 1 теорема, очевидно, имеет место. Предположим, что она выполняется для случая (k − 1) -го множества и докажем ее для случая k множеств. С этой целью установим взаимооднозначное соответствие между множествами:

A1 × A2 × . . . × Ak и (A1 × A2 × . . . × Ak−1) × Ak

по правилу: элементу (ai1 , . . . , aik ) (A1 × A2 × . . . × Ak ) поставим в соответствие элемент ((ai1 , . . . , aik−1 ), aik ) (A1 × . . . × Ak−1) × Ak и наоборот. В силу взаимооднозначного соответствия между множествами

A1 × A2 × . . . × Ak и ((A1 × A2 × . . . × Ak−1) × Ak )

9

их мощности совпадают; используя утверждение теоремы для случая двух множеств, получаем:

|A1×A2×. . .×Ak | = |(A1×A2×. . .×Ak−1)×Ak | = |A1×A2×. . .×Ak−1||Ak |.

В силу предположения индукции |A1 × . . . × Ak−1| = |A1| . . . |Ak−1|, что завершает доказательство теоремы.

k

жества A . Из теоремы о мощности прямого произведения следует:

|Ak | = |A|k .

Пусть E = {0, 1}, тогда En = {(αi1 , . . . , αin )|αis {0, 1}, s = 1, . . . , n}, откуда следует |En| = |E|n = 2n , т. е. мощность множества всех наборов

длины n из нулей и единиц равна 2n .

§ 5. Булеан множества

Булеаном Б(A) множества A называется множество всех подмножеств этого множества: Б(A) = {X|X A}, если A = {a1, . . . , an}, то Б(A) = { , {a1}, . . . , {an}, . . . , {ai1 , . . . , ais }, . . .}.

Теорема о мощности булеана. Пусть A конечное множество мощности n , тогда мощность его булеана равна 2n : |Б(A)| = 2n .

Доказательство. Установим соответствие между множествами Б(A) и En по правилу: подмножеству {ai1 , . . . , ais } Б(A) поставим в соответствие набор длины n из нулей и единиц, в котором на местах с номерами i1, . . . , is стоят единицы, а на остальных местах нули. Это соответствие является взаимооднозначным, поэтому |Б(A)| = |En| = 2n . Теорема доказана.

В качестве примера приведенного в доказательстве теоремы соответствия рассмотрим случай n = 3 . Пусть A = {α, β, γ}, тогда

Б(A) = { , {α}, {β}, {γ}, {α, β}, {α, γ}, {β, γ}, {α, β, γ}};

E3 = {(0, 0, 0), (1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 1, 0), (1, 0, 1), (0, 1, 1), (1, 1, 1)}. Соответствие между E3 и Б(A) может быть установлено 8! различными способами (оно равно числу перестановок из элементов множества E3 ). В данном случае элементы множества E3 записаны так, что элементу, стоящему на k -ом месте, k = 1, 8 , в Б(A) соответствует k -ый элемент множества E3 : {γ} соответствует (0, 0, 1) , {α, β} (1, 1, 0) и т. д.

Отметим следующее свойство булеана:

Б(A B) = {A1 B1|A1 Б(A), B1 Б(B)}.

10